Problem 1:

For the purpose of this problem, consider the m^- to be a heavy electron.

(a)  Find the normalized wave function for a m^- - ³He⁺⁺ bound system in its ground state.
(The system consists of a m^- orbiting a ³He⁺⁺ nucleus.)

(b)  What is the ground state binding energy of this system in terms of the ground state binding energy of the hydrogen atom?

(c)  Compare <r> and <r²> for the ground state of the m^- - ³He⁺⁺ system and for the hydrogen atom.

(d)  If a nucleus consisting of A-Z neutrons and Z protons suddenly decayed into a nucleus of A-Z-1 neutrons and Z+1 protons, how would you find the probability that the electron will remain in the ground state in terms of |y₁₀₀>_before and |y₁₀₀>_after?

Given: m_p=938 MeV/c², m_e=0.5 MeV/c², m_m=207 m_e.

Problem 2:

Find the wave functions and energy levels of the three-dimensional isotropic harmonic oscillator
(a)  in spherical coordinates, and
(b)  in Cartesian coordinates.
(c)  Express the wave functions n_r=1, l=1, in spherical coordinates as a linear combination of the wave functions obtained in Cartesian coordinates.

Problem 3:

The wave function of a stationary state of a hydrogen atom is

,

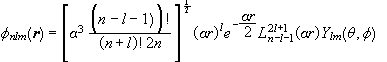where  .

The Laguerre polynomials are normalized in the following way:

.

Show that for any stationary state of a hydrogen atom the mean value of the kinetic energy is equal in magnitude and opposite in sign to the eigenvalue of the energy, i.e. E_n=-<p²/2m>_nlm.

Note: H=p²/2m-e²/r.

Problem 4:

For hydrogen-like atoms, such as the alkali atoms, the screening effect of the "closed-shell" electrons can be accounted for by considering the electron to move in the potential V(r)=-(e²/r)(1+a/r), where a is a constant.  Find the energy eigenvalues for this potential.