Problem 1:

The atomic orbitals of the electron in the hydrogen atom y_nlm(r)=R_nl(r)Y_lm(q,f) are eigenfunctions of H, L², and L_z.  Since the energy eigenvalue depends only on n, linear combinations of atomic orbitals with the same n, called hybrid orbitals, are also eigenfunctions of H.

(a)  Let n=2, l=1. Construct a basis of real wave function for the subspace E_n=2,l=1.  Discuss the angular dependence of these wave functions.

(b)  Construct two hybrid orbitals with the same geometrical form from y_2,0,0 and y_2,1,0.  Discuss their angular dependence.  Can you construct other orbitals with the same geometrical shape but different orientations by forming linear combinations of all atomic orbitals with n=2?

Problem 2:

Let m be the reduced mass of the nuclei of a H₂⁺ molecule and let m be the electron mass.  Let R denote the relative coordinates of the nuclei and r the electron's coordinates with respect to the center of mass of the nuclei.  Assume the center of mass of the nuclei is at rest.  Neglect spin.  Denote the potential energy of the electron in the field of the two nuclei by V(r,R).

(a)  Write down the eigenvalue equation for the Hamiltonian of the system.

(b)  Assume a solution of the form y(r,R)=c(R)f(R,r).  Which terms must be neglected for the time-independent Schroedinger equation to separate into

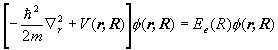
and

?

Problem 3:

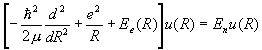The nuclei of a diatomic molecule are moving in a potential field given as

.

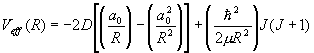Express this potential near its minimum by a harmonic oscillator potential and determine the vibrational energies of the molecule.

Problem 4:

Consider a particle of mass m in a central potential V(r)=-V₀, r<r₀, V(r)=0, r>r₀.  We may write any wave function f(r) of a particle in this potential as a linear superposition of partial waves of the form  .

(a)  Write down the differential equation for u_kl(r) and specify the boundary conditions at r=0, r=r₀, and r=¥ for a particle with energy E>0 and E<0.

(b)  For E<0 and l=0 find the equation that E has to satisfy in order for the differential equation to have a solution.

(c)  Assume that no bound state exists, i.e. the equation for E in part (b) has no solution. Solve the equation for u_k0(r) for a particle with E>0.
The asymptotic form of u_k0(r) is A sin(kr+d₀).  Assuming A=1, solve for both d₀, and the normalization constant of u_k0(r) in the region r<r₀.  Show that the normalization constant can be written as  with .

Note: sin²x = (1 + cot²x)^-1.

Problem 5:

Using spherical coordinates, obtain an expression for the probability current density j for the ground and excited states of the hydrogen atom.  Show in particular that for m_l ¹ 0 states there is a circulating flux in the sense that j is in the direction  of increasing or decreasing f, depending on whether m_l is positive or negative.