Problem:

The ground state wave function for a hydrogen like atom is

,

where  a₀ = ħ²/(μe²) and μ is the reduced mass, μ ~ m_e = mass of the electron. 
(a)  What is the ground state wave function of tritium?
(b)  What is the ground state wave function of ³He⁺?
(c)  An electron is in the ground state of tritium.  A nuclear reaction instantaneously changes the nucleus to ³He⁺.  Assume the beta particle and the neutrino are immediately removed from the system.  Calculate the probability that the electron remains in the ground state of ³He⁺.

Solution:

• Concepts:
  The hydrogenic atom, the sudden approximation
• Reasoning:
  Tritium and He⁺ are hydrogenic atoms.  Their wave functions and energy levels can be obtained from the wave functions and energy levels of the hydrogen atom using scaling rules.  We assume that right after the decay of tritium the wave function of the electron is the same as right before the decay.  It does not have time to change.  This is the sudden approximation.

• Details of the calculation:
  (a)  For a hydrogen atom we have
  .
  
  Defining
  ,
  we write
  .
  
  For a hydrogenic atom we have
  .
  
  .
  
  Defining
  ,
  we write
  .
  
  The same equations have the same solutions.  To find the eigenfunctions and eigenvalues of the Hamiltonian of a hydrogenic atom we therefore replace in the eigenfunctions of the Hamiltonian of the hydrogen atom   , and in the eigenvalues of the Hamiltonian of the hydrogen atom we replace  .
  (a)  Tritium:  The reduced mass is
  ,
  assuming the neutron mass equals the proton mass.
  The nuclear charge is Z = 1.  Since a₀' ~ a₀ the ground state wave function of the tritium is the ground state wave function of the hydrogen atom.
  .
  (b) ³He⁺:  The reduced mass is
  ,
  assuming the neutron mass equals the proton mass.
  The nuclear charge is Z = 2.  Since  a₀' ~ a₀/2 the ground state wave function of the ³He⁺ is
  .
  (c)  Sudden approximation:
  
  .
  .

Problem:

A negative K meson with mass m=1000 electron masses is captured into a circular Bohr orbit around a lead nucleus (Z=82).  Assume it starts with principal quantum number n=10 and then cascades down through n=9,8,7,... etc.

(a)  What is the energy of the photon emitted in the n=10 to n=9 transition?
(b)  What is the approximate radius of the lead nucleus if no further quanta are observed after the n=4 to n=3 transition (because of nuclear absorption of the K meson)?

• Solution:

  We have a hydrogen like system with Z=82:

  • (a)  .

    .

    .

  • (b)  The radius of Bohr orbits is .

    .

    This is the approximate radius of the lead nucleus.

    ,

    for Z=1.

Problem:

An electron in the n = 2, l = 1, m = 0 state of a hydrogen atom has a wave function ψ(r,θ,φ) proportional to r exp(-r/(2a₀)) cosθ, where a₀ is the Bohr radius.
(a)  Find the normalized wave function ψ(r,θ,φ).
(b)  Find the probability per unit length of finding the electron a distance r from the nucleus.
(c)  Find the most probable distance R_MP of the electron from the nucleus.
(d)  Find the average distance <r> from the nucleus.

Solution:

• Concepts:
  The fundamental assumptions of Quantum Mechanics
• Reasoning:
  If the wave function is normalized, then |ψ(r,t)|² is the probability density.
  The expression for the mean value of any observable A in the normalized state |ψ> is <A> = <ψ|A|ψ>. 

• Details of the calculation:
  (a)  Normalization:
  . 

  .

  .  .

  .

  (b)  P(r,θ,φ)d³r = |ψ(r,θ,φ)|²d³r  is the probability of finding the electron in an infinitesimal volume d³r about r = (r,θ,φ).  P(r,θ,φ)  is the probability per unit volume.

  

  P(r) is the probability per unit length.

  .

  (c)   We are looking for the maximum in P(r).

  

  (d)   _0.

Problem:

Find the momentum space wave function Φ(p) for the electron in the 1s state of the hydrogen atom.

Solution:

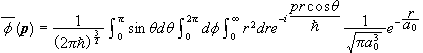
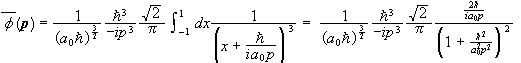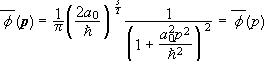• Concepts:
  Change of representation, the Fourier transform
• Reasoning:
  We are asked to change from the r to the p representation.
  Φ(r) = (2πħ)^-3/2∫_-∞^+∞ d³p Φ(p)exp(i(p/ħ)∙r),
  Φ(p) = (2πħ)^-3/2∫_-∞^+∞ d³r Φ(r)exp(-i(p/ħ)∙r),
  Φ(r) and Φ(p) are Fourier transforms of each other.
• Details of the calculation:
  The 1s wave function is
  .
  Therefore
  .
  Symmetry demands that Φ(p) = Φ(p).
  Let us choose a convenient direction for p.  Let p = pk.  Then

  

  

                                        

  .

  .