The simplest molecule possible is the H₂⁺ molecular ion.  It consists of two protons and one electron.  Assume that you could arbitrarily fix the distance between the protons.  When the distance between the protons goes to infinity then they do no longer interact.  The ground state energy of the system will be -13.6 eV, when the electron forms a hydrogen atom with one of the protons.  When the distance between the protons is on the order of nuclear dimensions then the electron will see a nucleus of charge Z=2.  The binding energy of the electron in the ground state will be -54.4 eV, the binding energy of the electron in the He⁺ ion.  The electron will be more strongly bound, but the protons will also repel each other strongly, so that the total energy of the system will be positive.  As the distance between the protons is varied, the total energy of the ground state reaches a minimum for a certain value of the distance.  This explains the stability of the H₂⁺ molecular ion.

In order to treat the problem exactly, one must solve the eigenvalue equation of the three particle system.  However, it is possible to simplify the problem by using the Born-Oppenheimer approximation.  The mass of the electron is much smaller than the mass of the protons, therefore the electron moves much more quickly than the protons.  The electronic wavefunction adapts itself nearly instantaneously to any change in the inter-nuclear distance r.  At any inter-nuclear distance r the Hamiltonian describing the nuclear motion therefore contains the terms associated with the kinetic energy of the nuclei, the nucleus-nucleus interaction, and the total energy of the electron at that inter-nuclear distance.  The nuclei move in an effective potential

  .

To find E_electron(r) the eigenvalue equation of the Hamiltonian of the electron, subject to the attraction of two fixed protons, must be solved.  The distance r between the protons is treated as a parameter, not as a quantum mechanical variable.  For the H₂⁺ molecular ion this eigenvalue equation can be solved exactly by choosing appropriate coordinates.  If the inter-nuclear axis is the z-axis, then we have already shown that L_z and the parity are good quantum numbers, but that L² is not a good quantum number for the energy eigenstates. (See notes.)  For other diatomic molecules with more than one electron, approximation methods must be used.  But for all stable diatomic molecules we find that has a minimum at a certain value of the inter-nuclear distance r.  V_eff(r) for is H₂⁺ shown in the figure below.

Motion of the nuclei

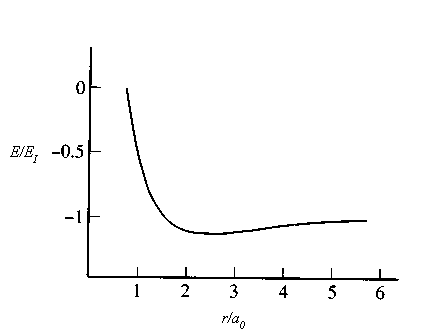
For a general diatomic molecule we want to solve the problem of two nuclei of mass m₁ and m₂ in a potential V_eff(r).  There exist vibrational and rotational degrees of freedom.  These degrees of freedom are coupled. When the molecule vibrates, its moment of inertia changes because the inter-nuclear distance r changes and therefore the rotational energy is modified.

Let us first consider only small amplitude vibrations.

The eigenvalue equation of the Hamiltonian for the relative motion of the two nuclei is

 ,

where m is the reduced mass, .

If the angular momentum of the nuclei is zero, then the eigenvalue equation reduces to the radial equation with l=0,

.

Let us expand V(r) about the equilibrium position r=r_e.

.

For small r’=r-r_e we have

,

or

.

This is the eigenvalue equation of a one-dimensional harmonic oscillator Hamiltonian.  The eigenvalues are

and we therefore have for the eigenenergies of the vibrational motion of the two nuclei

.

Typical vibrational frequencies are on the order of 10¹² to 10¹⁴ Hz and fall in the infrared.

The ground state wavefunction of the harmonic oscillator has a finite spread on the order of  .  (See notes.)  If , then the moment of inertia is nearly constant and to a good approximation the vibrational and rotational degrees of freedom are decoupled.

Heteropolar molecules, composed of two different atoms, generally have a permanent dipole moment p(r), because the electrons are attracted more towards one of the atoms.  We may expand p(r) as a function of the inter-nuclear distance, .  The energy of a charge distribution localized near the origin in an external field is given by .  This expansion shows the characteristic way the various multipoles of the distribution interact with an external field.  An external oscillating electric field therefore perturbs the Hamiltonian.  The eigenstates of the perturbed Hamiltonian may be written as linear combinations of eigenstates of the unperturbed Hamiltonian.  If at t=0 the system is in state |n>, then the probability that at some later time it can be found in the state |n’> will be proportional to |<n’|(r-r_e)|n>|². (See notes.)  Since r-r_e=r’ has a non-zero matrix element only between states for which , we only observe infrared absorption and emission at one Bohr frequency, .  (Higher order terms due to the anharmonicity of the potential are observed, but are much weaker.)

Homopolar molecules, consisting of two identical atoms, are inactive in the infrared.  The Hamiltonian for the nuclear motion is not perturbed by the oscillating electric field, because the charge distribution has no permanent dipole moment.  However the Hamiltonian for the electronic motion is perturbed, and therefore the molecule can acquire an induced dipole moment.  If the frequency of the oscillating electric field lies in the optical range transitions between electronic states can be induced.  Photons of energy can be absorbed and reemitted.  This phenomenon is called Rayleigh scattering.  If during the scattering a transition between occurs, then the energy of the scattered photon will be .  We therefore can observe scattered photons of three different frequencies.

( Rayleigh line ),
( Raman-Stokes line ),
( Raman-anti Stokes line ).

This can also be observed with heteropolar molecules.

Let us now study the rotational motion of molecules.  We neglect vibrations and assume that the distance r between the nuclei remains constant.  We then have a rigid rotator. (See notes.) We have

.

The eigenfunctions of H are the eigenfunctions of L².  These are the spherical harmonics, . The eigenvalues are . It is customary to set , and write .  The separation between adjacent levels is

,

it increases linear with l.  Each energy eigenvalue is (2l+1) fold degenerate.

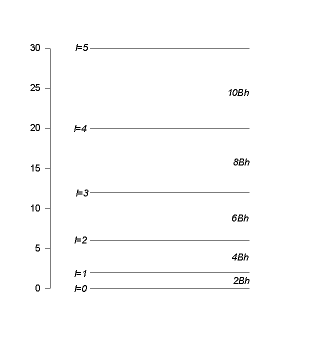
If a heteropolar molecule with a dipole moment p is placed in an oscillating electric field , the probability that the field induces a transition from an eigenstate of the rotational Hamiltonian |l,m> to the eigenstate |l’,m’> is proportional to .

With , the matrix element is proportional to

.

With

we have

.

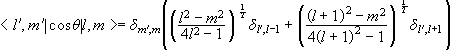The selection rules are .  For polarization of the electric field along the x- and y-axis we find .  The pure rotational absorption and emission spectrum is therefore composed of a series of equidistant lines.  The frequency separation between two successive lines is 2B.  Pure rotational spectra fall in the very far infrared or the microwave region.

Homopolar molecules which have no permanent dipole moment are inactive in the microwave region.  However, like the vibrations, the rotation of the molecule can be observed via the Raman effect in the inelastic scattering of light by the molecule.

Vibrational-rotational levels of diatomic molecules

In the Born-Oppenheimer approximation we assume that the potential energy of interaction between the two nuclei depends only on the inter-nuclear separation r.  The relative motion of the two nuclei can therefore be described in terms of the motion of a fictitious particle of reduced mass m moving in a central potential.  The stationary state wavefunctions of this particle are of the form , where satisfies

.

We have .

For l=0 we have already solved the problem for small amplitude oscillations and obtained the purely vibrational energy levels of the molecule, .

For we approximate .  We assume that l is sufficiently small such that .  Variations in the centrifugal potential are of the order and are neglected just as anharmonic terms in V(r) are neglected.  Then satisfies the equation

,

which again is the eigenvalue equation of a harmonic oscillator.  We therefore have

.

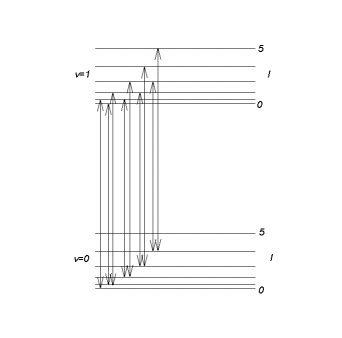
The radial functions do not depend on l, since does not depend on l.  The wave functions of the stationary states therefore are , with being a harmonic oscillator eigenfunction.  The first two vibrational levels with their rotational structure are shown in the figure below.

If a heteropolar molecule with a dipole moment p is placed in an oscillating electric field , the probability that the field induces a transition from an eigenstate of the vibrational-rotational Hamiltonian |n,l,m> to the eigenstate |n’,l’,m’> is proportional to .  With , the matrix element is proportional to

.

The selection rules for emission and absorption of infrared radiation therefore are   .

The set of lines with  constitutes a purely rotational spectrum.  For let n’ be the larger of the two vibrational quantum numbers.  Then we can separate the vibrational-rotational lines into two groups, .

For the frequency of the photon is given by

.

We observe the lines in the R branch of the figure below.

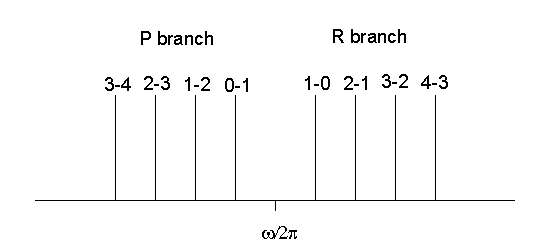
For the frequency of the photon is given by

.

We observe the lines in the P branch.  In each branch the distance between adjacent lines is 2B.  The central interval separating the two branches is of width 4B.  There is no line at the pure vibrational frequency . The pure vibrational spectrum consisting of a single line does not exist.  But with an instrument with poor resolution we may not be able to resolve the rotational structure and treat the band shown in the figure as a single line.

Links:

• Microwave and Infrared Spectra from Web Databases
• Vibrational-Rotational Spectrum Simulator
• Molecular Vibrations (in Spanish)