

The transition probability Pif(t,w) for an
atom placed into an electromagnetic plane wave with ![]() and angular frequency w near wfi is in the electric dipole approximation
and angular frequency w near wfi is in the electric dipole approximation
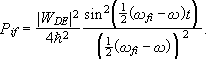
Here ![]()
The incident radiation, however is often not monochromatic. Let I(w)dw be the intensity of the radiation in the interval between w and w+dw. Assume the incident radiation is incoherent. Then
![]()
The total transition probability can now be found by integrating the transition probability induced by the radiation in each frequency interval.
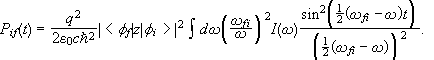
If I(w) varies little in the interval ![]() and
and ![]() then we may evaluate
then we may evaluate ![]() at
w=wfi and treat it
as a constant. We then obtain
at
w=wfi and treat it
as a constant. We then obtain
![]()
![]()
The transition probability per unit time is given by ![]() The transition probability per unit time
is proportional to the intensity of the radiation for induced
transitions.
The transition probability per unit time
is proportional to the intensity of the radiation for induced
transitions.
We can calculate induced transition probabilities using time-dependent perturbation theory, but as long as we treat the electromagnetic field classically, we cannot calculate the probability for spontaneous emission of a photon this way.
We can however avoid this problem by making statistical arguments. Consider two atomic states of energy E1 and E2. Let E2>E1. Assume the atom is bathed in radiation of energy density u(w). Transitions between these states can take place in three different ways.
A21, B21, and B12 are called the Einstein coefficients.
In a cavity in thermal equilibrium the probabilities that states 1 and 2 are occupied are exp(-E1/(KT)) and exp(-E2/(kT)) respectively, and in equilibrium the probability of up transitions must exactly balance the probability of down transitions. We therefore need
![]()
since B12=B21 is given by C12 from above, averaged over all polarizations and all directions of incidence of the plane wave.
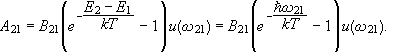
Since
we have
![]()
![]()
Use this information to derive the relations among Einstein's A and B coefficients which measure the spontaneous and the induced transition probabilities, respectively, between energy levels Ea and Eb.
(b) Now consider an atom in an electromagnetic field
![]()
with Hamiltonian
![]()
where -q is the charge of the electron.
The energy density
in the field is ![]() Neglecting terms in A2,
calculate the probability for absorption of radiation in the dipole approximation.
Express
your answer in terms of matrix elements of the form <b|r|a>.
Neglecting terms in A2,
calculate the probability for absorption of radiation in the dipole approximation.
Express
your answer in terms of matrix elements of the form <b|r|a>.
(c) Relate the lifetime of an excited state to the A coefficient and calculate the shape of the intensity distribution ( as a function of w ) observed as a consequence of spontaneous emission.
(a) ![]() (This was shown above.)
(This was shown above.)
(b) ![]()
![]()
The component of p in the direction of A commutes with A. A is perpendicular to the direction of propagation but depends on the coordinate in the direction of propagation.
![]()
![]()
![]() ( dipole approximation ).
( dipole approximation ).
![]()
![]()
Therefore
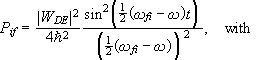
![]() with i = b and f = a.
(See previous module.)
with i = b and f = a.
(See previous module.)
This is what is required for part (b) of the problem. Let us expand and assume that the
incident radiation is not monochromatic. Let I(w)dw be the intensity of the radiation in the interval between w and dw.
Assume the incident radiation is
incoherent and ![]() Then
Then ![]() and the transition probability per unit
time is
and the transition probability per unit
time is
![]()
Let us expand even further and assume that the radiation is isotropic.
In order to find
the total rate induced by an isotropic field, it is necessary to sum this
expression over the two possible states of polarization for each direction of propagation
and to integrate over all directions of propagation. The two polarization vectors ![]() and the unit vector
and the unit vector ![]() form a triplet of orthogonal unit vectors.
For any fixed vector r we have
form a triplet of orthogonal unit vectors.
For any fixed vector r we have
![]()
![]()
Now let us relate I(wfi) to u(wfi) for the isotropic field. For a particular polarization
![]()
The factor of ½ is needed because u(w) contains two linearly independent polarizations. We now have
![]()
A21 is the spontaneous transition rate.
![]()
![]() is the lifetime,
is the lifetime, ![]()
Since the energies of excited states are not infinitely sharp, the emission lines have Lorentzian shapes. We write
![]()
Therefore
![]()