Identical particles

Consider two identical particles.  IF EÄE denotes the state space of the two particles and |ui,uj> a state vector in EÄE, then P21|ui,uj>=|uj,ui> must denote the same physical state, since we cannot distinguish the particles.  If |y> is a normalized state vector in EÄE then P21|y>=e|y>.  Since P212=I, e=±1.  Any physical state of two identical particles must be either symmetric or anti-symmetric with respect to the exchange of the particles.  Any physical state can be as a linear combination of basis vectors of the state space.  The state space of a two particle system therefore is not EÄE, but either the subspace or symmetric or the subspace of anti-symmetric states.  It is restricted.  This extends naturally to an N-particle system.

Postulate:

Every elementary particle is either a fermion or a boson.  A state of many identical particles is totally anti-symmetric if the particles are fermions, and it is totally symmetric if the particles are bosons.

Problem:

Fermions, bosons, and classical particles obey different probability laws.  Assume that two particles are placed at random into one of two boxes.  What are the probabilities of finding the following distributions?

Solution:
1.gif (1059 bytes) 2.gif (1067 bytes) 3.gif (1064 bytes)
Classical 1/4 1/2 1/4
Boson 1/3 1/3 1/3
Fermion 0 1 0

How do we construct a physical ket that correctly describes the physical state of a system of N identical particle?

Choose a basis for the single particle space E, for example the set {|uj>}.  Let the ket |y> in EÄEÄEÄ… be a tensor product vector, |y>=|ui>Ä|uj>Ä|uk>Ä….  Any vector in EÄEÄEÄ… is a linear combination of such tensor product vectors.
Apply S or A to |y>, depending on whether the particles are bosons or fermions.
Normalize the ket thus obtained to find |yS> or |yA>.

Examples:

Two bosons, one in a state |f> and one in a state |c>.

|y>=|f>Ä|c>.
S|y>=(1/2)(P12+P21)(|f>Ä|c>)=(1/2)(|fc>+|cf>).
<y|STS|y>=(1/4)(<fc|fc>+<cf|cf>)=1/2=1/N2.  N=21/2.
|yS>=(1/2)1/2(|fc>+|cf>).

Three bosons, one in a state |f>, one in a state |c> and one in state |w>.

|y>=|f>Ä|c>Ä|w>=|f,c,w>.
S|y>=(1/3!) åPa|y>
=(1/6)(|f,c,w>+|w,f,c>+|c,w,f>+|f,w,c>+|c,f,w>+|w,c,f>).
<y|STS|y>=(1/6)=1/N2.   N=61/2.
|yS>=(1/6)1/2(|f,c,w>+|w,f,c>+|c,w,f>+|f,w,c>+|c,f,w>+|w,c,f>).
If |f>=|c>=|w> then |y>=S|y>=|yS>=|f,f,f>.

Three fermions, one in a state |f>, one in a state |c> and one in state |w>.

|y>=|f>Ä|c>Ä|w>=|f,c,w>.
A|y>=(1/3!) åeaPa|y>
=(1/6)(|f,c,w>+|w,f,c>+|c,w,f>-|f,w,c>-|c,f,w>-|w,c,f>).
<y|ATA|y>=(1/6)=1/N2. N=61/2.
|yA>=(1/6)1/2(|f,c,w>+|w,f,c>+|c,w,f>-|f,w,c>-|c,f,w>-|w,c,f>).
If |f>=|c>=|w> then |y>=A|y>=|yA>=0.

Look at the definition of a determinant.

.

.

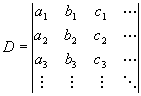eijk=+1 for even permutations, -1 for odd permutations.

We can therefore write

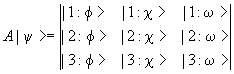1/N!.

A|y> is called a Slater determinant.  If any of the individual states |f>, |c>, and |w> are the same, then the determinant has two identical columns and therefore is zero.  We have the Pauli exclusion principle.

How do we find a basis for ES or EA?

{|yS>} or {|yA>} do not form a basis, because not all the vectors are linearly independent.

Example:

S|u1,u1,u2>=S|u1,u2,u1>= S|u2,u1,u1>.

Applying S to a basis of EÄEÄE we can obtain the same vector in ES more than once.  We introduce the occupation number nk of the individual state |uk>, equal to the number of times that state appears in the tensor product |ui>Ä|uj>Ä… .

.

Two different tensor product vectors, which have the same occupation numbers, are equal to each other within a factor of ±1 after applying S or A.  We denote the basis states by |n1,n2,n3,…,nk,..>, ånk=N.  For bosons the nk are arbitrary, subject only to the restriction ånk=N, for fermions nk=0, or nk=1.

Consequences of the indistinguishability on the calculations of physical predictions:

Consider two particles.  We know one is in the state |f> and one is in the state |c>.  The state of the two particle system is

|f,c>=|1:f,2:c> for distinguishable particles,
|f,c>=(1/2)1/2(1+P21)|1:f,2:c> for indistinguishable bosons,
|f,c>=(1/2)1/2(1-P21)|1:f,2:c> for indistinguishable fermions.

Let {|ui>} be an orthonormal basis of eigenvectors of some operator B.  B|ui>=bi|ui>.  What is the probability that a measurement of B yields bn for one particle and bn' for the other particle?

The eigenstate of B associated with this measurement is

|1:un,2:un'> or |1:un',2:un> for distinguishable particles,
|un,un'> =(1/2)1/2(1+eP21)|1:un,2:un'> for indistinguishable particles,
with e=1 for bosons
and e=-1 for fermions.

We therefore have for distinguishable particles,

P(bn,bn')=| <1:un,2:un'|1:f,2:c>|2+| <1:un',2:un|1:f,2:c>|2.

P(bn,bn') is the sum of the probabilities in of finding the particles in either of the two distinguishable states.

For indistinguishable particles there exists only one state |un,un'>,  and we have

P(bn,bn')=|(1/2) <1:un,2:un'|(1+eP21T)(1+eP21)|1:f,2:c>|2
=|<1:un,2:un'|(1+eP21)|1:f,2:c>|2
=|<un|f><un'|c>+e<un|c><un'|f>|2

(direct term           exchange term)

=|<un|f><un'|c>|2+|<un|c><un'|f>|2
+2e(Re(<un|f><un'|c>)Re(<un|c><un'|f>)+Im(<un|f><un'|c>)Im(<un|c><un'|f>)).
(interference terms)

Indistinguishability causes "interference terms" to appear when we calculate physical predictions.

If |un>=|un'>, bn=bn', then

P(bn,bn)=|<un|f><un|c>|2 for distinguishable particles,
P(bn,bn)=0 for indistinguishable fermions,
P(bn,bn=|<un|f><u'|c>+<un|c><un|f>|2
=2|<un|f><un|c>|2		 for indistinguishable bosons.