Consider the Helium atom.
(a) Write down the Hamiltonian in the central field approximation and the dominant correction term.
(b) What is the configuration of the ground, first excited, and second excited state?
(c) What type of splitting is introduced by the non-central part of the electron-electron interaction?  What is the degeneracy of each sublevel?
(d) What type of additional splitting is introduced by the spin-orbit interaction?

• Solution:

  (a) H₀=p₁²/(2m)+p₂²/(2m)-2e²/r₁-2e²/r₂+V_c(r₁)+V_c(r₂)
  is the Hamiltonian in the central field approximation.
  W =e²/r₁₂-V_c(r₁)-V_c(r₂)
  is the dominant correction term.  It is due to the non-central part of the electron-electron interaction.

  (b) The eigenvalues of H₀ depend on n₁, l₁ and n₂, l₂.

  • Configuration of the ground state: 1s²
  • Configuration of the first excited state: 1s2s
  • Configuration of the second excited state: 1s2p
  (c) The electron-electron repulsion term in the Hamiltonian commutes with L and S.
  [W, L₁]¹0, [W, L₂]¹0, but [W, L]=[e²/r₁₂, L]=0. [W, S]=0, where L=L₁+L₂, S=S₁+S₂.
  L and S are constants of motion.
  The anti-symmetric eigenfunctions of L², L_z, S², and S_z form an orthonormal basis for the subspace E_A(n₁l₁,n₂l₂).  The matrix elements of W between those basis vectors are diagonal and do not depend on M_L and M_S.  (W commutes with L_± and S_±.)  The eigenvalues of H therefore are E₀(n₁l₁,n₂l₂)+E₁(L,S). They are (2L+1)(2S+1)-fold degenerate.

  (d) The perturbation due to the spin orbit interaction may be written as

  .

  L_i is a vector operator in orbital space and S_i is a vector operator in spin space.  Within the subspace E_A(n₁l₁,n₂l₂,L) L_iµL by the Wigner-Eckart theorem, and within the subspace E(s₁,s₂,S) S_iµS.
  In the LS coupling scheme we therefore have W_soµL×S.
  L×S=(1/2)(J²-L²-S²)
  Inside each subspace E_A(n₁l₁,n₂l₂,LS) the eigenvalues of H depend on J and are (2J+1)-fold degenerate.

• Solution:

  (1s)² couples to L=0, S=0. (Pauli exclusion principle)
  (2s)² couples to L=0, S=0. (Pauli exclusion principle)
  The 2p and 3p electrons both have l=1, s=1/2. This can lead to L=2,1,0, S=0,1.

  We therefore can form the following terms:
  ¹D₂, ³D₁₂₃, ¹P₁, ³P₀₁₂, ¹S₀, ³S₁.
  

(a) Assuming LS coupling find L, S, and J values for the terms derived from the 4s² 3d and 3d 4s 4p configurations.  Write down each term in standard notation.

(b) Order the quadriplet terms of the 3d 4s 4p in order of increasing energy.  Order the levels of the 4D multiplet in order of increasing energy and indicate the relative spacing between levels of the multiplet.

(c) Write down dipole selection rules for LS coupling and indicate the allowed transitions.

(d) Which additional intersystem transitions are likely to occur?

• Solution:

  (a)

  	4s2	3d
  L	0	2
  S	0	1/2

  LS coupling: L=2; S=1/2

  Possible terms: ²D_5/2, ²D_3/2

  	3d	4s	4p
  L	2	0	1
  S	1/2	1/2	1/2

  LS coupling: L=3,2,1; S=3/2,1/2

  Possible terms: ⁴F_{9/2,7/2,5/2,3/2}; ²F_7/2,5/2,; ⁴D_{7/2,5/2,3/2,1/2}; ²D_5/2,3/2; ⁴P_5/2,3/2,1/2; ²P_3/2,1/2.

  (b)  Hund's rule: E_max to E_min
  ²P, ²D, ²F, ⁴P, ⁴D, ⁴F

  For the 4D multiplet: L×S=(1/2)(J²-L²-S²)=(J(J+1)-6-15/4)=(J(J+1)-39/4).

  	J=7/2	J=5/2	J=3/2	J=1/2
  (J(J+1)-39/4)	6	-1	-6	-9

   

  (c) LS coupling selection rule for allowed transitions:
  DL=±1, DJ=0,±1, DM_J=0,±1, DS=0.

  Ground state	ß   à	Excited state
  2D		2F
  2D		2P

   

  (d)  The next most likely transitions are magnetic dipole and electric quadrupole transitions.

  Magnetic dipole transitions:
  DL=0, DJ=0,±1, DM_J=0,±1, DS=0, no J=0 to J=0 transitions.

  Ground state	ß à	Excited state
  2D		2D

  Electric quadrupole transitions:
  DL=0,2, DJ=0,±1,±2, DM_J=0,±1,±2, DS=0.

  Ground state	ß à	Excited state
  2D		2D

The zeroth order Hamiltonian in jj coupling is given by

.

(a) What are the quantum numbers of the one-electron functions?

(b) What are the three jj coupling states that arise from (np)²?

(c) What are the possible j values for each of these states?

(d) What are the expectation values of the spin-orbit energy for each of these states expressed in terms of <np|a(r)|np>?

(e) What is the effect of introducing the electron-electron repulsion as a perturbation?  Sketch the transition from jj to LS coupling.

• Solution:

  (a) n,l,s,j,m

  (b) Configuration np²

  		possible terms
  np1/2 , np1/2	m1=1/2, m2=-1/2	(1/2,1/2)0
  np1/2 , np3/2	m1= ±1/2, m2= ±1/2, ±3/2	(1/2,3/2)2,1
  np3/2 , np3/2	m1=3/2, m2=1/2 m1=3/2, m2=-1/2 m1=3/2, m2=-3/2 m1=1/2, m2=-1/2	(3/2,3/2)2,0

  (c)  The possible values of J are

  • 0 for (1/2,1/2)_,
  • 2 and 1 for (1/2,3/2),
  • 2 and 0 for (3/2,3/2).

  (d) Both particles have the same n, l=1, and s=1/2. The allowed values for j₁, j₂ are (1/2,1/2)_, (1/2,3/2), (3/2,3/2). For indistinguishable particles the state vector must be anti-symmetric.

  |y_A>=(2)^-1/2(|j₁m₁;j₂m₂>-|j₂m₂;j₁m₁>)

  W_so=a(r₁)2l₁×s₁/+ a(r₂)2l₂×s₂/=W'(1)+W'(2).

  The matrix elements of W' are
  < jm_j|W'| jm_j'>= <nlsjm_j| a(r)(j²-l²-s²)| nlsjm_j'>=
  (j(j+1)-2-3/4) )<nlsjm_j| a(r)| nlsjm_j'>.
  The matrix elements are zero if m_j¹m_j'.

  We therefore have
  <y_A|W_so|y_A>=(1/2)(< j₁m₁|W'| j₁m₁>+< j₂m₂|W'| j₂m₂>)2.
  All the cross terms are zero since either j₁¹j₂ or m₁¹m₂.

  We have

  • <y_A|W_so|y_A>=2<np|a(r)|np> for (3/2,3/2),
  • <y_A|W_so|y_A>=-1<np|a(r)|np> for (1/2,3/2),
  • <y_A|W_so|y_A>=-4<np|a(r)|np> for (1/2,1/2).

  (d)  The operator for the electron-electron interaction, is a scalar operator.  It does not commute with j_i=l_i+s_i but commutes with j=åj_i.  The non-zero matrix elements of any scalar operator A, <kjm_j|A|k'j'm'_j> must satisfy j=j' and m_j=m_j' and do not depend on m_j.

  The matrix elements of in the subspace of vectors (j₁,j₂) are diagonal between eigenvectors of J², (j₁,j₂)_J.

  

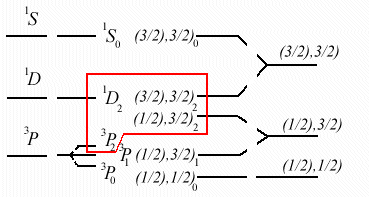
  In the transition, we match levels with the same value of J.

Consider a system of 4 identical particles.  Each particle has 3 possible eigenvalues, E₁, E₂, E₃, of some observable.

(a)    Use Young’s tableaux or any other method to find the number of possible states that are (i) symmetric, (ii) anti symmetric, and (iii) of mixed symmetry.

(b)    Write down the normalized symmetric wave function in which two of the particles have eigenvalue E₁, one has eigenvalue E₂, and one has eigenvalue E₃.

• Solution:

  Background :

  Young’s tableaux is a method of counting the number of states which are totally symmetric or anti-symmetric under the exchange of any two particles and the number of states with mixed symmetry.  States with mixed symmetry are symmetric or anti-symmetric under the exchange of some of the particles, but not all of the particles.

  Method:

  Each indistinguishable particle is represented by a box ([ ]), each of the possible states is represented by a number in that box (1,2,3,… ).

  • Example:
    A spin ½ particle can be in one of two possible eigenstates of S_z.  It is represented either by [1] (for spin up) or [2] (for spin down).

  A symmetric state of N particles is represented by a row of N boxes, an anti-symmetric state by a column of N boxes.

  For a row of N boxes, the numbers in the boxes cannot decrease when going from left to right, (n_i ³ n_i-1).  For a column of boxes , the numbers in the boxes must increase when going from top to bottom (n_j>n_j-1).

  • Example:

    For two spin ½ particles the possible symmetric states are [1][1], [1][2], [2][2], i.e. there are three symmetric states.  There is only one possible anti-symmetric state, .

  A tableaux for a mixed state has the following form:

  

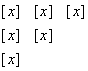
  i.e., the total number of boxes is N, and the number of boxes in row i must be less or equal the number of boxes in row i-1.  If the entries in the boxes of the tableaux T are labeled T_ij, the we need T_ij £ T_ij+1, T_ij < T_i+1j. (Rows are labeled by the index i, columns by the index j.)

  Why are we interested in mixed states?

  Assume the state space E=E(1)ÄE(2) is a tensor product space and we want to find the number of totally anti-symmetric states in E.  Product states which are products of a state symmetric in E(1) and a state anti-symmetric in E(2) or a state symmetric in E(2) and a state anti-symmetric in E(1) are obviously totally anti-symmetric in E.  But we also can find states totally anti-symmetric in E by combining mixed tableauxs.

  ---

  (a)  To find the number of symmetric states we count the number of rows we can form with four boxes (particles) and three numbers (states).

  Table 1

  P1	P2	P3	P4
  			1
  		1	2
  			3
  	1	2	2
  			3
  		3	3
  1		2	2
  	2		3
  		3	3
  	3	3	3
  		2	2
  	2		3
  2		3	3
  	3	3	3
  3	3	3	3

  
  We can form 15 symmetric states.

  There are no anti-symmetric states since we cannot form a column with four boxes (particles) and three numbers (states).

  We can form a mixed state by adding a box to a column with 3 entries
  (3 possibilities for [x]).

  

  or adding a box to a row with 3 entries.

  

  Referring to table 1, we have 6 rows beginning with 1.  For these rows y can be 2 or 3.  We have 3 rows starting with 2.  For these rows y can only be 3.  We therefore have 6+6+3=15 possibilities.

  We can also form a mixed state by forming a square.  There are 6 possibilities to form a square.

  

  The total number of mixed states therefore is 24.

  (b)  We find the sum of all possible permutations and divide by the square root of the number of permutations.
  |y>=[ |1,1,2,3>+|1,1,3,2>+|1,2,1,3>+|1,2,3,1>

                   +|1,3,2,1>+|1,3,1,2>+|2,1,1,3>+|2,1,3,1>

                   +|2,3,1,1>+|3,1,1,2>+|3,1,2,1>+|3,2,1,1>]/(12)^½ .