The total angular momentum J of an isolated physical system is a constant of motion.  This is a consequence of the isotropy of space.  Consider two angular momentum operators J₁ and J₂. J₁ operates in E₁ and J₂ operates in E₂.  Let J=J₁+J₂. J operates in E=E₁ÄE₂.

Examples:

Let J₁=L be the orbital angular momentum of a single particle and let J₂=S be its spin.  Then J=L+S. Or, let J₁=L₁ be the orbital angular momentum of one spinless particle and let J₂=L₂ be the orbital angular momentum of a second spinless particle.  Then J=L₁+L₂.

By showing that [J_i,J_j]=e_ijkJ_k we show that J=J₁+J₂ is an angular momentum operator.  For example,

The operator J² is  , since [J₁,J₂]=0.  We may write

=.

Since J is an angular momentum operator, [J²,J_i] = 0.

J² commutes with J₁² and J₂².

J_z commutes with J₁² and J₂².

J_z commutes with J_1z and J_2z.

However J² does not commute J_1z and J_2z.

Since the operators J₁², J_1z, J₂², and J_2z all commute, a basis of common eigenvectors for E exists.  We denote this basis by {|j₁,j₂;m₁,m₂>}.  Since the operators J₁², J₂², J², and J_z all commute, a basis of common eigenvectors for E exists.  We denote this basis by {|j₁,j₂;j,m>}.  We can write the vectors of one basis as linear combinations of the vectors of the other basis.
How do we find the right linear combinations?

Let us first consider a system of two spin ½ particles.  Let E_s=E_s(1)ÄE_s(2) be the state space of a system of two spin ½ particles.  The tensor product vectors {|++>,|+->,|-+>,|-->} form the {|½,½;m₁,m₂>} basis for E_s.  The common eigenvectors of S²=(S₁+S₂)² and S_z=S_1z+S_2z also form a basis of E_s, which we denote by {|S,S_z>}, where denotes the eigenvalue of S² and denotes the eigenvalue of S_z.

We have the singlet state

and the triplet states

.

These vectors form the {|½,½;j,m>} basis for E_s.  For the system of two spin ½ particles we therefore already know to write the vectors of one basis as linear combinations of the vectors of the other basis.

Problem:

• Solution:
  The common eigenvectors of S² and S_z form a basis for the vector space E_s of the two electrons.  Each common eigenvector is uniquely specified by its pair of eigenvalues.  We denote these eigenvectors by {|S,S_z>}, where denotes the eigenvalue of S² and denotes the eigenvalue of S_z.  We have

  ,

                                     triplet states

  and

  .

          singlet state

  The total spin of the two particles is S=S₁+S₂.
  ,
  
  .
  In the four dimensional state space of the two particles S_iz and S_i² are product operators.

   etc.

  The matrix of any product operator A(1)ÄB(2) in a basis of tensor product vectors {|i(1)>Ä|j(2)>=|i,j>} is

  ,

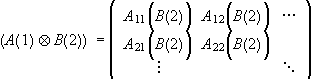  where the A_ij are the matrix elements of A in the {|i(1)>} basis of E₁ and is the matrix of B in the {|j(2)>} basis of E₂.

  Using the Pauli matrices,

  , , ,

  and we find the matrix of S_1z in the {|++>,|+->,|-+>,|-->} basis

  .

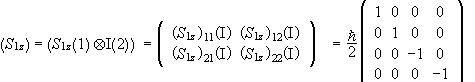  The matrix of S_2z is .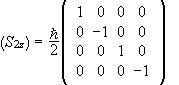

  The matrix of S₁² and S₂² is .

  In the {|++>,|+->,|-+>,|-->} basis we have

  .

  .

  .

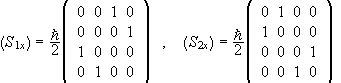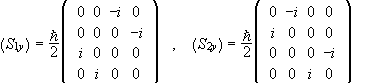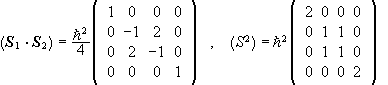  The matrix of S_z=S_1z+S_2z is 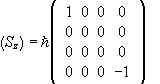in the {|++>,|+->,|-+>,|-->} basis.

  We now verify by matrix multiplication that the vectors,

  

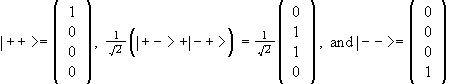
  are eigenvectors of S² with eigenvalue and of S_z with eigenvalue , respectively.

  ---

Let us now consider a system with arbitrary angular momenta J₁ and J₂.  Let {|k₁,j₁,m₁>} be a common eigenbasis of J₁² and J_1z in E₁, and let {|k₂,j₂,m₂>} be a common eigenbasis of J₂² and J_2z in E₂.  Then {|k₁,k₂;j₁,j₂;m₁,m₂>} is a common eigenbasis of J₁², J_1z , J₂², and J_2z in E₁ÄE₂.  We assume that k₁ and k₂ label the eigenvalues of some observables A₁ and A₂ that commute with J₁ and J₂, respectively.  We assume that {A₁,J₁²,J_1z} form a C.S.C.O. in E₁ and {A₂,J₂²,J_2z } form a C.S.C.O. in E₂. We may consider E₁ and E₂ to be the direct sum of subspaces E₁(k₁,j₁) and E₂(k₂,j₂), and consequently E(k₁,k₂;j₁,j₂)=E₁ÄE₂ to be the direct sum of subspaces obtained by taking the tensor product of E₁(k₁,j₁) and E₂(k₂,j₂). E₁(k₁,j₁) is the space of all vectors with the same values of j₁, i.e. the same eigenvalue Its dimension is 2j₁+1.  The dimension of E₂(k₂,j₂) is 2j₂+1 and the dimension of E(k₁,k₂;j₁,j₂) is therefore (2j₁+1)(2j₂+1).  E(k₁,k₂;j₁,j₂) is globally invariant under the action of any function of J₁ and J₂.  Operating with such an operator on a vector in E(k₁,k₂;j₁,j₂) yields another vector in E(k₁,k₂;j₁,j₂).

Since the operators A₁, A₂, J₁², J₂², J², and J_z all commute, {|k₁,k₂;j₁,j₂;j,m>} is also an eigenbasis for E.  We now want to express the vectors |k₁,k₂;j₁,j₂;j,m> in terms of the vectors |k₁,k₂;j₁,j₂;m₁,m₂>.  We therefore have to diagonalize the matrices of J² and J_z in the {|k₁,k₂;j₁,j₂;m₁,m₂>} basis.  Since E(k₁,k₂;j₁,j₂) is globally invariant under the action of any function of J² and J_z, these matrices are block diagonal.   Each submatrix corresponds to a particular subspace E(k₁,k₂;j₁,j₂).  Each vector |k₁,k₂;j₁,j₂;j,m> is a linear combination of vectors the |k₁,k₂;j₁,j₂;m₁,m₂ > with the same values of j₁ and j₂.  We only have to diagonalize inside each subspace, which has finite dimension (2j₁+1)(2j₂+1).  Inside each subspace the matrices of J² and J_z are independent of k₁ and k₂.  The diagonalization is the same inside all subspaces with the same j₁ and j₂.  We therefore simplify our notation and write E(k₁,k₂;j₁,j₂)=E(j₁,j₂) and |k₁,k₂;j₁,j₂;m₁,m₂>=|j₁,j₂;m₁,m₂> if we are only interested in the problem of adding angular momenta.

All vectors in E(j₁,j₂) with the same value of j, i.e. the same eigenvalue form a subspace E(j₁,j₂;j). Each E(j₁,j₂;j) is invariant under the action of J², J_z, J₊, and J_-.  We now want to know the possible values of j, given j₁, and j₂.

Assume j₁, and j₂ are given. Let Take a vector .

, m is uniquely determined by the values of m₁ and m₂.  The possible values for m are There are (2j₁+1)(2j₂+1) possible ways of obtaining m, since there are (2j₁+1) possible values of m₁ and (2j₂+1) possible values of m₂.  Certain values of m can be obtained in different ways, i.e. by adding different values of m₁ and m₂.

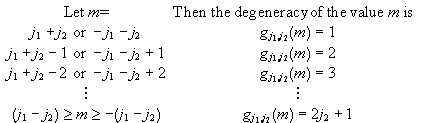
There are no values of m>j₁+j₂, therefore the maximum value of j=j₁+j₂.  There is only one eigenvector with m=j₁+j₂.  It is also an eigenvector of J² with j=j₁+j₂.

.  We can find the other eigenvectors with the same j by operating successively with J_-.

There are two vectors with .  Any linear combination of these two vectors is also a vector with .  Applying J_- we find that one particular linear combination is an eigenvector of J² with j=j₁+j₂.  The linear combination perpendicular to this one is an eigenvector of J² with j=j₁+j₂-1, it is the vector with j=j₁+j₂-1 and m=j₁+j₂-1.  Again we can find the other eigenvectors with the same j by applying with J_-.  Proceeding this way we find that the possible values of j are   A subspace E(j₁,j₂;j) of E(j₁,j₂) is associated with each of these values. E(j₁,j₂) is the direct sum of these subspaces.