The simplest model of a solid of volume V, for example a metal, is that of a potential box in three dimensions, filled with non-interacting electrons, i.e. a 3-dimensional, infinite square well.  The crystal structure is completely ignored.  For a cubic box with V=L³ the normalized energy eigenstates are the

The energy eigenvalues are

Problem:

(a)  Let the box contain one particle of mass M.  Determine (or write down) the general set of wave functions f(x,y), find the allowed energies for these states, and identify the eigenvalues k_x and k_y for the particle.

(b)  Sketch an energy level diagram for the lowest several states and write down the associated eigenvalues. Note the degeneracies, if any.

(c)  Make a plot, as a function of the eigenvalues k_x and k_y, showing the allowed states.  On this plot, consider a circle of radius k=(k_x²+k_y²)^1/2 with k large.  What is the area of this circle?  Approximately how many states are contained in this circle?

(d)  Now suppose that the same box contains N identical, non-interacting Fermi particles, each with mass M and spin ½.  We have N>>1.  Find the energy of the highest occupied state, if the system is in its ground state.

(e)  For the N particle system in part (d), calculate its total energy.

• Solution:

  (a) 

  

  (b) 

                               degenerate                                  degenerate

  c) 

  The area of a circle is A=pk². An area of (p/L)² is associated with each state.  The number of states in the circle is

  (d)  Each state can be occupied by two particles, one with spin up and one with spin down.  The energy of the highest occupied state is 

  (e)  The number of states between k and k+dk that can be occupied is  
  

  The total energy of the system is
  

  ---

In three dimensions the number of states in a sphere of volume (or the number of states with energy less than is

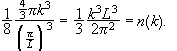
If we have N particles in their ground state in the cubic box, then where is the energy of the highest occupied state called the Fermi energy.

The number of states between k and k+dk is and the total energy of the filled Fermi sphere is

Therefore  Typical values of E_F in a metal are 5 to 10 eV.  At absolute zero the electron gas is in its ground state, all energy levels less than E_F are occupied.  Classically we expect an energy gain of ~kT or ~0.03eV per electron at room temperature.  But only electrons having an initial energy near E_F can "heat up".  There are no available states for electrons with initial energies appreciably lower than E_F.  Therefore the electrons contribute very little to the specific heat of metals at room temperature.  Only the ions contribute to the specific heat.

To understand why some materials are good conductors while others are insulators, we have to invoke the effects of the crystal lattice structure on the energy levels of the electrons.  To get a feel for the problem let us consider the motion of an electron in a one-dimensional structure V(x+a)=V(x), and let us impose periodic boundary conditions.  Then commutes with the translation operator H and U(T_a) have common eigenfunctions.

We have If a periodic function, then is an eigenfunction of U(T_a).  The eigenfunctions of H have the same form.  This is called Bloch’s theorem, and wavefunction of the form are called Bloch functions.  If y(x) is known over any one cell of the periodic lattice then we can instantly calculate it for any other cell using We need to solve the Hamiltonian for only one cell.  The periodic boundary conditions require y(x+Na)=y(x), where N is the number of cells in the lattice.  We therefore need

Consider a one dimensional periodic potential of the form

V(x)=0 for 0<x<(a-b), V(x)=-V₀ for -b<x<0, and V(x)=V(x+a), for all x.

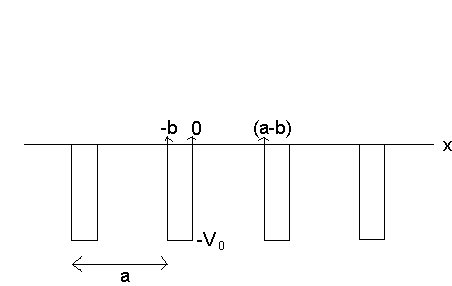
Defining the general solution of the time independent Schroedinger equation with E>0 (the particle is not trapped in a well) is

At x=0  are continuous.  Therefore

With we have

From  we obtain  or

and from we obtain

We may write

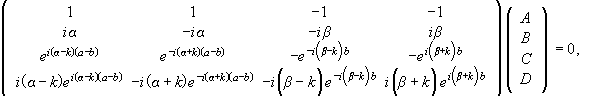
A nontrivial solution exists if det(M), the determinant of the above 4´4 matrix is zero.  After considerable algebra this yields the eigenvalue equation

Both contain E.  The right hand side of the equation is bounded between -1 and +1.  Therefore not all values of E are allowed, only those which make the left hand side also lie between -1 and +1.  This is the origin of the band structure in solids.  The allowed values are said to form the conduction bands, the values in between make up the forbidden bands.

Let us simplify the eigenvalue equation by letting b go to zero but the product bV₀ go towards a finite constant, i.e. by letting the width of the well go to zero while keeping the area constant.  Then bb goes to zero, but b²b remains finite.  In this limit the eigenvalue equation becomes

The left hand side may be written as

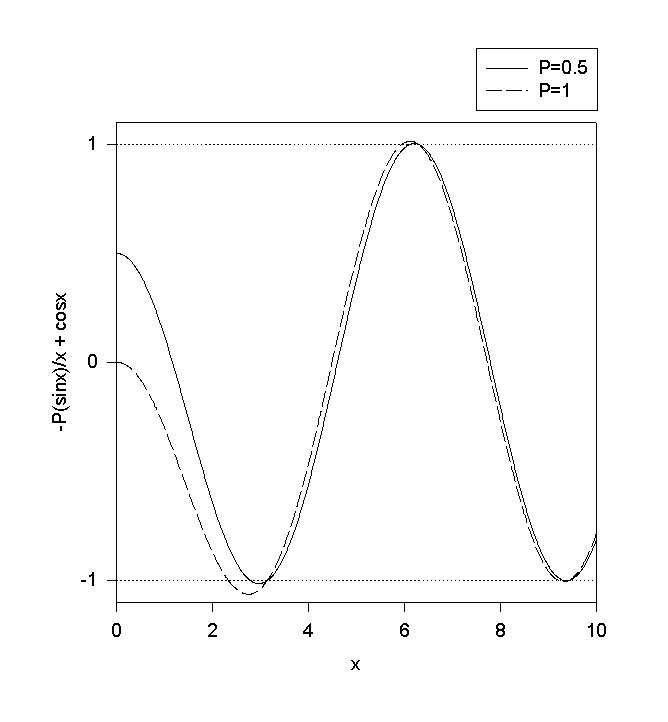
The graph shows plots of the left hand side for two different values of P.  When the plotted curves are outside the region between the dotted horizontal lines, the corresponding values of x (and E) are forbidden. We have a band gap.  Even though E>0, not all values of E are allowed.

A conductor happens when electrons partially fill a conduction band.  In this situation electrons can accelerate in response to an external electric field, since there are neighboring momentum states available.  An insulator consists of filled conduction bands.  Now there are no adjacent empty momentum states available, and the electrons cannot respond to an external electric field.

Links:

• Particle in a box
• Energy-band creator
• Periodic Potentials (in Spanish)