Assume the Hamiltonian of a system is

 ,

and the state vector of the system at t=t₀ is |y(t₀)>.  Then the state vector a time t is

The zero of the potential energy can be chosen arbitrarily.  Assume we add a constant V₀ to the potential energy.  Then the state vector a time t is

We have

This is a very simple example of a class of transformations, called gauge transformations.  There are no observable effects if every state vector in the world is multiplied by a common factor .  All matrix elements and expectation values remain unchanged.  Only phase differences are observable.  Our adding V₀ to the potential energy amounts to changing the total energy of the system, but only energy differences are observable.

Consider a particle in a uniform gravitational field.  The gravitational potential energy is mf_G, and the classical equation of motion is

The mass term drops out of the equation of motion.  In quantum mechanics the mass term no longer drops out. It appears in the combination .  We have

Does this lead to observable effects?
Ehrenfest’s theorem gives us the equation for the trajectory of the center of the wave packet describing the particle,

The combination does not appear here.  The appearance of in the Schroedinger equation does not lead to observable changes in the trajectory of a particle moving under the influence of gravity.  However, purely quantum mechanical effects are often observed through interference effects.

Problem:

• Solution:

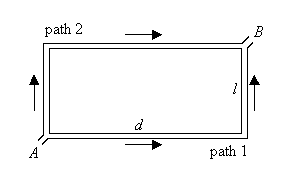
  If the neutrons were classical particles, then the time they would spend traveling from point A to point B along path 2 would be greater than the time they would spend traveling along path 1. In the horizontal section their speed would be lower when traveling along path 2 than when traveling along path 1.  If a neutron gun were shooting neutrons into the channel at point A at specific times, then we could determine which path a neutron took by measuring its time of flight to point B.

  In Quantum Mechanics, the uncertainty principle can prevent us from using time-of-flight techniques to determine the path.  We cannot determine the initial position and momentum, or the initial energy and entry time into the channel with arbitrary accuracy.  The uncertainty in the time of arrival at point B may therefore be larger than the predicted flight-time difference.

  Consider a steady stream of neutrons passing from A to B.  The Hamiltonian of the system is independent of time.  The eigenfunctions are therefore of the form y(r,t)=y(r)exp(-iwt).

  If path 2 is blocked the eigenvalue equation is H₁y₁(r)=Ey₁(r).  If path 1 is blocked the eigenvalue equation is H₂y₂(r)=Ey₂(r).  If both path are open we have Hy(r)=Ey (r).  We may write y(r)=ay₁(r)+by₂(r), where y₂(r) is zero if r lies along path 1 and y₁(r) is zero if r lies along path 2.  Let us choose a and b real.
  For simplicity, let us reduce the eigenvalue equation along each path to a 1-dimensional equation.  Then, using the WKB approximation, we at have at point B

  

  and

  ,

  where .

  At point B the phase difference between y₁ and y₂ is

  ,

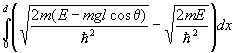
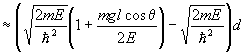  since the potential energy difference is much smaller than the total energy.

  Using E=p²/2m and p=h/l at point A, we have for the phase difference

  .

  With the phase difference betweeny₁ and y₂ being exp(iDf), the intensity at point B is given by

  .

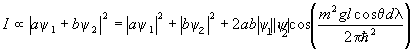  This effect has been observed.  For thermal neutrons with  we have As the apparatus is tilted from 0 to 90^o the intensity goes through a series of maxima and minima.  We observe approximately maxima.  (See Sakurai, page 129 and references therein, or the original paper: R. Colella, A. W. Overhauser, and S. A. Werner, Phys. Rev. Lett. 34 , 1472 (1975).)

  ---

Gauge transformations in electromagnetism

The Hamiltonian of a particle with charge e and mass m moving in an electromagnetic field is (in Gaussian units)

Here p is the canonical momentum of the particle, The mechanical momentum is  The electric and magnetic fields

,

are invariant under the gauge transformation

where f(r,t) is some scalar field.  Under a gauge transformation the Schroedinger equation,

,

becomes

If  then

and

and the original equation is restored.

For the Schroedinger equation to remain unchanged, the wave function y(r,t) must change into This corresponds to a phase change, which varies from one point to another, not a global phase factor.  For the state vector we have

In order for the behavior of an observable A to be invariant under a gauge transformation we need

A true physical quantity is an observable for which this is true.  The observable r is a true physical quantity.  For the observable p we have

G^TpG = G^TpG - G^TGp +p = G^T[p,G] + p

We used  

The canonical momentum p is gauge dependent and thus is not a true physical quantity.  However the mechanical momentum is gauge invariant. 

The Aharonov-Bohm effect

Suppose the magnetic field is in a cylindrical region of radius R and zero everywhere else.

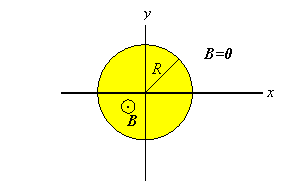
The vector potential A is not zero outside the cylindrical region. 

Assume the cylindrical region of radius R is inaccessible to a charged particle of mass m and charge e.  It never penetrates the region with the magnetic field.  Is the motion of the particle affected by the presence of the magnetic field?

If there is no field present, the Hamiltonian of the particle is

 ,

while in the presence of the magnetic field it is

If we write then the wave function y’ in the presence of the field is given in terms of the no field wave function y by

Here S denotes the path that the charged particle follows.  By following a path through a region where the field is zero but the vector potential is not zero the charged particle’s wave function acquires an additional phase

Again this phase change can be observed through interference effects.

Suppose a beam of electrons can reach a detector along two different path in a double slit experiment

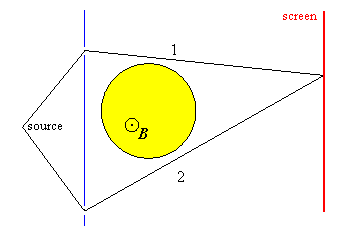
The additional difference in the phases of y₁ and y₂ is

.

Since

we have

Here F is the magnetic flux.  The additional phase difference displaces the interference pattern that is observed as a function of position on the detector.  This Aharonov-Bohm effect has been observed.  It is a purely quantum mechanical effect.  Classically the motion of the particle is determined by Newton's laws and the Lorentz force is zero in regions where B is zero.  In quantum mechanics the phase of the wave function depends on the vector potential A.  However the observable effects depend on phase differences, which in turn depend on the flux of the magnetic field B.  Observable effects have to be gauge invariant.

References:

• Y. Aharonov and D. Bohm, Phys. Rev. 115, 485 (1959)
• R. G. Chambers, Phys. Rev. Lett. 5, 3 (1960)

Link:

• The Aharonov-Bohm effect
• Aharonov-Bohm effect