The behavior of the cross section near a resonance

The Breit-Wigner resonance formula

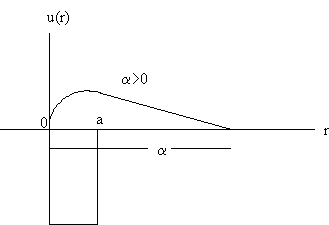
Consider low energy scattering off a square well potential, such that ka << 1 and only s-wave scattering is important.  At the resonance energy E_r, the phase shift δ₀ is π/2.
The scattering amplitude is
f_k(θ) = (1/k) exp(iδ₀) sinδ₀ = sinδ₀/(k exp(iδ₀)) = (1/k) sinδ₀/(cosδ₀ - isinδ₀).
The phase shift δ₀ is a function of E.  Near E = E_r let us expand sinδ₀ and cosδ₀.
sinδ₀(E) = sinδ₀(E_r) + cosδ₀(E_r)dδ₀/dE|_E=Er(E - E_r) = 1,
since cosδ₀(E_r) = 0 and sinδ₀(E_r) = 1.
cosδ₀(E) = cosδ₀(E_r) - sinδ₀(E_r)dδ₀/dE|_E=Er(E - E_r)
= -(E_r)dδ₀/dE|_E=Er(E - E_r) = -(2/Γ)(E - E_r)
with 2/Γ = dδ₀/dE.
Therefore, near E = E_r, we have
f₀ = (1/k) sinδ₀/(cosδ₀ - isinδ₀) = -(1/k)(Γ/2)/[(E - E_r) + iΓ/2].

The total cross section is now given by
σ_T = 4п|f₀|² = (4п/k²)(Γ²/4)/[(E - E_r)² + Γ²/4]

This is the Breit-Wigner resonance formula.  Γ is the width of the resonance curve.

Again, consider low energy scattering off a square-well potential, such that ka << 1 and only s-wave scattering is important   Assume that the potential has enough depth so that a bound state with a small  binding energy exists.

For this bound state we have
[(∂²/∂r²)  - U(r) - ρ²]u(r) = 0,  u(0) = 0,  u₂(∞) = 0,  ρ² = 2m|E|/ħ².
u₁(r) = A sin((U₀ - ρ²)^½r),  r < a.
u₂(r) = B exp(-ρr),  r > a.
At r = a we need hat u(r₀) and (∂/∂r)u(r)|_a are continuous.
A sin((U₀ - ρ²)^½a) = B exp(-ρa).
(U₀ - ρ²)^½A cos((U₀ -ρ²)^½a) = -ρB exp(-ρa).
Therefore cot((U₀ - ρ²)^½a) = -ρ/(U₀ - ρ²)^½.
Since E is small we replace (U₀ - ρ²)^½ with U₀^½ = k₀.
We then have
-ρ = k₀tan(π/2 - k₀a).

If k₀a is close to π/2, i.e. a bound state barely exists, we have -ρ/k₀ << 1, tan(π/2 - k₀a) << 1,
or, approximately,
-ρ/k₀ = (π/2 - k₀a),
k₀a = (π/2 + ρ/k₀).

Now let us look at a continuum state in the same potential.  For a low energy continuum state we have
tan(ka + δ₀) = (k/(k² + U₀)^½)tan((k² + U₀)^½a) .
Since k² << U₀ we approximately have (k² + U₀)^½a ≈ k₀a, and we write
k₀tan(ka + δ₀) =  k tan(k₀a),
or, making a connection with the bound state from above,
k tan(π/2 + ρ/k₀) = k₀tan(ka + δ₀) = k₀[tan(ka) + tan(δ₀)]/[1 - tan(ka) tan(δ₀)].

Now tan(π/2 + ρ/k₀) = -cot(ρ/k₀) = -1/tan(ρ/k₀) ≈ -k₀/ρ, since ρ/k₀ << 1.
We also have tan(ka) ≈ ka.
Therefore
-kk₀/ρ = k₀[ka + tan(δ₀)]/[1 - ka tan(δ₀)],
or
tan(δ₀) = k(aρ + 1)/(k²a - ρ),
or
k cot(δ₀) = -ρ/(aρ + 1) + ak²/(aρ + 1).

We write kcotδ₀ ≈ -ρ/(aρ + 1) + ak²/(aρ + 1) = -(1/α) + ½r₀k².
The quantity α is defined as the scattering length, and the quantity r₀ is defined as the effective range.
As k --> 0 we have kcotδ₀ --> -(1/α),  1/δ₀ --> -(1/αk),   δ₀ --> -αk,  f₀ --> -α,  σ_T --> 4πα². 
Since α = (aρ + 1)/ρ ≈ 1/ρ we we have established a connection between the energy of a bound state and the low-energy scattering cross sections for potentials that barely support one bound state.

At very low energy the Schroedinger equation for r > a becomes [(∂²/∂r²)u_k0(r) ≈ 0, and the asymptotic solution is a linear function of r. 
rΦ_k(r,θ,φ) = re^ikz + f_k(θ,φ) e^ikr --> r - α.
As k --> 0 we have rΦ_k(r,θ,φ) = 0 when r = α.  The scattering length can be interpreted as the r intercept of u_k0(r) since Φ_k(r,θ,φ) = 0 where u_k0(r) = 0.

Since 1/α = ρ/(aρ + 1) when k ≈ 0, and ρ = (2m|E|/ħ²)^½ we can infer the energy of a loosely bound state by performing a near zero energy scattering experiment.  Wigner first attempted to apply this to neutron-proton scattering.

Let us use what we know about the deuterium and try to predict the near zero energy scattering cross section.  With a binding energy of -2.23 MeV and a reduced mass of 940 MeV we find 1/ρ = 4.3*10^-15 m.  We have α =(ρa + 1)/ρ.  Taking a = 1.2*10^-15 m yields α = 5.5*10^-15 m and σ_T = 4*10^-24 cm².  The measured cross section however is σ_T = 20*10^-24 cm².  This discrepancy is mainly due to the spin dependence of the scattering cross section.  In the triplet state the neutrons scatter different than in the singlet state.  The bound state of the deuterium is the triplet state, the singlet state is not bound.  We should expect σ_T = (3/4)σ_t + (1/4)σ_s (statistical population).  Our prediction is for the triplet state.  For the singlet state we then expect σ_s = 4σ_T - 3σ_t =  68*10^-24 cm².  This is a huge cross section and it suggests a resonance.  The singlet state potential just misses to produce a bound state near zero energy.  The singlet state wave function u_k0(r) just misses to turn over and have a node and therefore the scattering length is large and negative.

Laboratory to center of mass frame transformations

We study the scattering of particles m₁ and m₂ with interaction energy V(|r₁ - r₂|) by studying the scattering of a fictitious particle of reduced mass  μ = m₁m₂/(m₁ + m₂)  by a potential (energy) V(r).  The vector r(r,θ,φ) describes the relative position of the two particles.  It points from particle 2 to particle 1.  The vector dr(r,θ,φ)/dt describes the relative velocity of the two particles, and its direction is the direction of the velocity of particle 1 in the CM frame.   We therefore calculate the cross section σ(θ,φ) in the CM frame of the two particles.  In most experimental situations, however, particle 1, with velocity v, approaches particle 2, at rest in the laboratory.  We measure the laboratory scattering angles θ₀ and φ₀ of particle 1.  We need the to relate the angles and the cross sections in the two frames.

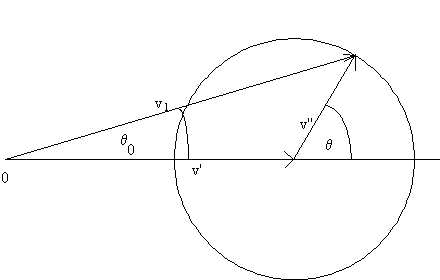
Let v’’ be the velocity of particle 1 in the center of mass frame, v₁ its velocity in the laboratory frame, and v’ the velocity of the center of mass frame with respect to the laboratory frame.  Then, as can be seen from the figure,

v₁cosθ₀ = v''cosθ + v',   v₁sinθ₀ = v''sinθ,  or  tanθ₀ = sinθ/(cosθ + γ).
Here γ = v'/v'' = m₁/m₂.  The ratio v'/v'' is equal to the ratio m₁/m₂.

[In the laboratory particle 1 approaches particle 2 with speed v. In the CM frame particle 1 approaches the CM with speed  v'' = m₂v/(m₁ + m₂) from the left and particle 2 approaches the CM with speed v' = m₁v/(m₁ + m₂) from the right.  Their relative speed is v and their total momentum is zero.  The speed of the CM in the laboratory is v’.]

The total number of particles scattered in to a detector is independent of the reference frame of the observer.
Therefore σ(θ₀,φ₀)dΩ₀ = σ(θ,φ)dΩ, 
σ(θ₀,φ₀) sinθ₀ dθ₀ = σ(θ,φ) sinθ dθ. 

We can therefore write
σ(θ₀,φ₀) = σ(θ,φ) sinθ dθ/(sinθ₀ dθ₀) = σ(θ,φ) dcosθ/dcosθ₀.

We have dtanθ₀/dcosθ₀ = (dtanθ₀/dcosθ) dcosθ/dcosθ₀.
But tanθ₀ = (1/cos²θ₀ - 1)^½.  We can therefore evaluate dtanθ₀/dcosθ₀.
Using tanθ₀ = sinθ/(cosθ + γ) we can evaluate dtanθ₀/dcosθ and therefore find dcosθ/dcosθ₀.

This then yields
σ(θ₀,φ₀) = σ(θ,φ) (1 + γ² + 2γcosθ)^½/|1 + γcosθ|.
We can now compare the cross sections measured in the laboratory frame with the cross sections calculated in the center of mass frame.

Dependence on γ

γ = m₁/m₂.  For γ < 1, m₁ < m₂, v’ < v’’, θ₀ increases monotonically from 0 to π as θ increases from 0 to π.  For γ = 1, v’ = v’’, θ₀ = ½θ and varies from 0 to π/2 as θ varies from 0 to π.  No particles appear in the backward direction. For γ > 1, m₁ > m₂, v’ > v’’, θ₀ increases from zero to a maximum value sin^-1(1/γ) as θ increases from 0 to cos^-1(-1/γ).  θ₀ then decreases to 0 as θ increases to π.  σ₀(θ,φ) is usually infinite at the maximum value of θ₀.  However this singularity gives a finite contribution to the total cross section.  No particles appear beyond the maximum value of θ₀ in the laboratory.  [In the figure the maximum value of θ₀ occurs when v₁ is tangent to the circle.]