Let H=H₀+H'=H₀+lW. Let {|fⁱ_p>} denote an orthonormal eigenbasis of H₀, H₀|fⁱ_p>=E₀^p|fⁱ_p>.  Here i denotes the degeneracy.  Consider a particular degenerate eigenvalue E₀^p of H₀.  Assume that this eigenvalue is g-fold degenerate, i=1,2,...,g.  To find E₁^p we use

Multiplying from the left by <fⁱ_p| we obtain

This is an eigenvalue equation for the operator W in the subspace E(0,p) of vectors with the eigenvalue of H₀ equal to E₀^p.  We find g eigenvalues E₁^p,i which may or may not be degenerate.  We then find the corresponding g eigenvectors.  To solve for the eigenvalues we set det(W-E₁^p)=0 in the subspace E(0,p).  If we find a non-degenerate eigenvalue E₁^p,i, then the corresponding eigenvector is uniquely defined.  If the eigenvalue E₁^p,i is degenerate then the corresponding eigenvector is still not uniquely defined.  The degeneracy may or may not be removed in higher order.

Assume that |c^j_p> is an eigenvector with eigenvalue E₀^p of H₀, but with a non-degenerate eigenvalue E₁^p,j. |c^j_p> is uniquely defined.  First-order perturbation theory has removed the degeneracy.  Let |y⁰_p>=|c^j_p>.

(H₀-E₀^p)|y_p¹> =( E₁^p,j-W)|y_p⁰> .

|y_p⁰> is an eigenstate of the unperturbed Hamiltonian.  We may expand

in terms of the basis vectors.

<y_p⁰|y_p¹> = 0.

Multiply from the left by <fⁱ_p''|.

We can solve for all bⁱ_p' but not for the bⁱ_p, they remain undetermined.  However, this does not preclude us from finding E₂^p,j , the second-order energy correction.

.

All the matrix elements multiplying the bⁱ_p are zero, since we have diagonalized the matrix of W.  Therefore, if first-order perturbation theory removes the degeneracy of a set of degenerate eigenvalues, we can proceed to find higher-order corrections to the now uniquely defined eigenvalues just like in the non degenerate case.

Problem:

q is the angular coordinate.  We have chosen units with

(a)   Find the complete set of eigenvalues and eigenfunctions of H₀.
(b)  Use perturbation theory to find the first and second-order corrections to the ground state energy E⁰ of H₀ due to the perturbation V for 0<a<½ .
(c)  For a=½ the ground state energy of H₀ is degenerate.  Find the first-order correction to E⁰ for this case.

• Solution:

  (a) 

  Try

  

   

  

   

  (b)  Let 0 < a < ½. Then all states are non degenerate and the ground state has n=0.

  

  

  

  

   

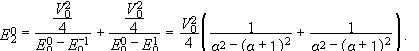
  (c)  If a=½ then all states are degenerate.  The ground state is any linear combination of n=0 and n=1. 

  We have to diagonalize the matrix of V in the subspace spanned by 

  

  

  

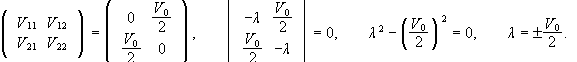
Links:

• Perturbation theory
• Perturbation theory
• Time-independent perturbation theory