Problem:

Find the ground state energy of the He atom using the variational method.

Solution:

• Concepts:
  The variational method
• Reasoning:
  We are asked to find the ground state energy of the He atom using the variational method.
• Details of the calculation:
  H = P₁²/(2m) + P₁²/(2m) - 2e²/r₁ - 2e²/r₂ + e²/r₁₂ = H₁ + H₂ + V₁₂.
  e² = q_e²/(4πε₀) in SI units.
  Let us use as a trial function  ψ(r₁,r₂) = (1/πa³)exp(-(r₁ + r₂)/a).
  We are guided by the ground state wave function of hydrogen, ψ(r) = (1/πa₀³)^½exp(-r/a₀).

  The adjustable parameter in our trial function is a = a₀/Z'. 
  ψ(r₁,r₂) is a product function, ψ(r₁,r₂) = Φ₁(r₁)Φ₂(r₂).
  Φ₁(r₁) = (1/πa³)^½exp(-r₁/a),  Φ₂(r₂) = (1/πa³)^½exp(-r₂/a).
  <ψ|H|ψ> = <Φ₁|H₁|Φ₁> + <Φ₂|H₂|Φ₂> + <ψ|V₁₂|ψ>.

• Φ₁(r₁) is the wave function of an electron in a hydrogenic atom with charge Z’.
  <Φ₁|p²₁/(2m)|Φ₁> = kinetic energy of an electron in a hydrogenic atom with charge Z’.
  <Φ₁|Z'e²/r|Φ₁> = potential energy of an electron in a hydrogenic atom with charge Z’.
  Therefore <Φ₁|H₁|Φ₁> = kinetic energy of an electron in a hydrogenic atom with charge Z’, plus 2/Z' times the potential energy of an electron in a hydrogenic atom with charge Z’.
  For an electron in the ground state of a hydrogenic atom with charge Z’ we have
  E_total = -Z²E_I,  2<T> = -<V>, (virial theorem)  E_total = T + V = -<T>.
  Therefore <T> = Z'²E_I,  <V> = -2Z'²E_I.
  Using our trial wave function we therefore have <Φ₁|H₁|Φ₁> = <Φ₂|H₂|Φ₂> = Z'²E_I - 4Z'E_I, and
  <ψ|H|ψ> =  2Z'²E_I - 8Z'E_I + <ψ|V₁₂|ψ>.
  <ψ|V₁₂|ψ> = (e²/(π²a⁶)) ∫∫d³r₁d³r₂ exp(-2(r₁ + r₂)/a)/|r₁ - r₂|
  = (5/4)e²/(2a) = (5/4)Z'E_I,  where E_I = e²/(2a₀).**
  <H> = 2E_I(Z'² - 4Z' + (5/8)Z').
  d<H>/dZ' = 0 --> 2Z' - 4 + 5/8 = 0.  Z' = 2 - 5/16 = 1.688.
  <H> = -2.85*2E_I = -77.5 eV.
  The experimental value for the ground state energy of He is -78.8 eV
  
  **How to evaluate the integral:
  We can recognize that the same integral can represent twice the electrostatic energy of a spherically symmetric charge distributions with charge density -q_eρ(r).
  Here ρ(r) = [1/(πa³)]exp(-2r/a).
  The electrostatic energy of such a distributions is
  U = (q_e/2)∫ρ(r)Φ(r)d³r = (e²/2)∫∫ρ(r)(ρ(r')/|r-r'|)d³rd³r'.
  The electrostatic energy of the charge distribution can also be found by evaluating a different integral.
  The electric field produced by the distribution is found from Gauss’ law.
  E(r) = E(r)(r/r),  E(r)4πr² = Q_inside/ε₀ in SI units.
  The self energy of the distribution is given by U = (ε₀/2 )∫₀^∞ E²(r)4πr²dr.
  Here
  Q_inside = -4πq_e∫₀^rρ(r')r'²dr' = (q_e/2)[2 - e^-x(x² + 2x + 2)], with x = 2r/a,
  U = (e²/8)∫₀^∞ [2 - e^-x(x² + 2x + 2)]²dr/r² = (e²/(4a))∫₀^∞ (2 - e^-x(x² + 2x + 2))²dx/x²,
  U = (e²/(4a)) 5/4.
  <ψ|V₁₂|ψ> = (5/4)(e²/(2a)).

  We can also evaluate the integral directly.  We write
  
  
  
  To carry out the angular integration we then use
  
  
  The integrals for the radial integration come straight out of common integral tables.

Problem:

Find the ground state energy of the He atom using the variational method.

Solution:

•  
  
  
  
   
  
  the ground state wavefunction for a hydrogenic ion with Z = 2.
  
  with
  
  
  
  The variational method often yields a very good estimate for the ground state energy of a system.  But an arbitrarily chosen trial ket can give a good approximation to the ground state energy but still be very different from the true eigenket.  So one must be very careful when using wave functions obtained by the variational method to calculate other physical quantities of the system.

Problems:

• Solution:

  

  The eigenfunctions of H must be zero at x=0 and x=¥. The derivative dy/dx must be continuous at all x except x=0.  Any function that satisfies these boundary conditions can be written as a linear combination of eigenfunctions of H and is an acceptable trial function giving <H>>E₀.
  We may choose as the trial function for x>0 the eigenfunction of the first excited state of the harmonic oscillator.  It satisfies the boundary conditions. We choose

  

  Note the change in the normalization constant, since we are only looking at x>0.

  

   

  since <T> = <V>.

  

   

  

  The exact solutions of

  

  or

   

  are the Airy functions y(z)=A_i(z), with boundary condition y(x=0)=0.

  

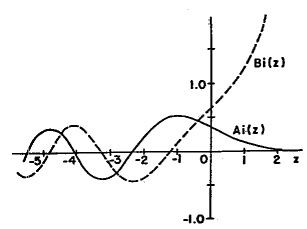
  x=0 Þ z=-E/(Fx₀). y(z) has its first zero at z=-2.338.

  

Calculate the splitting induced among the degenerate n=2 levels of a hydrogenic atom, when this atom is placed in a uniform electric field E pointing in the z-direction.  This is the linear Stark effect.  You may use the following explicit hydrogenic wave functions |nlm>:

and the fact that in general Hint: Exploit symmetries!

• Solution:

   

  The energy of the proton in the field is

  The energy of the electron in the field is

  The potential energy of both particles is

  Let us use first-order perturbation theory.

  The first excited state is 4-fold degenerate.

  

  To find E₁² we have to diagonalize the operator in the subspace spanned by |200>, |210>, |211>, and |21-1>.  The matrix elements between states with the same parity are zero.  This implies that all diagonal matrix elements are zero and all elements between states with the same l are zero.  The matrix elements between states with different m are zero. The only matrix elements left are <210|z|200> and <200|z|210>.

  

                                                 

   

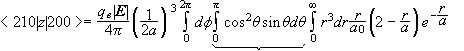
  We therefore have to diagonalize the matrix

  

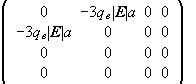
  in the |200>, |210>, |211>, |21-1> basis.

   

  

   (two fold degenerate ),

  or

  

  The eigenvectors corresponding to E₁²=0 are |211> and |21-1>.

  The eigenvector corresponding to E₁²=3q_e|E|a| is 

  The eigenvector corresponding to E₁²=-3q_e|E|a| is

  The four fold degeneracy is changed into two non degenerate eigenvalues and one two fold degenerate eigenvalue.