We have previously found the energy eigenvalues and eigenfunctions of the hydrogen atom, assuming that both the electron and the proton are point particles.  We then have used stationary perturbation theory to find corrections to the energy eigenvalues due to the finite size of the proton.  These corrections are extremely small.  We now want to use stationary perturbation theory to find corrections to the energy eigenvalues and eigenfunctions due to the spin of the electron and the proton, which we have neglected so far.

The electron is a spin ½ particle and has magnetic moment

with g = -2 and  in SI units.

The energy of this magnetic moment in a magnetic field B is W=-M_e×B.  In the rest frame of the electron the proton is orbiting the electron.  This moving charge produces a magnetic field at the position of the electron.  We might estimate the magnitude of this field by considering the orbiting proton to be a current loop of current I=q_e/t=q_ev/(2pr).  The magnetic field at the center of this current loop is

We therefore have, as an order of magnitude estimate only,

An order of magnitude estimate of the energy due to spin orbit coupling therefore is

where S and L are the spin and orbital angular momentum of the electron.  If <W_so> is small compared to then we can use perturbation theory to find corrections to the energy eigenvalues and eigenfunctions.

Let us find an order of magnitude estimate for <W_so>.  L and S are on the order of   <W_so> is on the order of   <H₀> is on the order of (Virial theorem: 2<T> = n<V>.)

is on the order of

r is on the order of  so 

So <W_so> is small compared to <H₀>.

In the hydrogen atom

So is on the order of v²/c².  It is of the same order of magnitude as are relativistic corrections to the kinetic energy.

We have

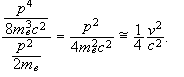
It therefore does not make much sense to correct the energy eigenvalues by including W_so and to neglect other correction terms of the same order of magnitude.  We must include all energy correction terms that are on the order of (v²/c²)H₀.  These terms produce the fine structure of the hydrogen atom.

The proton is also a spin ½ particle with a magnetic moment

In the magnetic field produced by the orbiting electron,

we estimate the energy of the proton to be

which is a factor of ~m_e/m_p smaller than W_so.

Because electron and proton both have magnetic moments, we expect another correction term to the energy due to the dipole interaction between the two magnetic moments.  This term is also on the order of ~m_e/m_p smaller than W_so.  Terms of this order produce the hyperfine structure of the hydrogen atom.

All these correction terms can be found from the Dirac equation for a spin ½ electron in the field of a stationary proton in the non-relativistic limit.