Self-consistent field approximation

The program hf.exe is a general Hartree-Fock program written by C. Froese Fischer, at Vanderbilt University.  It is written in FORTRAN, and has been compiled to run on a PC.  The source code is hf.for.  Input parameters must be entered exactly as indicated by the prompts.  The output file is hf.log.  By default, the single particle energies (in units of and the total energy (in atomic units of energy=) are written to this file.  To also write out the radial functions, do not choose default values for the remaining parameters, and then choose PRINT to be true.

The Hartree equations

Consider the Hamiltonian

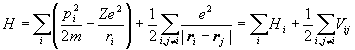
for an atom with Z electrons.  Assume that a solution in the form of a product of single-particle wave functions exists,

y(r₁,r₂,…,r_Z)=f₁(r₁)f₂(r₂)…f_Z(r_Z),

and that all the single particle wave functions are normalized.

.

Pick a trial function of the above form for a variational calculation.  Ask what type of single particle wavefunction minimizes .  We have

.

All the other coordinates integrate out.  Let us now minimize <H> with respect to variations df_i^*, with .

.

The equation, , acts as a constraint on the variations of <H>.  We handle it using the method of Lagrange multipliers.  We multiply each of the equations by e_i and then subtract the sum from <dH>.

.

Since the variations df_i^* are independent, the above equation cannot be satisfied unless the coefficients of each df_i^* vanish independently.  Therefore

.

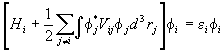This is the equation that the single particle wavefunction for the ith electron has to satisfy.  It is called the Hartree equation.  It is an eigenvalue equation for a single electron moving in the Coulomb potential of the nucleus plus a potential due to all the other electrons.  The potential due to the other electrons depends on the charge density e|f_j(r_j)|².  This charge density is only known after the above equations has been solved for each i.

The self-consistent field approximation is an iterative procedure for solving the above set of equations.  A trial function is used to calculate the initial charge density.  New single particle wave functions are found by numerically solving the above equations.  These wave functions now yield new charge densities, which in turn yield new wave functions.  The procedure is repeated until the single particle wave functions f_i and the single particle energies e_i do no longer change, i.e. until self consistency is reached.

The central-field, self-consistent field approximation consists of replacing by its average, averaged over all angles, making it a central potential.  Now the single particle wave functions are characterized by the quantum numbers (n,l,m,m_s)_i.

The total energy in the self-consistent field approximation is not the sum of the single particle energies e_i. This would double count the repulsive electron-electron interactions.  The total energy is found by substituting the final product wavefunction back into the equation for <H>.

Link:

• Herman-Skillman code for self-consistent field approximation calculations

The Hartree-Fock equations

The Hartree equation does not include electronic correlations introduced by the anti-symmetrization of the total wavefunction of a many-electron atom.  To derive the Hartree-Fock equations, anti-symmetric wave functions are introduced as Slater determinants.

y(r₁,r₂,…,r_Z)=(N!)^-1/2det(f_i(r_j))

If the Hamiltonian does not involve the electron spin, we may write f_i(r_i)=f_ai(r_i)|m_si>.  The equation for <H> now becomes

,

where

and

.

(1/2)òF(r)r(r)d³r is the direct term and the last term in the expression for <H> is the exchange energy.  It arises from anti-symmetry of the trial wavefunction.  As written above, both terms contain contributions from unphysical self-energies (i=j), but these contributions cancel each other out.

If we make the central field approximation then the single particle wave functions are of the form f_ai(r)=(u_nl(r)/r)Y_l(q,f), with ò|u_nl(r)|²dr=1.  We introduce the number of electrons in each subshell N_nl, and assume that the average angular distribution of these electrons is uniform.  (For each shell we average over all possible values of m and m_s.)  Then

, .

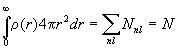Then

,

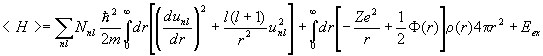with

.

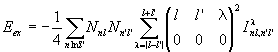Here I is the integral

,

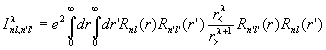and  is a 3j symbol.

Minimizing <H> with respect to variations on f_ai^* and introducing Lagrange multipliers yields the Hartree-Fock equation

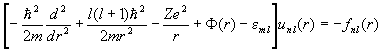
with

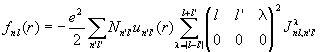
and

.

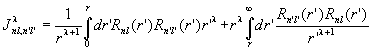The exchange energy has introduced a non-locality (Fock potential) embodied in f.  This non-locality couples together the eigenvalue equations for each of the radial wave functions.

Link:

• Foundations of Computational Chemistry And Material Science