Flux, Gauss' law
Flux
Problem:
A disk with radius r = 0.10 m is oriented with its normal unit vector
n
at an angle of 30o to a uniform electric field E with
magnitude 2.0*103 N/C.
(a) What is the electric flux through the disk?
(b) What is the flux through the disk if it is turned so that its normal is
perpendicular to E?
(c) What is the flux through the disk if its normal is parallel to
E?
Solution:
- Concepts:
Electric flux
- Reasoning:
The flux is given by Φ = ∫E∙dA.
- Details of the calculation:
(a) Since the field is constant, Φ = EAcosθ, where θ is the angle between the
field and the normal, and A = πr2 = π(0.1)2 = 0.0314 m.
Then for θ = 30o we obtain Φ = 54.4 Nm2/C.
(b) Now θ = 90o thus Φ = 0 Nm2/C.
(c) Now θ = 0o thus Φ = 63 N m2/C.
Gauss' law, spherical symmetry
A solid conducting sphere of radius 2 cm has a charge of 8 microCoulomb. A
conducting spherical shell of inner radius 4 cm and outer radius 5 cm is
concentric with the solid sphere and has a charge of -4 microCoulomb.
(a) What is the magnitude and direction of the electric field at r = 1 cm?
(b) What is
the magnitude and direction of the electric field at r = 3 cm?
(c) What is
the magnitude and direction of the electric field at r = 4.5 cm?
(d) What is the magnitude and direction of the electric field at r = 7 cm?
Similar problem:
Problem:
Inside a sphere of radius R and uniformly charged with the volume
charge density ρ, there is a
neutral spherical cavity of radius R1 with its center a
distance a from the center of the charged sphere. If (R1 + a) < R,
find the electric field inside the cavity.
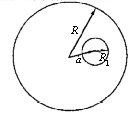
Solution:
- Concepts:
Gauss' law, the principle of superposition
- Reasoning:
We can view the sphere with the cavity as a superposition of a sphere with
radius R having a uniform charge density
ρ and another sphere with radius
R1 located in the cavity space having a uniform charge
density -ρ. The field due to each
of these spherical charge distributions can be found from Gauss' law.
- Details of the calculation:
Let the center of the large sphere be located at the origin.
E = E1 + E2.
E1 = ρr/3ε0
for r < R.
E2 = -ρ(r-a)/3ε0
inside the cavity.
Inside the cavity we therefore have E = ρr/3ε0
- ρr/3ε0
+ ρa/3ε0
= ρa/3ε0
The field inside the cavity is constant and points into the direction of the
vector a.
Problem:
The electrostatic potential V is 0 on a
spherical shell of radius r1 = 0.10 m and V is 100 Volts for a
concentric shell of radius r2 = 2.00 m. Assume free space between these
concentric shells, and find E between the shells.
Solution:
- Concepts:
Gauss' law
- Reasoning:
The problem has enough symmetry to find E(r) from Gauss' law alone.
-
Details of the calculation:
From Gauss' law: E(r ) ∝ 1/r2 between the spheres.
The direction of E is radially inward. E(r) = -A/r2, wit
A positive.
Then V0 = -∫r1r2E(r)dr = A∫r1r2(1/r2)dr
= -A(1/r2 - 1/r1) - 100 V
A(1/(0.1 m) - 1/(2m)) = 100 V.
A = (100/9.5) Vm.
E = -10.526 V/m (r/r).
Problem:
A charge distribution produces an electric field E = A(1 - exp(-βr))(r/r3)
where A and
β are constants. Find the net charge within the
radius r = 1/β.
Solution:
- Concepts:
Gauss' law
- Reasoning:
A radial field is produced by a spherically symmetric charge distribution.
- Details of the calculation:
E(r)4πr2 = Qinside/ε0
in SI units.
For r = 1/β we have A(1 - e-1)4π = Qinside/ε0.
Qinside = A(1 - e-1)4πε0.
Problem:
Determine the charge distribution that will give rise to the potential V(r)
= kq exp(-mr)/r, with m a positive constants. Calculate the total charge in the
distribution.
Solution:
- Concepts:
Gauss' law,
∇2V(r) = -ρ/ε0,
- Reasoning:
V(r) = V(r). ∇2V(r) = -ρ/ε0,
except at r = 0, where the expression for
∇2V(r) = is not defined.
To find the charge at the
origin we use Gauss' law.
- Details of the calculation:
∇2V(r) = (1/r2)(∂/∂r)(r2∂V(r)/∂r)
= m2 kq exp(-mr)/r = m2V(r) = -ρ/ε0,
except at r = 0, where the above expression for
∇2V(r) = is not defined.
To find the charge at the
origin we use Gauss' law.
E = -∇V(r)
= (∂V(r)/∂r)(r/r).
Er(r) = (kq/r2)exp(-mr) + kq m exp(-mr)/r.
For a spherical surface of radius r we have 4πr2E(r)
= Qinside/ε0.
As r --> 0, Qinside/ε0
= 4π kq.
The charge distribution that gives rise to the potential V(r)
= kq exp(-mr)/r therefore is
ρ(r) = 4πε0
kqδ(r) -
ε0m2 kq exp(-mr)/r.
With k = 1/(4πε0
) we have ρ(r) = qδ(r)
- (m2/4π)q exp(-mr)/r.
The total charge in the
distribution is given by
Q =
∫all space ρ(r)dV = q∫all space δ(r)dV - (m2/4π)q
4π ∫0∞
r2 exp(-mr)/r dr
= q - m2q/m2
= 0.
Problem:
(a) Consider a non-conducting sphere with radius a. This sphere carries a
net charge Q, assumed to be uniformly distributed. Find the electric field
inside and outside the sphere. Sketch the result.
(b) Now consider a conducting sphere with radius a carrying a net charge Q.
Find the electric field inside and outside the sphere.
Solution:
- Concepts:
Gauss' law, Φe = ∫closed surface
E·dA
= Qinside/ε0
- Reasoning:
The charge distribution has spherical symmetry and E can be found from Gauss'
law alone.
- Details of the calculation:
(a) Place the center of the sphere at the origin of the coordinate system.
Consider a spherical Gaussian surface of radius r centered at the center of the
spherical charge distribution.
i. Let r be greater than a, so that the surface encloses the entire charge
distribution.
The electric field is radial, the vector E is normal to any surface
element dA. Thus flux through the surface is Φe = ∫
E·dA
= ∫EdA = E 4πr2 = Qinside/ε0 = Q/ε0
E = Q/(4πε0r2)
n, where
n = r/r.
The field outside the sphere looks like the field of a point charge Q.
ii. Let r be smaller than a, so that the surface only encloses a part of the
charge distribution. Now Qinside is the charge density ρ = Q/V times
the volume 4πr3/3 of the distribution which lies inside the spherical
Gaussian surface. We therefore have
E = ρr/(3ε0)
n = Qr/(4πε0a3)
n.
The field inside the sphere increases linearly with r.
(b) The charge is uniformly distributed over the surface of the conductor.
r >a: E = Q/(4πε0r2)
n, r < a: E
= 0, the electric field inside a conductor is zero in electrostatics.
Problem:
A sphere of radius R has volume charge density ρ = Krn, for some
constants K and n. The region r > R is filled with a conductor (all the way to
infinity).
(a) Find the volume charge density ρ in the region r > R, inside the
conductor, and the surface charge density at r = R.
(b) Find the electric field E everywhere, i.e. for r < R and for r
> R.
(c) Find the potential Φ everywhere, taking Φ to vanish at infinity.
(d) How much energy is stored in this system?
- Concepts:
Gauss' law, properties of conductors
- Reasoning:
The problem has spherical symmetry. Inside a conductor ρ and
E are
zero.
- Details of the calculation:
(a) ρ = 0 in a conductor, and since E = 0, the total charge enclosed by a
Gaussian surface in a conductor is zero, so the surface charge at r = R
cancels that of the charged sphere.
σ = (1/(4πR2))∫00Krn
4πr2 dr = -KRn+1/(n + 3)
The surface charge is uniformly distributed on the inner surface of the
conductor.
(b) By symmetry E(r) = E(r)r/r. Gauss' law applied to
a Gaussian spherical surface of radius r < R gives
E(r)4πr2 = -4πKrn+3/((n + 3)ε0), E(r)
= -Krn+1/((n + 3)ε0), for r < R.
Again E = 0 for r > R, inside the conductor.
(c) Writing the above E as -∇Φ, we obtain
Φ = - K(rn+2 - Rn+2)/((n + 2)(n + 3)ε0)
for r < 0, Φ = 0 for r > 0.
(d) U = ½∫ρΦdV = (ε0/2)∫E2dV
= 2πK2R2n+5)/((2n + 5)(n + 3)2ε0)
Problem:
Two metallic spheres of the same radius r are immersed in a
homogeneous liquid with resistivity ρ.
What is the total resistance between two spheres? Assume that the distance
between two spheres is much larger than the sphere radius.
Solution:
Problem:
A charge Q is uniformly distributed through the volume of a sphere of radius
R. Calculate the electrostatic energy stored in the resulting electric field.
Solution:
- Concepts:
Gauss' law, electrostatic energy
- Reasoning:
A radial field is produced by a spherically symmetric charge distribution.
- Details of the calculation:
From Gauss' law we have E(r) = Q/(4πε0r2) for r > R, and
E(r) = ρr/(3ε0) for r < R.
Here ρ = 3Q/4πR3. Therefore E(r) = Qr/(4πR3ε0)
for r < a. At r = 0 we have E(r) = 0.
The total electrostatic energy of the sphere may be calculated from the electric
field, using U = (ε0/2) ∫all space E·E dV.
(SI units).
U = (4πε0/2)[∫0Rr2dr Q2r2/(4πR3ε0)2
+ ∫R∞r2dr Q2/(4πε0r2)2]
= (Q2/(8πε0))[∫0Rr4dr/R6
+ ∫R∞dr /r2] = [Q2/(8πε0)][1/(5R)
+ 1/R] = (3/5)Q2/(4πε0R).
Problem:
A model of the hydrogen atom was proposed before the advent of quantum
mechanics, which consists of a single electron of mass m and an immobile uniform
spherical distribution of positive charge with radius R. Assume that the
positive charge interacts with the electron via the usual Coulomb interaction
but otherwise does not offer any resistance to the motion of the electron.
(a) Explain why the electron's equilibrium position is at the center of
the positive charge.
(b) Show that the electron will undergo simple
harmonic motion if it is displaced a distance d < R away from the center of the
positive charge. Calculate its frequency of oscillation.
(c) How
big would the atom need to be in order to emit red light with a frequency of
4.57*1014 Hz? Compare your answer with the radius of the
hydrogen atom.
(d) If the electron is displaced a distance d > R from
the center, will it oscillate in position? Will it undergo simple harmonic
motion? Explain!
Solution:
- Concepts:
Gauss' law
- Reasoning:
The field due to a spherically symmetric charge
distribution can be found from Gauss' law.
- Details of the calculation:
The charge distribution is spherically
symmetric and so the electric field is E(r) = E(r)
r/r.
Let the center of the positive charge be the origin and consider a Gaussian
surface defined to be a sphere or radius r at the same origin.
The total
flux is Φ = ∫E·dA = 4πr2E(r) = Qinside/ε0.
If 0 < r < R, then Qinside = 4πρr3/3, with ρ = 3qe/4πr3.
In this region E(r) = ρr/(3ε0).
If r > R, the electric field
is the same as expected for a point charge, E(r) = qe/4π ε0r2.
We can now easily answer the questions.
(a) The force acting on the
electron is F(r) = -qeρr/(3ε0), pointing towards the
origin. Therefore the only point where the sum of all forces is zero is the
origin.
(b) The force is a restoring force and is proportional to the
displacement of the electron from r = 0. The resulting motion will be
simple harmonic motion.
The "spring constant" associated with this
motion is k = qeρ/(3ε0) = qe2/(4πε0R3).
The frequency of the oscillations is therefore
f = (2π)-1(k/m)1/2
= (2π)-1(qe2/(4πε0mR3))1/2.
(c) R = [qe2/(16π3ε0mf2)]1/3.
For f = 4.57*1014 Hz we need R = 3.13*10-10 m.
(d) For d >
R the force is still restoring. Therefore the electron will undergo
oscillatory motion. The magnitude of the force is proportional to 1/r2,
however, and therefore the motion will not be simple harmonic motion.
Problem:
A spherical charge distribution is given by
ρ = ρ0(1 - r/a),
r < a,
ρ = 0, r > a.
(a) Calculate the total
charge Q.
(b) Find the electric field and potential for r > a.
(c)
Find the electric field and potential for r < a.
(d) Find the
electrostatic energy of this charge distribution.
Solution:
- Concepts:
Gauss' law
- Reasoning:
The field due to a spherically symmetric charge
distribution can be found from Gauss' law.
- How do they apply?
(a) Q = 4πρ0∫0a
r2dr(1 - r/a) = 4πρ0[(a3/3) - (a3/4)]
= 4πρ0a3/12.
(b) E = (1/(4πε0))Q/r2,
radially outward for positive ρ0.
E = (1/ε0)ρ0a3/(12r2).
Φ = (1/(4πε0))Q/r = (1/ε0)ρ0a3/(12r).
(c) E = (1/(4πε0)) Qinside/r2, radially
outward for positive ρ0.
Qinside = Q = 4πρ0∫0r
r'2dr'(1 -r'/a) = 4πρ0[(r3/3) - (r4/(4a))].
E = (1/ε0)ρ0[(r/3) -(r2/(4a))].
Φ =
Φ(a) + ∫raE(r)dr = Φ(a) + (ρ0/ε0)∫ra[(r/3)
- (r2/(4a))]dr
= Φ(a) + (ρ0/ε0)[(r2/6)
- (r3/(12a))]ra
= (ρ0/ε0)[a2/12
+ a2/6 - a2/12 - r2/6 + r3/(12a)]
= (ρ0/ε0)[a2/6 - r2/6 + r3/(12a)].
(d) U = (ε0/2)∫all_space
E·E
dV
U
= (ρ02/2ε0)∫0a[(r2/9)
- (r3/(6a)) + (r4/(16a2))]4πr2dr
+ (ρ02a6/288ε0)∫a∞(1/r4)4πr2dr
= (ρ02a5/ε0)*0.0648.
or
U
= (1/2)∫0aρ(r)Φ(r)dV = (4π/2)∫raρ(r)Φ(r)r2dr
= (2πρ02/ε0)∫0a(1 -
r/a)[a2/6 - r2/6 + r3/(12a)]r2dr
= (ρ02a5/ε0)*0.0648.
Similar problem
Gauss' law, cylindrical symmetry
Problem:
A 500 m length of high-voltage cable is undergoing electrical testing. The
cable consists of two coaxial conductors, the inner of 5 mm diameter and the
outer of 9 mm internal diameter. The space between the conductors is filled
with polythene which has a relative permittivity of 2 and which can withstand
electric field strength of 60 MVm-1.
(a) Find the maximum voltage which can be applied between the conductors and
the energy stored in the cable at this voltage.
(b) If the cable is to be discharged to a safe level of 50 V in 1 minute, what
value of resistance must be connected across it? What is the maximum power and
the total energy dissipated in the resistance?
Solution:
- Concepts:
Gauss' law, the cylindrical capacitor
- Reasoning:
The problem has enough symmetry to find
D(r) and E(r) from Gauss'
law alone.
- Details of the calculation:
(a) From Gauss' law: D(r), E(r ) ∝ 1/r between the cylinders.
Let the outer cylinder be grounded and V0 be positive. Then the
direction of E is radially outward.
E(r) = A/r, with A positive. Then V0 = -∫b/2a/2E(r)dr
= A∫a/2b/2(1/r)dr
= A(lnb/2 - lna/2) = Aln(b/a). A = V0/ln(b/a),
with a = 5 mm and b = 9 mm.
E(r) = V0/(rln(b/a)).
If Emax = E(a/2) = 2V0/(aln(b/a)) = 60 MV/m, then
V0 = (6*107 V/m)*(2.5*10-3 m)*ln(9/5) = 8.82*104
V is the maximum voltage which can be applied.
Energy stored in the cable:
W = (ε/2)∫E2dV = (εL/2)2π∫a/2b/2E2rdr
= επL∫a/2b/2(V0/(rln(b/a)))2rdr.
W = [επLV02/ln(b/a)] = [2πε0(500 m)*(8.82*104
V)2/ln(9/5)] = 368 J.
Problem:
A plasma is generated inside a long hollow cylinder of radius R. It
has the charge distribution
ρ(r) = ρ0/(1 + (r/a)2)2,
where r is the distance to the center, and ρ0 and a are constants.
(a) What is the electric field inside and outside the cylinder?
(b) Setting V(r=0) = 0, find the potential at all points r < R.
(c) What are the equilibrium positions of a particle with charge q placed
inside the cylinder, assuming the charge does not alter ρ(r). What is the force
acting on the particle if it is displaced by a distance ε << a from an
equilibrium position. Are the equilibrium positions stable?
Solution:
- Concepts:
Gauss' law
- Reasoning:
Choose cylindrical coordinates. Then E will only have a radial component,
E
= E(r) (r/r).
- Details of the calculation:
(a)
For a volume of unit length: 2πrE = Qinside/ε0.
For r < R: 2πrE = (ρ0/ε0)2π∫0rr'dr'(1
+ (r'/a)2)-2.
ε0rE/ρ0 = ∫0rr'dr'(1 + (r'/a)2)-2
= a2∫0r/axdx(1 + x2)-2 =
(a2/2) ∫0Ydy(1 + y)-2 = -(a2/2)(1
+ y)-1|0Y
with Y = (r/a)2.
ε0rE/ρ0 = (a2/2)(1 - 1/(1 + (r/a)2))
= (r2/2) /(1 + (r/a)2).
For r < R: E(r) = ρ0r/(2ε0(1 + (r/a)2)),
E(R) = ρ0R/(2ε0(1 + (R/a)2)).
For r >R: 2πrE = (ρ0/ε0)2π∫0Rr'dr'(1
+ (r'/a)2)-2.
For r >R: E(r) = (ρ0R2/r)((2ε0(1 + (R/a)2)),
E = constant/r.(b) V(r < R) = -∫0rE(r')dr' = -(ρ0/(2ε0))∫0rr'dr'/(1
+ (r'/a)2) = -(ρ0a2/(2ε0))∫0r/axdx/(1
+ x2).
V(r < R) = -[ρ0a2/(4ε0)] ln((r/a)2
+ 1).
(c) All positions on the cylinder axis are equilibrium positions. With
respect to displacements along the cylinder axis these positions are neutral.
The force on the particle is zero.
With respect to small displacements ε from equilibrium perpendicular to the axis
of the cylinder the force is F = qE(r) ≈ qE(0) + q(dE/dr)|0ε
= q(dE/dr)|0ε = qρ0ε/(2ε0) (r/r).
This is a linear restoring force if q and ρ0 have opposite signs.
If q and ρ0 have opposite signs, then the equilibrium points are
stable.
If q and ρ0 have the same sign, then the equilibrium points are
unstable.
Gauss' law, planar symmetry
Problem:
Consider an infinite plane with a uniform charge
density σ located at z = 0.
(a) Using Gauss' law, find the electric field created by this plane.
(b) Find the potential Φ(z).
(c) Locate another plane with charge density -σ
at z = d. Find the potential Φ(z) everywhere.
What is the magnitude of the potential jump across the dipolar layer
configurations of the two planes?
(d) Find the force per unit area between the planes.
Solution:
- Concepts:
Gauss' law, the electric potential
- Reasoning:
We use Gauss' law to find the magnitude of the
field produced by the plane.
- Details of the calculation:
(a) The electric field is perpendicular to
the plane by symmetry.
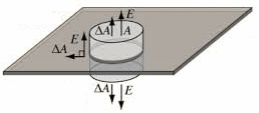
Flux through Gaussian
surface = 2E ΔA = σΔA/ε0
The field E produced by the
sheet is E = k σ/(2ε0) for z > 0 and E = -k
σ/(2ε0) for z < 0.
(b)
E = -k ∂Φ/ ∂z. Let Φ
= 0 at z = 0. Then Φ = -σ|z|/(2ε0) for
all z.
(c) The potential due to the second plate is Φ =
σ|z - d|/(2ε0) - σd/(2ε0).
Using the principle of
superposition we have Φtotal =
σ|z|/(2ε0) + σ|z - d|/(2ε0) + constant.
If we want to keep Φ = 0 at z = 0, then the constant equals
σd/(2ε0).
For z < 0: Φtotal = -σ|z|/(2ε0)
+ σ|z|/(2ε0) + σd/(2ε0) - σd/(2ε0) = 0
For 0 < z < d: Φtotal = -σz/(2ε0)
- σz|/(2ε0) + σd/(2ε0) - σd/(2ε0) = - σz/ε0.
For z > d: Φtotal = -σz/(2ε0)
+ σz|/(2ε0) - σd/(2ε0) - σd/(2ε0) = - σd/ε0.
The magnitude of the potential jump across the dipolar layer is
σd/ε0.
(d) For the two planes: E
= -k σ/ε0 between the planes,
E = 0 everywhere else.
The magnitude of the force per unit area between
the plates is F/A = σ<E> = σ2/(2ε0)
Alternative approach:
U = (ε0/2)E2 Ad = σ2/(2ε0) Ad, |F|
= |dU/d(d)| = σ2/(2ε0) A, F/A = σ2/(2ε0).
Problem:
A charge Q is placed a distance D from an infinite
slab of non-conducting material with charge density ρ
and thickness d. What is the force on the charge?
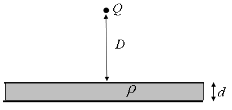
Solution:
- Concepts:
Gauss' law, F = QE
- Reasoning:
The problem has enough symmetry to find the electric field from Gauss' law
alone.
- Details of the calculation:
Outside the slab: Eoutside =
n ρd/(2ε0),
where n is a unit vector perpendicular to the closest surface and
pointing away from the surface. FQ =
n Qρd/(2ε0).




