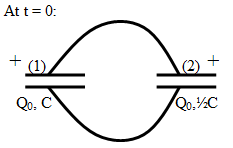Electrostatic energy, conductors and dipoles

Problem:

A charge Q is uniformly distributed through the volume of a sphere of radius R.  Calculate the electrostatic energy stored in the resulting electric field.

Problem:

(a)  A positive charge Q is spread over an semicircular arc with radius R as shown.
(1)  What is the work required to bring in a charge -q from infinity to the center of the arc?
(2)  Calculate the magnitude and direction of the force on a charge -q at the center of the arc.

(b)  The potential of a uniformly charged spherical shell of radius R centered at the origin is
V(r) = q/(4πε₀r) r ≥ R,   V(r) = q/(4πε₀R) r < R, 
where q denotes the total charge of the sphere.
Calculate the energy that it requires to deposit a charge Q on an initially neutral conducting spherical shell with radius R.  Use two different approaches to come to the result.
(3)  Calculate the energy by incrementally adding a charge dq to the sphere.
(4)  Obtain the energy by considering the resulting electric field of the spherical shell.

Solution:

• Concepts:
  Electrostatic potential energy and work
• Reasoning:
  The electric field is a conservative field, the work does not depend on the path.
• Details of the calculation:
  (1)  The potential (work per unit charge) due to the charge Q at the origin is 
  V = kQ/R,  k = 1/(4πε₀), SI units.
  W = -kqQ/R is the work required to bring in a charge -q from infinity to the center of the arc.
  (2)  The force will be F = Fj, pointing in the y-direction from symmetry.
  F = 2kq∫₀^π/2λRdθ sinθ/R² = (2kqλ/R)∫₀^π/2sinθ dθ = (2kqλ/R), with λ = Q/(πR).
  F = 2kqQ/(πR²).
  (3)  When a charge q has already been added to the sphere, the additional work needed to add another charge dq is kqdq/R.  The total work necessary to deposit a charge Q on the shell is
  W = (k/R)∫₀^Qqdq = ½kQ²/R.  This is the energy stored in the charge distribution.
  (4)  E = kQ/r² outside the shell, E = 0 inside the shell.
  The energy density in the electric field is u(r) = (ε₀/2)E(r)².  
  The total energy stored in the field is
  4π∫_R^∞r²dr u(r) = (4πε₀/2) ∫_R^∞r²dr k²Q²/r⁴ = [Q²/(8πε₀)] ∫_R^∞dr/r² = Q²/(8πε₀R) = ½kQ²/R.
  In electrostatics, viewing the energy as being stored in the charge distribution or viewing it as being stored in the electric field leads to the same results.

Problem:

(a) Show that the plates of an isolated parallel-plate capacitor attract each other with a force F = (Q²/2ε₀A), where ±Q are the charges on the plates and A is the area of each plate.
[HINT: Consider the work necessary to increase the plate separation from x to x + dx.]
(b) How does your answer to part (a) change if, instead, one maintains a constant potential difference between the plates of the capacitor?

Solution:

• Concepts:
  Work done by an external force F_ext:  W = F_ext∙Δr
  Energy stored in a capacitor:  U = ½(Q²/C) = ½CV².
  Capacitance of a parallel plate capacitor:  C = ε₀A/x, x = plate separation
• Reasoning:
  As we change the plate separation, the energy stored in the capacitor changes.
  ΔU = mechanical work done by external agent + work done by the battery.
• Details of the calculation:
  (a)  The battery is disconnected, the charge on the capacitor is constant.
  U = ½(Q²x/ε₀A),  ΔU = ½(Q²Δx/ε₀A) = F_extΔx.
  F_ext = dU/dx,  F = -F_ext = -dU/dx = -(Q²/2ε₀A) = -U/x, the force is attractive.
  (b)  The battery is connected, the voltage across the plates is constant.
  The force must be the same, however, the argument arriving at the expression is different.
  U = ½CV²,  ΔU = ½ΔCV².
  ΔU = F_extΔx + ΔQV,  dU/dx = F_ext + VdQ/dx
  dU/dx = ½V²dC/dx, Q = CV,  dQ/dx = VdC/dx.
  F_ext = -dU/dx,  F = -F_ext = dU/dx = ½V²dC/dx = -U/x

Problem:

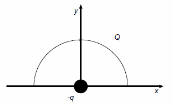
Assume you have two capacitors of capacitance C and ½C respectively, each holding a charge Q₀.  At t = 0 you connect then with wires as shown.

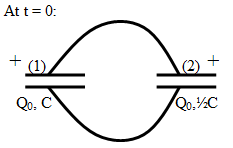
(a)  What is the energy stored in the capacitors at t = 0?
(b)  What is the energy stored in the capacitors at t --> infinity?
(c)  Explain the difference!

Solution:

• Concepts:
  Capacitors in parallel, energy stored in capacitors, energy conservation
• Reasoning:
  We are asked to find the change in the energy stored in two capacitors when they are connected in parallel.
• Details of the calculation:
  (a)  For a capacitor, U = ½Q²/C
  For (1):  U = ½Q₀²/C,  for (2) U = Q₀²/C, for both U = (3/2)Q₀²/C.
  (b)  C' = (3/2)C = capacitance of the capacitors in parallel.  Q' = 2Q₀.
  U' = ½ 4Q₀²/(3C/2) = (4/3)Q₀²/C.  U - U' = (1/6)Q₀²/C.
  (c)  Assume the wires have some resistance R.
  In the quasi-static approximation we have Q₁(t)/C - IR - 2Q₂(t)/C = 0.
  I = -dQ₁/dt, Q₁(t) + Q₂(t) = 2Q₀, therefore
  dQ₁/dt = -3Q₁/(RC) + 4Q₀/(RC).  Q₁ = (4/3)Q₀ - (1/3)Q₀exp(-3t/(RC)).
  As t --> infinity, Q₁ --> (4/3)Q₀,  V₁ --> (4/3)Q₀/C, independent of R.
  I(t) = -(1/(RC))Q₀exp(-3t/(RC)).
  Energy dissipated:  E = ∫₀^∞I²Rdt = Q₀²/(6C).
  This is exactly the difference in the energy stored in the capacitors at t = 0 and at t = infinity.  It is independent of R and does not change if we make R very small.

Problem:

Three identical capacitors (capacitance C) are connected in series to a source of electric potential V.   The capacitors are then individually disconnected from the source and wired in a new, series-parallel circuit in which two capacitors remain in series in their original orientation and the third is placed in parallel with the first two, with its positive plate connected to the positive end of the series pair, as shown in the figure.  Find the new potential difference, V', of the combined capacitors. 

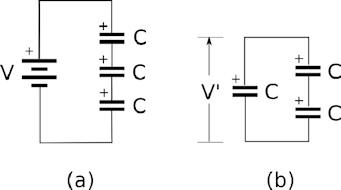
Solution:

• Concepts:
  Capacitance, capacitors in series and in parallel
• Reasoning:
  We have to consider different arrangements of three identical capacitors.
• Details of the calculation:
  In configuration (a) the charge on the upper plate of each capacitor is Q = CV/3.
  In configuration (b) the total capacitance is C' = C + C/2 = (3/2) C.
  The total separated charge is Q' = 2Q.
  V' = Q'/C' = 4V/9.

Problem:

A battery with voltage V charges a capacitor with capacitance C.  At t = 0 the battery is disconnected.  The positive plate of the capacitor is then connected to one plate of a previously uncharged identical capacitor by wire with zero resistance.  The negative plate of the charged capacitor is connected to the other plate of the second capacitor.
(a)  What is the energy stored in the capacitors at t = 0?
(b)  What is the energy stored in the capacitors at t --> infinity?
(c)  Explain the difference from the point of view of the energy conservation.

Solution:

• Concepts:
  Capacitors in parallel, energy stored in capacitors, energy conservation
• Reasoning:
  We have to consider different arrangements of two identical capacitors.
• Details of the calculation:
  (a)  For a capacitor, U = ½Q²/C = ½ CV².
  U = ½Q²/C,  Q = CV.
  (b)  C' = 2C = capacitance of the capacitors in parallel.  Q' = Q.
  U' = ½Q²/C' = ¼Q²/C,   U - U' = ¼Q²/C = ½U.
  (c)  The electric force does work on the charges when they move.  Since as t --> infinity the charges are again at rest and have no kinetic energy, the work done by the electric force is dissipated in the form of thermal energy or radiation.
  
  In the quasi-static approximation we have Q₁(t)/C - IR - Q₂(t)/C = 0.
  I = -dQ₁/dt, Q₁(t) + Q₂(t) = Q₀ therefore
  dQ₁/dt = -2Q₁/(RC) + Q/(RC).  Q₁ = Q + (Q/2) exp(-2t/(RC)).
  As t --> infinity, Q₁ --> Q/2,  V₁ --> V/2, independent of R.
  I(t) = -(1/(RC))Q exp(-2t/(RC)).
  Energy dissipated:  E = ∫₀^∞I²Rdt = Q²/(4C).
  This is exactly the difference in the energy stored in the capacitors at t = 0 and at t = infinity.  It is independent of R and does not change if we make R very small.

Problem:

Two isolated spherical conductors of radii 3 cm and 9 cm are charged to 1500 V and 3000 V, respectively.  They are very far away from each other.
(a) What is the total energy of the system?
(b) If we connect the two conductors by a fine wire and wait until equilibrium is established, how much heat will be generated in the wire?

Solution:

• Concepts:
  The energy stored in a capacitor
• Reasoning:
  Initially we have two isolate spherical capacitors.  We then connect them in parallel.
• Details of the calculation:
  (a)  We have two isolated spherical capacitors.  The total energy stored in the system is
  U = ½ (C₁V₁² + C₂V₂²).  For a spherical capacitor C = 4πε₀R.  Therefore
  U = 2πε₀(R₁V₁² + R₂V₂²) = 4.875*10^-5 J.
  The total charge on the capacitors is Q = Q₁ + Q₂ = C₁V₁ + C₂V₂ = 4πε₀(R₁V₁ + R₂V₂).
  (b) We have two capacitors in parallel with total charge Q and capacitance C = C₁ + C₂.
  The total energy stored in the system now is U' = ½Q²/C.
  U' = ½(4πε₀(R₁V₁ + R₂V₂))²/(4πε₀(R₁ + R₂)) = 2πε₀(R₁V₁ + R₂V₂)²/(R₁ + R₂)
  The energy dissipated as heat will be U - U' = 2πε₀(V₁-V₂)²R₁R₂/(R₁ + R₂)
  = 2.8125*10^-6 J.

Problem:

Two identical metal plates of area A each are arranged as shown: the top plate is suspended by a spring with a force constant k and the bottom plate is mounted underneath so that it does not move.  When both plates are neutral, the equilibrium distance between them is h.  If the plates are connected to a power supply, what maximum voltage between the plates would not cause them to touch and maintain a stable equilibrium?

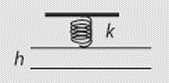
Solution

• Concepts:
  Stable equilibrium
• Reasoning:
  The electric force and the restoring force from the spring point in opposite directions.  When they have equal magnitude we have an equilibrium position.  We have to find the condition for the equilibrium to be stable.
• Details of the calculation:
  When the plate separation d << A^½, the plates can be treated like a parallel plate capacitor with capacitance C = ε₀A/d. 
  The field energy stored in the capacitor is U = ½CV².
  If we change the plate separation, the field energy stored in the capacitor changes.
  ΔU = mechanical work done by external agent + work done by the battery.
  Let the x axis point upward and let x = denote the plate separation.   If the position of the upper plate changes from x to x + Δx, then
  ΔU = F_extΔx + ΔQV.  F_ext = dU/dx - VdQ/dx = ½V²dC/dx - V²dC/dx
  = -½V²dC/dx, since Q = CV.
  F_ext = ½ε₀AV²/x².  F_electric = -F_ext = -½ε₀AV²/x². 
  The electric force is attractive and pulls the upper plate down.  In equilibrium the electric force is balanced by the elastic force pulling the upper plate upward.  The equilibrium position x' is given by  
  k(h - x') = ½ε₀AV²/x'², or V² = (2k/(ε₀A))(hx'² - x'³).
  For a stable equilibrium we need a restoring force for small displacements δ from equilibrium. 
  F_total(x' + δ) = k(h - x' - δ) - ½ε₀AV²/(x' + δ)².
  We need dF_total/dδ|_δ=0  < 0. 
  dF_total/dδ|_δ=0 = -k + ε₀AV²/(x' + δ)³|_δ=0 = -k +  (2k)(hx'² - x'³) /x'³ = -3k + 2kh/x'.
  We find V_max by setting dF_total/dδ|_δ=0  = 0.
  -3k + 2kh/x' = 0, x' = 2h/3.  V_max = [(8kh³/(27ε₀A)]^½.

Problem:

Prove that the interaction energy of two dipoles P₁ and P₂ separated by a relative position R is given by
(1/(4πε₀)[P₁∙P₂/R³ - 3(P₁∙R)(P₂∙R)/R⁵].

Solution:

• Concepts:
  The dipole field, a dipole in an external field
• Reasoning:
  We have one dipole in the external field of another dipole.  The energy of a dipole in an external field is U = -P∙E.
• Details of the calculation:
  Consider dipole P₂ in the external field of dipole P₁.  Choose your coordinate system such that P₁ is at the origin and P₂ is at R.
  Field of P₁ at R:  E(R) = (1/(4πε₀))[3(P₁∙R)R/R⁵ - P₁/R³].
  Energy of  in this field: U = -P₂∙E(R) = (1/(4πε₀))[P₁∙P₂/R³ - 3(P₁∙R)(P₂∙R)/R⁵].