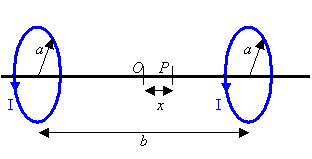The Biot-Savart law

Problem:

(a)  A circular loop of wire of radius R carries a current I.  Find the magnetic induction B on the axis of the loop, as a function of the distance z from the center of the loop.
(b)  Use the result to find B at points on the axis of a solenoid of radius R and length L wound with n turns per unit length.
(c)  Use this result to find the self-inductance of a very long solenoid (L >> R).

Solution:

• Concepts:
  The Biot-Savart law, the principle of superposition, self inductance
• Reasoning:
  We find the field of a single loop using the Biot-Savart law.  The principle of superposition then yields the field of many loops.
• Details of the calculation:
  
  (a)  From the Biot-Savart law we have
  dB_z(r) = (μ₀/(4π))[I dl' x (r-r')/|r-r'|³] ∙ k.
  On the z-axis r  = zk.
  Symmetry dictates that B = B_zk on the z-axis.
  dl = Rdφ (φ/φ), r - r' = z k - R (ρ/ρ),
  dl × (r - r') = zRdφ (ρ/ρ) - R²dφ  k.
  dB_z = (μ₀/(4π))[IR²dφ/(R²+z²)^3/2].
  B_z = ∫₀^2πdB_z = ½μ₀IR²/(R² + z²)^3/2.
  
  At the center of the loop B_z = μ₀I/(2R), and for z >> R we have B_z = μ₀IR²/(2z³).
  For z >> R the field is proportional to 1/z³.
  (b) Assume N loops are stacked up, from z' = -z₁ to z' = z₁, n per unit length.
  B_z = ½μ₀IR²∫_-z1^z1ndz'/(R² + (z-z')²)^3/2 = ½μ₀IR²n∫_z-z1^z+z1dz''/(R² + z''²)^3/2.
  B_z = ½μ₀IR²n{(z + z₁)/[R²(R² + (z+z₁)²)^½] - (z - z₁)/[R²(R² + (z-z₁)²)^½]}.
  
  cosθ₁ = (z + z₁)/(R² + (z + z₁)²)^½,  cosθ₂ = (z - z₁)/(R² + (z - z₁)²)^½.
  B_z = (μ₀In/2)(cosθ₁ - cosθ₂)
  For the solenoid n = N/L, z₁ = L/2.
  (c)  At the center of the solenoid
  B = B_zk.  B_z = (μ₀In/2)(2z₁/(R² + z₁²)^½) = (μ₀IN/2)((R² + (L/2)²)^-½).
  If L >> R then B_z ≈ (μ₀In).
  The field is approximately uniform inside the solenoid and approximately zero outside the solenoid.
  F = L₁I, F = Flux, L₁ = self inductance.
  F = BπR²N = μ₀InπR²N = L₁I, L₁ = μ₀n²πR²L = μ₀n²V,  V = volume of the solenoid.

Problem:

A circuit in the form of a regular polygon of n sides is circumscribed about a circle of radius a.  
(a)  If it is carrying a current I, find the magnitude of the magnetic field B at the center of the circle in terms of μ₀, n, I, and a.  
(b)  Find B at the center of the circle as n is indefinitely increased.  

Solution:

• Concepts:
  The Biot-Savart law, the principle of superposition
• Reasoning:
  We find the field of a single segment using the Biot-Savart law. 
  The principle of superposition then lets us add the fields of the  different segments.
• Details of the calculation:
  (a)  The field B at the center of the circle due to the current in the wire from -l to +l is 
  B(r) = (μ₀/(4π))∫_vI dl' × (r-r')/|r-r'|³.   (SI units).
  
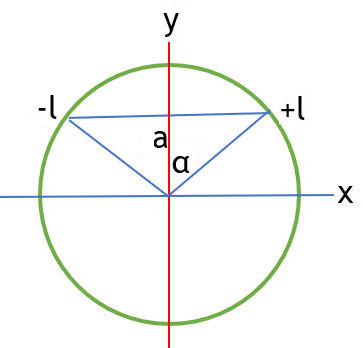
  Here r = 0,  r' = xi + aj,  dl' = dxi,  |r-r'| = (x² + a²)^½. 
  dl' × (r-r') = -(a dx) k.
  B = -[μ₀I/(4πa)]2l/(l² + a²)^½ k = -[μ₀I/(2πa)]sin(α) k.
  For a regular plane polygon of n sides we have n wire segments.
  Example:  hexagon
  
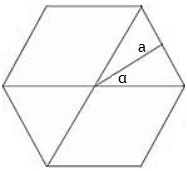
  For each segment 2α = 2π/n,  α = π/n.
  Symmetry dictates that B(0) due to each segment is the same. 
  B(0) = -[nμ₀I/(2πa)]sin(π/n) k.  B(0) = -[nμ₀I/(2πa)]sin(π/n).
  b)  As n --> ∞, sin(π/n) --> π/n,  B(0) --> nμ₀I/(2πa)](π/n) = μ₀I/(2a).
  This is the magnetic field at the center of a circular current loop of radius a.

Similar problems

Problem:

Find the magnetic field at the center of a circular loop of radius R that is formed in a long straight thin wire that carries current I; use the SI system of units.

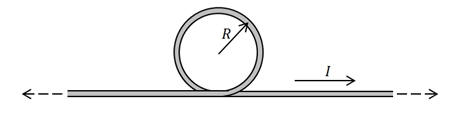
Solution:

• Concepts:
  The magnetic field of a long straight wire and a current loop.
• Reasoning:
  We use the principle of superposition.
• Details of the calculation:
  B(r) = [μ₀I/(2πR)][π + 1]  out of the page

Problem:

In practical magnetic structures, uniform magnetic fields are frequently necessary.  The uniformity of the field produced by Helmholtz coils, or two co-axial loops which carry currents in the same direction, is one of their most important characteristics.  Assume that the coils have a radius a, have axes on the x-axis, carry current I each, and are separated by a distance b.

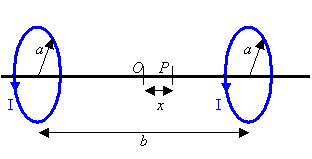
(a)  Find the magnetic field at a point P on the axis of the loops and a distance x from the midpoint O.
(b)  Expand the expression for the field in a power series, retaining terms to order x².
(c)  What relationship must exist between a and b such that the x² terms vanish?  What is the significance of this?
(d)  Show that the field created by the coils to this order and under the conditions established in part c is given by B_x = 8I/(5^3/2aε₀c²).

Solution:

• Concepts:
  The Biot-Savart law, a series expansion
• Reasoning:
  The magnetic field on the axis of a current loop is found from the Biot-Savart law.  Expanding the field near x = 0 in terms of x, we can find the condition for the second order term to vanish.  The first order term is be zero due to the symmetry of the situation, so B(x) = B(0) to second order if the term proportional to x² vanished.
• Details of the calculation:
  (a)  B = B(x)i on the x-axis. 
  B(x) = (μ₀Ia²/2)[a² + (d-x)²]^-3/2 + (μ₀Ia²/2)[a² + (d+x)²]^-3/2. 
  Here d = b/2.
  (b)  B(x) = B(0) + x(∂B/∂x)|₀ + (x²/2)(∂²B/∂x²)|₀ + ...
  ∂B/∂x =(μ₀Ia²/2)[-(3/2)2(d+x)[a² + (d+x)²]^-5/2 + (3/2)2(d-x)[a² + (d-x)²]^-5/2,
  (∂B/∂x)|₀ = 0.
  ∂²B/∂x² = (3μ₀Ia²/2)[5(d+x)²[a² + (d+x)²]^-7/2 - [a² + (d+x)²]^-5/2
  + 5(d-x)²[a² + (d-x)²]^-7/2 - [a² +( d-x)²]^-5/2].
  (∂²B/∂x²)|₀ = (3μ₀Ia²/2)[10d²[a² + d²]^-7/2 - 2[a² + d²]^-5/2]
  = (3μ₀Ia²/2)[(8d²-2a²)[a² + d²]^-7/2].
  (c)  For the second order term to vanish we need 8d²-2a² = 0, d = a/2,  b = a.  The field is then uniform to second order.
  (d)  B(x) = B(0) = (μ₀Ia²)[a² + d²]^-3/2
  = (μ₀I/a)[1 + ¼]^-3/2 = (μ₀I/a)(4/5)^3/2 = 8I/(5^3/2aε₀c²).

Problem:

An AC voltage source V(t) = V₀sinωt is connected to a wire of resistance R which forms a circular loop of radius a.  The wire loop rotates about the z-axis with angular frequency ω.  Find the instantaneous and the average magnetic field B (magnitude and direction) at the center of the loop.  Neglect the self-inductance of the loop.

Solution:

• Concepts:
  The magnetic field at the center of a current loop
• Reasoning:
  The magnetic field at the center of the loop has time varying x and y components.
• Details of the calculation:
  I(t) = V(t)/R = (V₀/R)sinωt = I₀sinωt.
  B(t) = μ₀I(t)/(2a) = μ₀I₀sinωt/(2a) = B₀sinωt.  B₀ = μ₀V₀/(2a).
  B(t) is the magnetic field at the center of the loop along the n direction.
  B(t) = B₀sinωt(cos(ωt)i + sin(ωt) j)  is the instantaneous magnetic field at the center of the loop expressed in terms of its components along the axes of the coordinate system.
  The average values of its components are
  <B_x> = B₀<sin(ωt) cos(ωt)> = 0,
  <B_y> = B₀<sin²(ωt)> = B₀/2.
  The average magnetic field is B = (B₀/2) j.