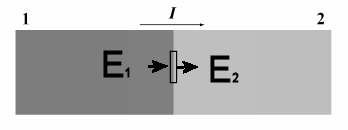Ohm's law, power

Problem:

A linear accelerator produces a beam of electrons in which the current is not constant but consists of a pulsed beam of particles.  Suppose that the pulse current is 1.6 A for a 0.1 μs duration. 
(a)  How many electrons are accelerated in each pulse?
(b)  What is the average beam current if there are 1000 pulses per second?
(c)  If the electrons are accelerated to an energy of 400 MeV, what is the average beam power on target?
(d)  What is the peak beam power on target?
(e)  What fraction of the time is the accelerator actually delivering beam on target?  (This is called the duty factor of the accelerator.)

Solution:

• Concepts:
  Basic concepts:  Charge, current, energy, power.
• Details of the calculation:
  (a)  Q = 1.6*10^-7 C/pulse,  N = Q/(1.6*10^-19 C) = 10¹² electrons/pulse.
  (b)  Average beam current = I_avg = 1.6*10^-7 C * 1000/s = 1.6*10^-4 A.
  (c)  Average power on target
   = 10¹² * 400 MeV * 1.6*10^-13 J/MeV / 10^-3 s = 64 kW.
  (d)  Peak power on target =10¹² * 400 MeV * 1.6*10^-13 J/MeV / 10^-7 s = 640 MW.
  (e)  Duty factor = 10^-7/10^-3 = 10^-4.

Ohm's law, resistance, power

Problem:

Two metallic spheres of the same radius r are immersed in a homogeneous liquid with resistivity ρ.  What is the total resistance between two spheres?  Assume that the distance between two spheres is much larger than the sphere radius.

Problem:

A current I flows through a wire made of a piece of material 1 and a piece of material 2 of identical cross-sections A welded end-to-end as shown in the figure.  The resistivity of material 1 is ρ₁, the resistivity of material 2 is ρ₂.  How much electric charge accumulates at the boundary between the two materials?

Solution:

• Concepts:
  Ohm's law, j = σ_cE = E/ρ, Gauss' law
• Reasoning:
  The same current is flowing in each section of the wire.
• Details of the calculation:
  I = jA, j₁ = j₂,  E₁/ρ₁ = E₂/ρ₂. 
  Apply Gauss' law to the interface.
  
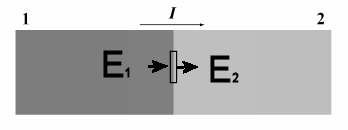
  E₂ - E₁ = σ/ε₀,  Q = ε₀A(ρ₂ - ρ₁)j ,  Q = ε₀I(ρ₂ - ρ₁).

Problem:

A copper wire (ρ = 1.72*10^-8 Ωm) has a length of 160 m and a diameter of 1.00 mm.  If the wire is connected to a 1.5 V battery, how much current flows through the wire?

Solution:

• Concepts:
  Ohm's law, resistance of a wire
• Reasoning:
  The current can be found from Ohm's Law, V = IR.  V is the battery voltage, so if R can be determined, the current can be calculated.  The resistance of the wire is R = ρl/A.
• Details of the calculation:
  For copper ρ = 1.72*10^-8 Ωm.
  The cross-sectional area of the wire is A = πr² = π(0.0005)² = 7.85*10^-7 m².
  The resistance of the wire then is ((1.72*10^-8)*160/(7.85*10^-7)) Ω = 3.5 Ω.
  The current is I = V/R = (1.5/3.5) A = 0.428 A.

Problem:

One can locate resistivity anomalies in the ground as shown in the figure below.

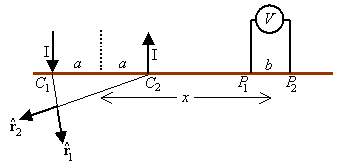
The current I flowing between electrodes C₁ and C₂ establishes an electric field in the ground.  One measures the voltage V between a pair of electrodes, with P₁ and P₂ maintained at a fixed spacing b. With b << a, V/b is equal to E at the position x.  Anomalies in ground conductivity show up in the curve of as a function of x.
Show that if the substrate conductivity is uniform and equal to σ, then
V/b = 2axI/[πσ(x² - a²)²].
The electrodes are of finite size.  However, you can perform the calculation on the assumption that they are infinitely small, disregarding the fact that E and j would then be infinite at their surfaces.
You can use the principle of superposition as follows.  The current in the ground is the sum of a radial distribution emanating from C₁ plus another radial distribution converging on C₂.

Solution:

• Concepts:
  Conductivity, E = j/σ_c
• Reasoning:
  The field in the ground is a superposition of a field E₁ which points radially away from point C₁ and a field E₂ which points radially towards point C₂.  Therefore the current in the ground is the sum of a radial distribution emanating from point C₁ and another radial distribution converging on C₂.  At some point a distance r₁ from C₁ and a distance r₂ from C₂ we have
  E = j₁/σ_c + j₂/σ_c = (r₁/r₁)I/(2πσ_cr₁²) - (r₂/r₂)I/(2πσ_cr₂²).
• Details of the calculation:
  On the axis at position x we have E = [I/(2πσ_c)][1/(x + a)² - 1/(x - a)²] i.
  E = [I/(2πσ_c)](-4xa)/(x² - a²)² i = -2axI/[πσ(x² - a²)²] i.
  E = V/b = 2axI/[πσ(x² - a²)²].

Problem:

A high-voltage transmission line that connects a city to a power plant consists of a pair of copper cables, each with a resistance of 4 W.  The current flows to the city along one cable, and back along the other.
(a)  The transmission line delivers to the city 1.7*10⁵ kW of power at 2.3*10⁵ V.  What is the current in the transmission line?  How much power is lost as Joule heat in the transmission line?
(b)  If the transmission line delivers the same 1.7*10⁵ kW of power at 110 V, how much power would be lost in Joule heat?  Is it more efficient to transmit power at high voltage or at low voltage?

Solution:

• Concepts:
  Circuits, voltage, current, resistance, power
• Reasoning:
  Power delivered: P_delivered = IV,  P_lost = I²R.
• Details of the calculation:
  (a)  The power delivered to the city, P_delivered, is equal to 1.7*10⁵ kW.  The voltage V is equal to 2.3*10⁵ V.  The current through the cables therefore is I = P/V = 7.4*10² A.  This current is flowing through the transmission cables.  The electric energy dissipated in the cables is equal to
  P_lost = I²R = (7.4*10²)²*8 W = 4.4*10⁶ W.
  The power generated by the power plant therefore is
  P = P_delivered + P_lost = 1.74*10⁵ kW.
  98% of the generated power is delivered to the city.
  (b)  The power delivered to the city, P_delivered, is equal to 1.7*10⁵ kW.  The voltage V is equal to 110 V.  The current through the cables therefore is I = P/V = 1.6*10⁶ A.  This current is flowing through the transmission cables.  The electric energy dissipated in the cables is equal to
  P_lost = I²R = (1.6*10⁶)²*8 W = 1.9*10¹³ W.
  The power generated by the power plant therefore is
  P = P_delivered + P_lost = 1.9*10¹³ kW.
  Only 0.0009% of the generated power is delivered to the city.  Transmission of electrical energy at high voltage is much more efficient that the transmission at low voltage.  The voltage of the transmission line is therefore reduced to 110 V as close as possible to the house of the customer.