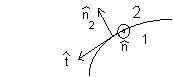Maxwell's equations for magnetostatics, boundary conditions

Problem:

Find the magnetic vector potential for the case of a long, straight wire carrying a steady current I.  Let R be the radius of the wire.

Problem:

A converging magnetic field is often used as a magnetic mirror.  Consider a symmetric converging field with ∂B_z/∂z = f(z).   Show that the radial component of B in cylindrical coordinates, namely B_ρ, where ρ = xi + yj is given by B_ρ = -(ρ/2)f(z).

Solution:

• Concepts:
  Gauss's law for B
• Reasoning:
  ∇∙B = 0, ∂B_z/∂z = f(z) is given, the field has no φ dependence, we can solve for B_ρ.
• Details of the calculation:
  ∇∙B = 0, ∂B_x/∂x + ∂B_y/∂y = -∂B_z/∂z = -f(z).
  In cylindrical coordinates: (1/ρ)∂(ρB_ρ)/∂ρ + (1/ρ) ∂B_φ/∂φ = -f(z).
  For the symmetric converging field B_φ = 0, so ∂(ρB_ρ)/∂ρ = - ρf(z),
  ρB_ρ = - ρ²f(z)/2, B_ρ = - ρf(z)/2.

Problem:

At the interface between one linear magnetic material and another the magnetic field lines bend.  Show that tanθ₂/tanθ₁ = μ₂/μ₁, assuming there are no free currents at the boundary.

Solution:

• Concepts:
  Boundary conditions for B and H
• Reasoning:
  No free currents are at the interface.  The normal component of B and the tangential component of H therefore have to be continuous at the boundary.
• Details of the calculation:
  (a) Assume B₁ makes an angle θ₁ with the normal to the interface in the medium with m₁.
  B_1x/B_1y = tanθ₁.
  

  B_y is continuous across the boundary.  H_x is continuous across the boundary.  In the medium with μ₁ we have H_1x = B_1x/μ₁.  In the medium with μ₂ we have H_2x = B_2x/μ₂.  H_1x = H_2x.  B_1xμ₂/μ₁ = B_2x.
  B_2x/B_2y = (B_1xμ₂)/(B_1y μ₁) = tanθ₂ = (μ₂/μ₁ )tanθ₁.
  Comment: This will remind you of refraction, but different boundary conditions for the normal and tangential components of E, D and B, H result in a different formula.

Problem:

(a)  Find the magnetic field B of a rotating spherical shell with uniform surface charge density σ.
(b)  Find the magnetic field  B of a uniformly magnetized sphere.

Solution:

• Concepts:
  Boundary conditions, the uniqueness theorem, Magnetization M, magnetization current densities
• Reasoning:
  We can solve for the magnetic field of a rotating spherical shell with uniform surface charge density σ, by treating the problem as a boundary value problem.  The magnetization of a uniformly magnetized sphere results in a magnetization surface current density like the surface current density of a rotating spherical shell with uniform surface charge density σ.
• Details of the calculation:
  (a)  Let the radius of the sphere be R, its center be located at the origin, and let the sphere rotate with angular velocity ω = ωk.
  The rotating surface charge density produces a surface current density, k_m = σω x R, 
  k_m = σωRsinθ.
  For r >> R we will have a dipole potential,
  A(r) = (μ₀/(4π))m x r/r³, or A_φ = (μ₀/4π)msinθ/r².
  To find the dipole moment m, we consider the rotating sphere to be a stack of current loops.
  For a current loop at θ we have dm = IA = Rσω sinθ Rdθ πR²sin²θ = R⁴σωπ sin³θdθ.
  Integrating dm from θ = 0 to θ = π we find m = (4/3)R⁴σωπ, m = mk.
  [∫sin³xdx = -(1/3)cosx (sin²x + 2)]
  For r >> R we have A_φ = (μ₀/3)R⁴σωsinθ/r².
  ∇²A(r) = -μ₀j(r),  A(r) = (μ₀/(4π)) ∫_V'dV' j(r')/|r - r'|.  (SI units).
  Assume that A(r) will only has φ component.
  Assume that the 1/r² term is the only term in the expansion of A in powers of 1/rⁿ outside of the sphere, i.e. assume that outside the sphere the potential is a pure dipole potential.
  Since A must be continuous at r = R and A must be finite at the origin,
  assume that A_φ = Csinθr = (μ₀/3)Rσωsinθr  inside the sphere.
  
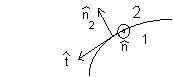
  If this solution fulfills the boundary conditions,
  (B₂ - B₁)·n₂ = 0,  (B₂ - B₁)·t = μ₀k·n,
  we have the only solution.
  B = ∇×A,  
  B_{in_r} =  (1/)rsinθ))∂(sinθA_{φ_in})/∂θ = (2μ₀/3)Rσω cosθ, = (μ₀/4π)2m cosθ/R³.
  B_{in_θ} =  -(1/r)∂(rA_{φ_in})/∂r = -(2μ₀/3)Rσω sinθ = -(μ₀/4π)2m sinθ/R³.
  B_{out_r} =  (1/(rsinθ))∂(sinθA_{φ_out})/∂θ = (2μ₀/3)R⁴σω cosθ/r³  = (μ₀/4π)2m cosθ/r³.
  B_{out_θ} =  -(1/r)∂(rA_{φ_out})/∂r = (μ₀/3)R⁴σωsinθ/r³ = (μ₀/4π)m sinθ/r³.
  Now check that the boundary conditions are satisfied.
  At r = R the radial component of B is continuous.
  B_{out_θ} - B_{in_θ} = μ₀R⁴σω sinθ/R³ = μ₀k_m.
  The boundary conditions are satisfied and we have the only solution.
  The field outside the sphere is a pure dipole field,
  B(r) =  (μ₀/(4π))[3(m∙r₁)r₁/r₁⁵ - m/r₁³],
  and the field inside the sphere is constant,  B(r) = k(μ₀/4π)2m/R³.
  (b)  For a uniformly magnetized sphere with radius R and M = Mk we have m = (4/3)πR³M. 
  The magnetization current densities are j_m = 0, k_m = M × R/R, k_m = Msinθ .
  We may write k_m = (3m/(4πR³)sinθ.
  Expressed in terms of the magnetic moment m the uniformly magnetized sphere has the same surface current density as the rotating spherical shell with uniform surface charge density σ.
  The same currents produce the same fields.
  The field outside the uniformly magnetized sphere is a pure dipole field,
  B(r) =  (μ₀/(4π))[3(m∙r₁)r₁/r₁⁵ - m/r₁³],
  and the field inside the sphere is constant,  
  B(r) = k (μ₀/4π)2m/R³ = (μ₀/4π)(8π/3)M.
  
  Comment:

  It is important that you remember the following from this problem:
  The magnetic field of a uniform magnetized sphere outside the sphere is a pure dipole field 
  B(r) =  (μ₀/(4π))[3(m∙r₁)r₁/r₁⁵ - m/r₁³,
  The dipole moment is m = MV = M4πR³/3.
  The magnetic field inside the sphere is constant (magnitude and direction).
  
  If you place the origin of the coordinate system at the center of the sphere and let M = Mk, then you can find the magnitude of the field inside by matching it to the field outside on the z-axis at z = R.
  A uniform magnetized sphere has a magnetization surface current distribution
  k_m = M × R/R, k_m = Msinθ .
  Any surface distribution of the same form produces the same fields.