Transients, RL circuits

Problem:

A 3 m long solenoid with a diameter of 0.05 m has 3000 turns of wire with total resistance of 1 Ω uniformly wound along its length.  It has an air core. 
(a)  Find the approximate self-inductance of this solenoid.
(b)  If the solenoid and a 9 Ω resistor are connected in parallel across the terminals of a 12 V battery, find the final steady state current in the solenoid.
(c)  If the battery is disconnected at time 0 leaving the circuit of the solenoid and the resistor intact, find the current in the resistor as a function of time.
(d)  Show that the I²R losses in the resistor after t = 0 is equal to the energy stored in the solenoid at t = 0.

Solution:

• Concepts:
  Self inductance, Kirchhoff's rules, RL circuits
• Reasoning:
  The coil, resistor and battery form an RL circuit, which can be analyzed using Kirchhoff's rules.
• Details of the calculation:
  (a)  B = μ₀nI = magnitude of B inside the solenoid.
  F = NBπR² = LI = flux.  L = Nμ₀nπR² = μ₀n²πR²l,  l = length of solenoid,  n = N/l.
  L = (4π*10^-7 N/A²)*(1000 m^-1)²*π(0.025 m)²*3m = 7.4*10^-3 H.
  (b)  I_s = 12 V/1 Ω = 12 A.
  
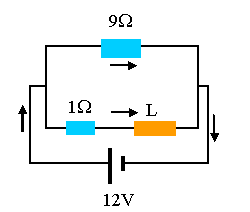
  (c)  LdI/dt + RI = 0.  R = 10 Ω.
  I = I₀ exp(-Rt/L) = 12 A exp(-10 Ωt/(7.4*10^-3 H)) = 12 A exp(-1351 t/s)
  The current through the solenoid is decaying exponentially.
  (d)  P = I²R = 144 A² exp(-2703 t/s)*10 Ω.
  Energy dissipated = ∫₀^∞ P dt = 0.53 J.
  Energy stored in solenoid at t = 0:  E = ½LI² = ½(7.4*10^-3 H)(12 A)² = 0.53 J.

Problem:

A solenoid of length l = 1 m and cross-sectional area A = 1 cm² has N = 10000 turns of wire with a total resistance of 1 ohm.  At t = 0 the solenoid is connected to a V = 100 V power supply.  Find the total work done by the power supply in the time interval it takes for the current to increase from zero to (1 - 1/e) = 0.6321 times its steady state value.  Give a numerical answer.

Solution:

• Concepts:
  Induced emf, transient
• Reasoning:
  As the current changes, an emf = -LdI/dt is induced.  Here L is the self-inductance of the solenoid.
• Details of the calculation:
  Kirchhoff's loop rule yields
  V = LdI/dt + IR,   and   I(t) = (V/R)(1 - exp(-(R/L)t).
  The time it takes for the current to increase from zero to (1 - 1/e) times its steady state value is found from
  (1 - 1/e) = 1 - exp(-(R/L)t),  t = L/R. 
  The power supplied by the battery is
  P = VI = dW/dt.
  The total work done in the time interval from t = 0 to t = L/R is
  W = (V²/R) ∫₀^L/R(1 - exp(-(R/L)t)dt.
  ∫₀^L/R(1 - exp(-(R/L)t)dt = L/R - (L/R)(1 - 1/e).
  W = LV²/R² (1/e) = 0.3678 LV²/R².
  We can also write W = ½ LI²(t = L/R) + ∫₀^L/RI²(t) R dt =
  (L/2)(1 - 1/e)²(V²/R²) + (V²/R) ∫₀^L/R(1 - exp(-(R/L)t)²dt,
  since the battery has to supply the energy dissipated in the resistance and the energy stored in the magnetic field of the coil.
  ∫₀^L/R(1 - exp(-(R/L)t)²dt = ∫₀^L/R(1 - 2exp(-(R/L)t + exp(-(2R/L)t)dt
  = L/R - 2(L/R)(1 - 1/e) + (L/2R)(1 - 1/e²) = (L/R)(2/e - 1/(2e²) -½)
  = (L/R)*0.168
  W = 0.1998*LV²/R² + 0.168*LV²/R² = 0.3678 * LV²/R².
  The self-inductance of a solenoid is L = μ₀N²A/l .
  For the given solenoid we therefore have L = 1.26*10^-2 J/A², and V²/R² = 10⁴ A².
  We therefore have for the work W = 46.4 J.

Problem:

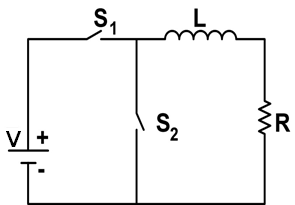
The circuit above is composed of a constant voltage source V, an inductor L, a resistor R and two switches S₁ and S₂.  Prior to time t = 0 both switches S₁ and S₂ are open.
(a)  What is the current flowing through the inductor L immediately after S₁ is closed at t = 0?
(b)  What is the steady-state current flowing through the inductor L at a much later time t₁?
(c)  At time t₂ > t₁ S₂ is closed and S₁ is opened at the same time.  Write a differential equation and solve it to find the current flowing through the inductor as a function of time .
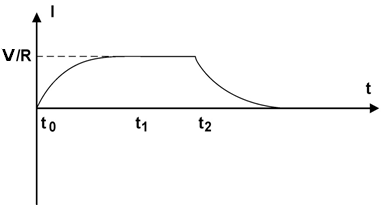
(d)  Sketch the current flowing through the in the inductor L, from time t = 0 until a time much later than t₂.

Solution:

• Concepts:
  RL transient circuits
• Reasoning:
  We are asked to analyze the transient behavior of an RL circuit.
• Details of the calculation:
  (a)  Immediately after S₁ is closed the current through the inductor L is zero.
  V - LdI/dt - RI = 0.  dI/dt = -(R/L)I +V/L,  I(t) = (V/R) (1 - exp(-Rt/L)).
  (b)  The steady state current through the inductor is I = V/R.
  (c)  LdI/dt + RI = 0
  dI/I = (-R/L)dt,  ∫ dI/I = -∫ (R/L)dt,  ln(I) = (-R/L)t + C
  At t = t₂, the current is V/R, so ln(V/R) = (-R/L)t₂ + C.
  ln(I) = (-R/L)t + ln(V/R) + (R/L)t₂
  ln(RI/V) = (-R/L)(t - t₂)
  RI/V = e^{(-R/L)(t - t}₂⁾
  I = (V/R)e^{-(t - t}₂^)R/L for any t > t₂
  (d)
  

Problem:

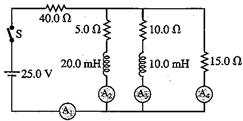
In the circuit shown in the figure, switch S is closed at time t = 0.
(a)  Find the current reading of each meter just after S is closed.
(b)  What does each meter read long after S is closed?

Solution:

• Concepts:
  Transient in RL circuits
• Reasoning:
  At t = 0, the inductor acts like an open circuit, a long time after the switch is closed the inductor acts like a short circuit. 
• Details of the calculation:
  (a)  A₂ an A₃ read zero, A₁ an A₄ read I = (25 V)/(55 Ω) = 0.45 A.
  (b)  R_eff = (40 + 30/11) Ω = (470/11) Ω.  I_total = V/R_eff = 55/94 A = 0.585 A.
  The voltage across the 5 Ω, 10 Ω, and 15 Ω  resistors in parallel is 1.6 V.
  I₂ = 0.319 A,  I₃ = 0.16 A,  I₄ = 0.106 A,
  A₁ reads 0.585 A,  A₂ reads 0.319 A,  A₃ reads 0.16 A,  A₄ reads 0.106 A.

Problem:

(a)  Suppose a capacitor is charged by a voltage source, and then switched to a resistor for discharging.  Would a larger capacitance value result in a slower discharge, or a faster discharge?  How about a larger resistance value? 

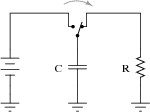
(b)  Now consider an inductor, "charged" by a current source and then switched to a resistor for discharging.  Would a larger inductance value result in a slower discharge, or a faster discharge?  How about a larger resistance value?