The Doppler effect

Problem:

A light beam of intensity I₀ and frequency f₀ propagating along the positive z-axis is reflected normally from a perfect mirror moving along the z-axis with speed v.  What is the intensity and the frequency of the reflected light?

Solution:

• Concepts:
  The Doppler effect, frame transformations.
• Reasoning:
  In the rest frame of the mirror, the incident and the reflected beam have the same frequency and intensity.  We use the Doppler formula and transform from the laboratory frame to the mirror frame and back to the laboratory frame.
  To find the ratio of the intensities of the incident and reflected beam in the laboratory frame we transform the electric field amplitude from the laboratory frame to the mirror frame and back to the laboratory frame.
• Details of the calculation:
  
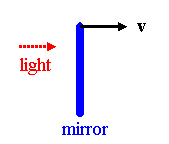
  In the rest frame of the mirror the incident beam has frequency f' = f₀[(c-v)/(c+v)]^½.
  The reflected beam has the same frequency.
  In the lab frame the reflected beam has frequency
  f = f'[(c-v)/(c+v)]^½ = f₀[(c-v)/(c+v)].
  The intensity of a light beam is proportional to E_⊥².  Denote the electric field amplitude of the incident beam in the laboratory by E_0⊥².
  
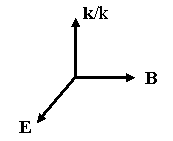
  In the rest frame of the mirror we have E'_⊥ = γ(E₀ + v×B)_⊥ = γE_0⊥(1 - v/c),
  since for a plane wave B = (1/c)(k/k)×E, where k/k is the direction of propagation of the wave.
  Here k/k denotes the z-direction and v is in the z-direction.
  The reflected beam in the lab frame has amplitude
  E''_⊥ = γ(E' - v×B')_⊥ = γE'_⊥(1 - v/c) = γ²E_0⊥(1 - v/c)² = E_0⊥(c-v)/(c+v).
  Note that for the reflected wave k/k denotes the -z-direction.
  The intensity is proportional to the square of the amplitude.
  I/I₀ = [(c-v)/(c+v)]².

Problem:

Consider two ultra-high-speed drag racers.  One drag racer has a red stripe on the side and overtakes the other drag racer at a relative speed of 3^½c/2 .  If the red stripe has wavelength 635 nanometers, what color is the stripe as observed by the other drag racer (that is, what is the wavelength) at the exact instant the overtaking occurs as measured in the frame of the racer-being-overtaken?

Solution:

• Concepts:
  The Doppler effect
• Reasoning:
  The frequency f of a sinusoidal electromagnetic wave with wave vector k (k = 2π/λ = ω/c) in a reference frame K is measured as f' in a reference frame K' moving with uniform velocity v with respect to K.
  f' = γf(1 - (v/c)cosθ), where θ is the angle between the directions of k and v.  Here θ = 90^o, f' = γf.
  (Note:  The slower racer will not observe the light at the exact instant the overtaking occurs as measured in his/her frame due to the finite speed of the light.)
• Details of the calculation:
  The frequency of the emitted light is f = c/λ = 4.72*10¹⁴/s, f '= γf and γ = 2. Thus f = 2*4.72*10¹⁴/s = 9.45*10¹⁴ Hz.  The wavelength is just halved to 318 nanometers.  This is in the violet to ultra-violet range.

Problem:

A train is moving directly towards you at 2*10⁸ m/s.  The (monochromatic) light on the front of the train has a wavelength of 250 nanometers in the frame of the train.  What wavelength do you observe?

Solution:

• Concepts:
  The Doppler effect
• Reasoning:
  The light is blue-shifted.  f' = f₀[(c +v )/(c -v )]^½.
• Details of the calculation:
  f₀ = c/λ = 1.2*10¹⁵ Hz.  f' = 1.2*10¹⁵ Hz[(1 + 0.667)/(1 - 0.667)]^½ = 2.68*10¹⁵.
  λ' = c/f' = 112 nm.

More Doppler effect problems