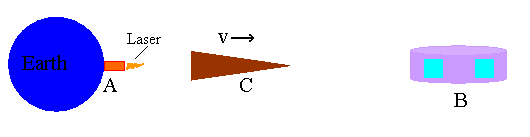The Doppler shift

Problem:

Derive the expression for the Doppler shift, ω' = γω(1 - (v/c)cosθ), by applying the Lorentz transformation to the momentum 4-vector of a photon.

Solution:

• Concepts:
  The Doppler shift, the Lorentz transformation of the momentum 4-vector of a photon
• Reasoning:
  In reference frame K let orient the coordinate system so that the photon moves in the xy-plane, its trajectory making an angle θ with the x-axis.
  Let reference frame K' move with velocity v/c = β in the positive x direction with respect to K.
  Then the Lorentz transformation of the momentum 4-vector of the photon from frame K to frame K' can be written as
  .
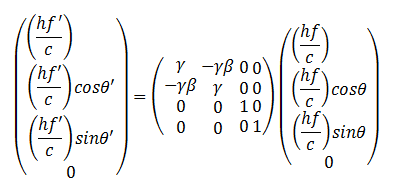• Details of the calculation:
  We find hf'/c = γ(hf/c) - γβ(hf/c)cosθ,  f' = γf(1 - βcosθ), ω' = γω(1 - (v/c)cosθ), since ω = 2πf.

Problem:

Let reference frame K' move with velocity v with respect to reference frame K.  In K a sinusoidal electromagnetic plane wave has an angular frequency ω and a wave vector k.  Find ω' and k' in reference frame K'.

Solution:

• Concepts:
  The Doppler shift
• Reasoning:
  We are asked to derive the relativistically correct expression for the Doppler shift.
• Details of the calculation:
  If we picture the wave as a series of crests and troughs moving through space, then the phase of any labeled point is a relativistically invariant quantity.  Observers in K and K' will agree on the phase of the a labeled point, i.e. they will agree if the point is on a crest, in a trough, etc.
  We label the phase by Φ = k·r-ωt = k'·r'-ω't'.
  Let  ω = k₀c, then k₀ct - k·r = k₀'ct' - k'·r',  (k₀,k)·(ct,r) = ( k₀',k')·(ct',r') for any 4-vector (ct,r).  The dot product of (k₀,k) with any 4-vector yields a Lorentz invariant quantity.  Therefore (k₀,k) is itself a 4-vector.
  Since (k₀,k) is a 4-vector, we know how it transforms under a Lorentz transformation.
  With β = v/c, |k| = k₀ = ω/c, and  β·k = (vω/c²)cosθ, where θ is the angle between the directions of v and k, we have
  k₀' = γ(k₀ - β·k) = γ(k₀ - (vω/c²)cosθ) ,
  k'_|| = (k_|| - βk₀) = (k_|| - vω/c²),
  k'_⊥ = k_⊥.
  Since ω' = k₀'c we have
  ω' = γ(ω - v·k) = γω(1 - vcosθ/c).
  ω' = ω[(1 - v/c)/(1 + v/c)]^½ if k and v are parallel to each other.
  ω' = ω[(1 + v/c)/(1 - v/c)]^½ if k and v are anti-parallel to each other.
  ω' = γω if k and v are perpendicular to each other.
  There is a transverse Doppler shift, even if θ = π/2.

Problem:

Reference frame K' moves with velocity vi with respect to reference frame K.  An electromagnetic plane wave is observed in K propagating in a direction -i + j with frequency ν.   Find the frequency and direction of propagation of the plane wave when it is observed in K'.

Solution:

• Concepts:
  The Doppler shift, the Lorentz transformation of the (k₀,k) 4-vector
• Reasoning:
  If we picture the wave as a series of crests and troughs moving through space, then the phase of any labeled point is a relativistically invariant quantity.  Observers in K and K' will agree on the phase of the a labeled point, i.e. they will agree if the point is on a crest, in a trough, etc.
  We label the phase by φ = k·r - ωt = k'·r' - ω't'.
  Let  ω = k₀c, then k₀ct - k·r = k₀'ct' - k'·r',  (k₀,k)·(ct,r) = ( k₀',k')·(ct',r') for any 4-vector (ct,r).  The dot product of (k₀,k) with any 4-vector yields a Lorentz invariant quantity.  Therefore (k₀,k) is itself a 4-vector.
  The angular frequency ω of a sinusoidal electromagnetic wave with wave vector k (k = 2π/λ = ω/c) in a reference frame K is measured as ω' in a reference frame K' moving with uniform velocity v with respect to K.
  ω' = γω(1 - (v/c)cosθ), where θ is the angle between the directions of k and v.
  In frame K we have tanθ  = k_y/k_x.  In frame K' we have tanθ'  = k_y'/k_x'.  We find k_y' and k_x' by transforming the (k₀,k) 4-vector.  Here k₀ = ω/c and |k| = 2π/λ = ω/c.
• Details of the calculation:
  θ = 135^o is the angle k makes with the x-axis.  The frequency of the plane wave in K' is ν' = γν(1 + v/(2^½c)).
  The Lorentz transformation of the (k₀,k) 4-vector yields
  
  .

  tanθ'  = k_y'/k_x' = -1/[γ(β√2  + 1)] is the angle the wave vector makes with the x-axis in K'.  θ' defines the direction of propagation of the plane wave in K'.

Problem:

A source emits electromagnetic waves with frequency f into a 4π solid angle.  What is the frequency f' of the waves observed by an observer moving with speed v in a circular orbit around the source?

Solution:

• Concepts:
  Transverse Doppler shift
• Reasoning:
  The time interval between successive crests reaching the observer as seen in the rest frame of the source is T.  In the frame of the observer it is the proper time interval t = T/γ.  We have t < T, f' > f.  It is only the instantaneous velocity which is important in calculating the time dilation.
• Details of the calculation:
  Let k be the wave vector and v the relative velocity;
  f' = γf if k and v are perpendicular to each other.

Problem:

A star is moving towards the earth at a speed of 3 * 10⁶ m/s.  This speed was determined by observing that the wavelength of a particular spectral line was shifted by 1 nm.
(a) What is the wavelength of the spectral line that must have been used for this measurement?
(b) Was the shift towards shorter or longer wavelengths?
(c) When observing a different star from earth, the frequency for that particular line is observed to have increased by 80%.  How fast is that star moving relative to earth?
(d) Is it moving towards or away from Earth?

Solution:

• Concepts:
  Doppler shift
• Reasoning:
  When observer and source are in relative motion, the frequency of spectral lines is different in the source and the observer frame.
  Doppler shift: f' = γf(1 - (v/c)cosθ), where θ is the angle between the directions of v and k.
• Details of the calculation:
  (a)  θ = 0^o.  f' = f[(1 + v/c)/(1 - v/c)]^½ = αf.  α = 1.01.
  λ - λ' = λ(α - 1)/α = 10^-9 m.  λ = 101 nm.
  (b)  The shift was towards shorter wavelength.
  (c)  f' = 1.8 f = f[(1 + v/c)/(1  -v/c)]^½.  v/c = 0.53.
  (d)  The star is moving towards Earth.

Problem:

Light from Sirius A shows a shift in wavelength due to the influence of a companion star, Sirius B, with a period of 50 years.
(a)  If the Balmer α line of hydrogen  (λ_rest =  656 nanometers) exhibits a maximum Doppler shift of 0.025 nm, what is the orbital velocity of Sirius A?
(b)  Given this orbital velocity, what is the radius of Sirius's orbit, if one assumes a circular orbit?
(c)  What is the combined mass of Sirius A and Sirius B?

Solution:

• Concepts:
  Doppler shift, orbiting
• Reasoning:
  Let us assume we are viewing the orbit edge on.  The maximum Doppler shift of the α line of hydrogen yields v,  v = 2πr/T yields the orbital radius of Sirius A.
• Details of the calculation:
  (a)  Assume a blue shift.  The star is approaching Earth, f' > f.  f'/f = [(1 + v/c)/(1 - v/c)]^½. 
  If v << c and Δf << f, then | Δf/f| = | Δλ/λ| = v/c.
  Here v/c = 0.025/656 = 3.81*10^-5, v = 11433 m/s.
  (b)  v = 2πr/T,  r = vT/(2π) = 2.87*10¹² m.
  (c)  Solve for the relative motion of two interacting masses m₁ and m₂ by solving for the motion of one fictitious particle of reduced mass μ = m₁m₂/(m₁ + m₂) in a central field.
  The fictitious particle moves in a circular orbit of radius r.
  F = Gm₁m₂/r² =( m₁m₂/(m₁ + m₂))v²/r,   m₁ + m₂ = v²r/G = 5.62*10³⁰ kg

Problem:

A, located on earth, signals with a laser pulse every six minutes.  B is on a space station that is stationary with respect to earth.  C is in a rocket traveling from A to B with a velocity v = 0.6c relative to A.

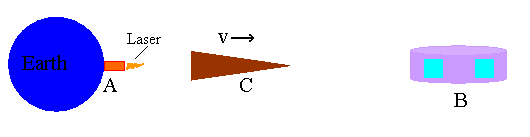
(a)  At what intervals does B receive signals from A?
(b)  At what intervals does C receive signals from A?
(c)  If C reflects light pulses back to A, at what intervals does A receive these pulses?

Solution:

• Concepts:
  The Doppler shift
• Reasoning:
  We are given the frequency of a signal in one inertial frame and are asked to find it in another inertial frame.
  f' = f[(1 - v/c)/(1 + v/c)]^½ if the two frames recede from each other.
• Details of the calculation:
  (a)  B receives a signal every six minutes.
  (b)  f' = f[(1 - 0.6)/(1 + 0.6)]^½ = 0.5 f,  T' = 2T, C receives a signal every 12 minutes.
  (c)  f'' = 0.5 f' = 0.25 f, since A recedes from C with speed v.  A receives a pulse every 24 minutes.

Problem:

The relativistic Doppler effect is the change in frequency f of light, caused by relative motion of the source and the observer.  Assume that the source and the observer are moving away from each other with a relative velocity v.  Consider the problem in the reference frame of the source.  Let f_s be the frequency of the wave the source emits.  Suppose one wave front arrives at the observer.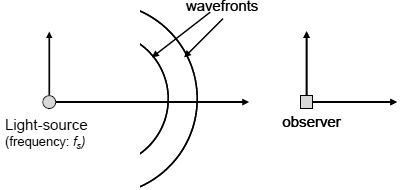
(a)  What is the distance of the next wave front away from him?
(b)  What is the time t between crest (of the wave front) arrivals at the observer?
(c)  Due to relativistic effect, what will the observer measure this time t₀ to be?
(d)  What is the corresponding observed frequency f₀?

Solution:

• Concepts:
  The Doppler shift, time dilation
• Reasoning:
  In vacuum, light moves with speed c in every reference frame.
• Details of the calculation:
  (a)  In the reference frame of the source, the next wave front is a distance λ away from the observer, but it has to travel a distance λ + d to reach the observer after time t..
  c = (λ + d)/t, v = d/t, d/v = (λ + d)/c, d = λv/(c - v) = (1/f)cv/(c - v).
  (b) t = d/v = (1/f)c/(c - v) = (1/f)c/(c - v) = 1/[f(1 - v/c)]
  (c) t' = τ = t/γ = proper time.
  t' = (1 - v²/c²)^½/[f(1 - v/c)] = (1/f)[1 + v/c)/(1 - v/c)]^½.
  (d) t' = 1/f₀,  f₀ = f [1 - v/c)/(1 + v/c)]^½.

Problem:

An excited nucleus of ⁵⁷Fe formed by the radioactive decay of ⁵⁷Co emits a gamma ray of 1.44 *10⁴ eV.  In the process, there is conservation of energy and m₀c² = γm_a0c² + hf,  where m₀c² is the initial mass of the nucleus and m_a0c² is its mass after the emission of the gamma ray.  There is also conservation of momentum, hf/c = γm_a0u, where u is the recoil velocity of the iron nucleus.  The energy released by the reaction is E_r = (m₀ - m_a0)c².
(a)  Show that  hf = E_r(m₀ + m_a0)/(2m₀) = (1 - E_r/(2m₀c²))E_r.
Thus hf < E_r: part of E_r goes to the photon, and the other part supplies kinetic energy to the recoiling nucleus.

(b)  Set m₀ = 57*1.7*10^-27 kg, and show that E_r/(2m₀c²)) ~ 1.3*10^-7.
Thus the fraction of the available energy E_r that appears as recoil is small.

(c)  Moessbauer discovered in 1958 that, with solid iron, a significant fraction of the atoms recoil as if they were locked rigidly to the rest of the solid.  This is the Moessbauer effect.  If the sample has a mass of 1 gram, by what fraction is the gamma ray energy shifted in the recoil process?

(d)  A sample of normal ⁵⁷Fe absorbs gamma rays of 14.4 keV by the inverse recoilless process much more strongly than it absorbs gamma rays of any nearby energy.  The excited nuclei thus formed reemit 14.4 keV radiation in random directions some time later.  This is resonant scattering.  If a sample of activated ⁵⁷Fe moves in the direction of a sample of normal ⁵⁷Fe, what must be the value of the velocity v that will shift the frequency of the gamma rays, as seen by the normal nuclei, by 3 parts in 10¹³?  This is one line width.

(e)  A Doppler shift in the gamma ray results in a much lower absorption by a nucleus if the shift is of the order of one line width or more.  What happens to the counting rate of a gamma-ray detector placed behind the sample of normal ⁵⁷Fe when the source of activated Fe moves
    (i) toward the normal ⁵⁷Fe,
    (ii) away from it?

(f)  If a 14.4 keV gamma ray travels 22.5 meters vertically upward, by what fraction will its energy decrease?
[Gravitation redshift, a thought experiment:  Suppose a particle of rest mass m is dropped from the top of a tower and falls freely with acceleration g.  It reaches the ground with a velocity v = (2gh)^1/2, so its total energy E, as measured by an observer at the foot of the tower is E = mc² + ½mv² + O(v⁴) = mc² + mgh + O(v⁴).
Suppose an observer has some magical method of converting all this energy into a photon of the same energy.  Upon its arrival at the top of the tower with energy E the photon is again magically changed into a particle of rest mass m' = E'/c. Energy conservation requires that m' = m. 
Therefore E'/E = mc²/(mc² + mgh + O(v⁴)) = (1 + gh/c² + O(v⁴))^-1 = 1 - gh/c² + O(v⁴).]

(g)  A normal ⁵⁷Fe absorber located at this height must move in what direction and at what speed in order for resonant scattering to occur?

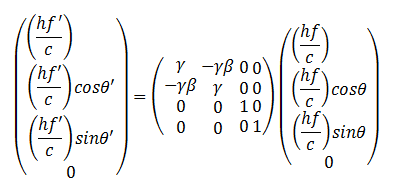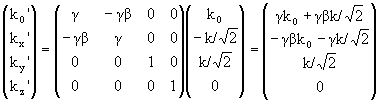More Doppler effect problems