The transformation of the force

Problem:

An observer in the laboratory observes a beam of electrons with charge density ρ moving at velocity v = vk.  If the beam has circular radius R find the repulsive force acting on an electron inside the beam (r < R) both with respect to the rest frame of the electrons and with respect to the observer in the laboratory frame, respectively.

Solution:

• Concepts:
  The Lorentz force, the Lorentz transformation
• Reasoning:
  Because of the cylindrical symmetry we can find the electric and magnetic fields from Gauss' law and Ampere's law respectively.  We can then find the force F = q(E + v×B) on an individual particle with charge q.
• Details of the calculation:
  In the laboratory frame at r < R:  E = ρr/(2ε₀), the direction of E is radial inward.
  B = μ₀ρrv/2, the direction of B is the -φ direction.
  The force on the electron has magnitude F = [q_eρr/(2ε₀)](1 - v²/c²), pointing radially outward.

  In the rest frame of the electron F' = q_eρ'r'/(2ε₀), radially outward.
  The Lorentz transformation of the 4 vector current to a frame moving with β = (v/c)k with respect to the lab frame yields
  cρ' = γ(cρ - βρv),  ρ' = ργ(1 - v²/c²)  = ρ(1 - v²/c²)^½. 
  F' = [q_eρr/(2ε₀)](1 - v²/c²)^½, since r' = r.
  or
  F' = dp'_⊥/dt' = dp'_⊥/dτ in the rest frame of the electron
  F' = dp_⊥/dτ = γdp_⊥/dt = γF,  since p is a 4-vector and p'_⊥ = p_⊥.

Problem:

An electric field E exerts a force F = qE on a charge q at rest.  Show that the expression for the Lorentz force follows directly from the Lorentz transformation properties of the fields.

Solution:

• Concepts:
  The Lorentz transformation of the electromagnetic fields, the Lorentz force
• Reasoning:
  We are asked to derive the expression for the Lorentz force from the transformation properties of the fields.  The Lorentz force is the force exerted by electromagnetic fields on a charge moving with velocity v.
• Details of the calculation:
  let K be the frame in which the charge is at rest.
  In K we have external fields E and B and the force on the charge is F = qE.
  In K' we observe an electric field E' and a magnetic field B'.
  We have from the Lorentz transformation of the fields
  E_|| = E'_||,  B_|| = B'_||,  E_⊥ = γ(E' + v×B')_⊥,  B_⊥ = γ(B' - (v/c²)×E')_⊥.
  In K the force on the charge is F = dp/dt = dp/dτ, where τ is the proper time, a Lorentz invariant.
  In K' the force on the charge is F' = dp'/dt' = (1/γ)dp'/dt, γF' = dp'/dτ.
  Here   γ = (1 - β²)^-½, β = v/c.
  From the transformation properties of the momentum 4-vector
  p^μ = (γmc,γmv) = (E_k/c,p) = under a Lorentz transformation,
  p'_|| = γ(p_|| + βE_k/c), p'_⊥ = p_⊥, we have
  γF'_⊥ = dp'_⊥/dτ  = dp_⊥/dτ  = dp_⊥/dt = qE_⊥ = γq(E' + v×B')_⊥.
  F'_⊥ = q(E'_⊥ + v×B').
  (Note: we use E_k to distinguish energy from the magnitude of the electric field.)
  γF'_|| = dp'_||/dτ = γdp_||/dτ = γdp_||/dt = γqE_|| = γqE'_||.
  F'_|| = qE'_||.
  We have used that in K d(E_k/c)/dt  = (1/c)dE_k/dt = 0 since in K the charge is at rest.
  [E_k = mc²/(1 - u²/c²)^½,  dE_k/dt = [m/(1 - u²/c²)^3/2] udu/dt = 0 if u = 0.]
  Therefore F' = q(E' + v×B').  This is the expression for the Lorentz force.

Problem:

At t = 0 a particle with mass m and negative charge -q leaves the origin with a relativistic velocity v = v₀k.  It moves in a region with  E = E₀k,  B = 0.   When does it return to the origin?  What is its maximum distance from the origin?  Neglect radiation.

Solution:

• Concepts:
  Relativistic dynamics
• Reasoning:
  The particle may move with relativistic speed.
  F = dp/dt.  Energy = (m²c⁴ + p²c²)^½ = γmc²,  p = γmv.
• Details of the calculation:
  dp/dt = -qE,  p_z(t) = p₀ - qE₀t,  p_x(t) = p_y(t) = 0.
  At the highest point p_z(t) = 0, t = p₀/qE₀.  The particle returns to the origin at t = 2p₀/qE₀. 
  The particle returns at t = 2γ₀mv₀/(qE₀) = 2(1 - v₀²/c²)^-½mv₀/qE₀.
  The maximum distance from the origin is z_max.
  z_max = ∫₀^p0/qE0 v dt.  v/c = pc/E = (p₀ - qE₀t)/(m²c² + (p₀ - qE₀t)²)^½ .
  z_max = (c/qE₀)∫₀^p0 y dy/(m²c² + y²)^½
  = (1/qE₀)[(m²c⁴ + p₀²c²)^½ - mc²]
  = (γ₀ - 1)mc²/(qE₀) = mc²/(qE₀) [(1 - v₀²/c²)^-½ - 1].
  or,
  U(z_max) = qE₀z_max.  E = mc² + qE₀z_max = γ₀mc².  (energy conservation)
  z_max =  (γ₀ - 1)mc²/(qE₀) = mc²/(qE₀) [(1 - v₀²/c²)^-½ - 1].

Problem:

Two electric charges, q₁ and q₂, are moving with the same velocity V.  Let R be the vector pointing from q₂ to q₁, and let θ be the angle between R and V.  The speed V is not small compared to the speed of light.  Find the force q₂ exerts on q₁ in this coordinate system (the lab frame).  Give all the components of the force vector.  Assume that the charges are moving in the xy-plane, and that the positive x-direction is the direction of motion.

Solution:

• Concepts:
  The Lorentz transformation
• Reasoning:
  We can calculate the force between the charges in the rest frame of the charges from F = qE and transform this force to the laboratory frame, or we can calculate the electric field of one of the charges in its rest frame, transform it into and electric and magnetic field in the laboratory frame, and calculate the force between the charges from F = q(E + v×B).
• Details of the calculation:
  In the lab frame R² = (Δx)² + (Δy)², Δx = Rcosθ, Δy = Rsinθ.
  
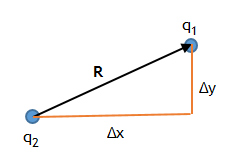
  The rest frame of the two charges moves with respect to the lab frame with velocity Vi. 
  The lab frame moves with respect to the rest frame with velocity -Vi. 
  In the rest frame of the charges R'² = (Δx')² + (Δy')², Δx' = γRcosθ, Δy' = Rsinθ.
  Here   γ = (1 - β²)^-½, β = V/c.
  R'² = γ²((Δx)² + (Δy)²/γ²) = γ²R²(cos²θ + sin²θ/γ²)
  = γ²R²(1 - sin²θ + (1 - β²)sin²θ) = γ²R²(1 - β²sin²θ).
  Method 1:
  In the rest frame of the charges let F' denote the force q₂ exerts on q₁.
  F'_x = (kq₁q₂/R'²)(Δx'/R'),  F'_y = (kq₁q₂/R'²)(Δy'/R').
  F' = dp'/dt' = dp'/dτ, where τ is the proper time, a Lorentz invariant.
  In the lab frame the force on q₁ is F = dp/dt = (1/γ)dp/dτ, γF = dp/dτ.
  From the transformation properties of the momentum 4-vector p^μ = (γmc,γmv) = (E/c,p) under a Lorentz transformation,
  p_||= γ(p'_|| + βE'/c), p_⊥ = p'_⊥, we have
  γF_y = dp_y/dτ  = dp'_y/dτ  = dp'_y/dt' = (kq₁q₂/R'²)(Δy'/R'), F_y = (1/γ)(kq₁q₂/R'²)(Δy'/R').
  F_y = (1/γ)(kq₁q₂Rsinθ/(γ²R²(1 - β²sin²θ))^3/2 =  (kq₁q₂sinθ/R²)(1 - β²)²/(1 - β²sin²θ)^3/2.
  γF_x = dp_x/dτ  = γdp'_x/dτ  = γdp'_x/dt'  =  γ(kq₁q₂/R'²)(Δx'/R')
  We have used that in K' d(E'/c)/dt'  = (1/c)dE'/dt' = 0 since K' is the rest frame of the charges.
  F_x = (kq₁q₂/R'²)(Δx'/R') = (kq₁q₂cosθ/R²)(1 - β²)/(1 - β²sin²θ)^3/2.
  Summary: 
  F_y = (kq₁q₂sinθ/R²)(1 - β²)²/(1 - β²sin²θ)^3/2,
  F_x = (kq₁q₂cosθ/R²)(1 - β²)/(1 - β²sin²θ)^3/2.
  
  Method 2:
  In the rest frame of the charges let E' and B' denote the fields produced by q₂ at the location of q₁.
  E'_x = (kq₂/R'²)(Δx'/R'),  E'_y = (kq₂/R'²)(Δy'/R').  B' = 0.
  Transformation properties of the fields:
  E_|| = E'_||,  B_|| = B'_||,  E_⊥ = γ(E' + v×B')_⊥,  B_⊥ = γ(B' - (v/c²)×E')_⊥.
  Here E_x = E_x' = (kq₂/R'²)(Δx'/R') = (kq₂cosθ/R²)(1 - β²)/(1 - β²sin²θ)^3/2.  B_x = 0.
  E_y = γE'_y = γ(kq₂/R'²)(Δy'/R') =  (kq₂sinθ/R²)(1 - β²)/(1 - β²sin²θ)^3/2.
  B_y = 0,  B_z = γ(β/c)(kq₂/R'²)(Δy'/R') = (β/c)(kq₂sinθ/R²)(1 - β²)/(1 - β²sin²θ)^3/2
  F_x = q₁E_x = (kq₁q₂cosθ/R²)(1 - β²)/(1 - β²sin²θ)^3/2.
  F_y = q₁E_y - VB_z = (kq₁q₂sinθ/R²)(1 - β²)/(1 - β²sin²θ)^3/2 - β²(kq₂sinθ/R²)(1 - β²)/(1 - β²sin²θ)^3/2.
  F_y = (kq₁q₂sinθ/R²)(1 - β²)²/(1 - β²sin²θ)^3/2.

Problem:

An aluminum disk of radius R, thickness d, conductivity σ and mass density ρ is mounted on a frictionless vertical axis.  It passes between the poles of a magnet near its rim, which produces a B field perpendicular to the plane of the disk over a small area A of the disk.  If the initial angular speed of the disk is Ω₀, how many revolutions will it make before it comes to rest?

Solution:

• Concepts:
  The Lorentz transformation of the electromagnetic fields, the Lorentz force
• Reasoning:
  Even at non-relativistic speeds, problems involving Eddy currents are often easier analyzed after a frame transformation.
• Details of the calculation:
  
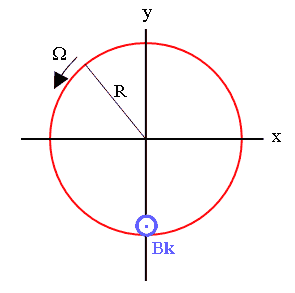
  In the laboratory frame K, the magnetic field B = Bk is perpendicular to the disk over a small area A.  Consider an observer passing through the region of the magnetic field with speed v = ΩRi.  In this observer's rest frame K' there exists an electric field E'_⊥ = γ(E + v×B)_⊥ = -γvBj.
  All velocities are non-relativistic, so  γ ~ 1 and E'_⊥ ~ -vBj = -ΩRBj.
  There also exist a magnetic field B'_⊥ = γB_⊥ ~ Bk.
  In K' the current density is  j_c' = σE' = -σΩRBj and the Lorentz force on the small volume ΔV = Ad is
  F' = j_c'×B' ΔV = -σΩRB²Adi.  Because γ ~ 1, the force F observed in the laboratory frame is equal to F'.
  In the laboratory frame F produces a torque about the axis of rotation.
  τ = -Rj×F = -σΩR²B²Adk.
  The moment of inertia of the disk is I = ½MR² = ½ρdπR⁴.
  The equation of motion is τ_z = IdΩ/dt or -σΩR²B²Ad = ½ρdπR⁴dΩ/dt.
  dΩ/dt = -Ω2σB²A/(ρπR²).  Ω(t) = Ω₀exp(-2σB²At/(ρπR²)).
  The number of revolutions the disk makes before it comes to rest is
  N = θ_tot/2π = (½π)∫₀^∞Ω(t)dt = (Ω₀/2π)∫₀^∞exp(-2σB²At/(ρπR²))dt = (Ω₀ρR²/4σB²A).

Problem:

A line of charge with charge density λ C/m is fixed at rest along the x' axis of a reference frame S'.  A test charge q is at rest in S' at (0, 0, z' = d).  S' is in constant motion with velocity v = vi with respect to a reference frame S.
(a)  Calculate the electric field of the line of charge in the rest frame S' and the force on q. 
(b)  Calculate the electric and magnetic fields of the line of charge measured by an observer at rest in S.
(c)  Calculate the force measured by the observer in S on the test charge q.