Newton's 2nd law

Problem:

Two masses (m₁ = 15 kg and m₂ = 20 kg) are connected by a massless cord and placed on a horizontal, frictionless surface.  The two-mass system is pulled to the right by a force F_A = 60 N using a cord that makes an angle of 40 degrees with the horizontal.  The masses remain on the horizontal surface.  There is no vertical motion.

(a)  Draw the free body diagrams for the two masses, properly labeling all forces.
(b)  What is the normal force between mass m₂ and the horizontal surface?
(c)  What is the acceleration of the system?
(d)  What is the tension F_T in the cord between the two masses?

Solution:

• Concepts:
  Newton's laws
• Reasoning:
  Newton's laws are well suited for the study of unconstrained mechanical systems. 
• Details of the calculation:
  (a)
   
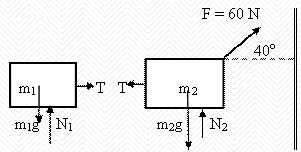
  (b)  F_x = 45.9 N,  F_y = 38.6 N.  N₂ = m₂g - F_y = 157.4 N.
  (c)  a = F_x/(m₁ + m₂) = 1.31 m/s².
  (d)  F_T = m₁a = 19.7 N.

Problem:

A free particle with mass m is subjected to a time-dependent force F(t) = F₀ exp(-t/τ) for t > 0.  F₀ and τ are constants.
(a)  Find the velocity v(t) of the particle as a function of time, given that v = 0 at time t = 0.
(b)  What is the total work done on the particle by the force as t --> infinity?

Solution:

• Concepts:
  Newton's 2^nd law, the work-kinetic energy theorem
• Reasoning:
  Given the acceleration and v(0) we can find v(t) and the kinetic energy at time t.  The net work done on the object is equal to the change in the kinetic energy of the object.
• Details of the calculation:
  (a)  F = ma = mdv/dt = F₀ exp(-t/τ), v(t) = (F₀τ/m)(1 - exp(-t/τ)).
  (b)  As t --> infinity, v --> F₀τ/m.
  Total work done by the force: W = ½mv_inf² = ½(F₀τ)²/m.

Problem:

A 36 g bullet with a speed of 350 m/s strikes a 8 cm thick fence post.  The bullet is retarded by an average force of 3.6*10³ N while traveling all the way through the board.
(a)   What speed does the bullet have when it emerges?
(b)   How many such boards could the bullet penetrate?