Inelastic collisions

Collisions in 1D

Problem:

A particle of mass m₁ and velocity u₁ collides with a particle of mass m₂ at rest.  The two particles stick together.  What fraction of the original kinetic energy is lost in the collision?  (Simplify the answer as much as possible.)

Solution:

• Concepts:
  Momentum conservation
• Reasoning:
  In an inelastic collision kinetic energy is not conserved, but momentum is conserved.
• Details of the calculation:
  m₁u₁ = (m₁ + m₂)v.
  E_f = ½ (m₁ + m₂)v²,  E_i = ½ m₁u₁².
  Fraction of energy lost = (E_i - E_f)/E_i = 1 - m₁/(m₁ + m₂) = m₂/(m₁ + m₂).

Problem:

A particle of mass m traveling with (non-relativistic) velocity u₁ makes a head-on collision with a second particle of mass M, which is at rest in the laboratory.  If the collision is completely inelastic, what fraction of the original kinetic energy remains after the collision?

Solution:

• Concepts:
  Inelastic collisions, momentum conservation
• Reasoning:
  In inelastic collisions: momentum is conserved, mechanical energy is not conserved.
• Details of the calculation:
  Assume the particle is initially traveling in the positive x-direction.
  Before the collision: p_i = mu₁, E_i = ½mu₁².
  After the collision: p_f = (m+M)v = mu₁.  E_f = ½(M+m)v² = ½[m²/(M+m)]u₁².
  E_f/E_i = m/(M+m).

Problem:

A 36 g bullet with a speed of 350 m/s strikes a 8 cm thick fence post.  The bullet is retarded by an average force of 3.6*10³ N while traveling all the way through the board.
(a)   What speed does the bullet have when it emerges?
(b)   How many such boards could the bullet penetrate?

Solution:

• Concepts:
  Newton's second law, F = ma, motion with constant acceleration in one dimension
• Reasoning:
  For motion with constant acceleration the equations of kinematics yield 
  v_xf² = v_xi² + 2a_x(x_f - x_i).
• Details of the calculation:
  (a)  (x_f - x_i) = 0.08 m, v_xf² = (350 m/s)² - 2*(0.08 m)(3.6*10³ N)/( 36*10^-3  kg), 
  v_xf  = 326.34 m/s.
  (b)  v_xf  = 0,  (350 m/s)² = 2*d(3.6*10³ N)/( 36*10^-3  kg), d = 0.6125 m.
  # of boards the bullet can penetrate = 7, (d/0.08 = 7.65)
  or
  Work-kinetic energy theorem:  <F>d = ½mv_i².

Problem:

Board A is placed on board B as shown.  Both boards slide, without moving with respect to each other, along a frictionless horizontal surface at a speed v.  Board B hits a resting board C "head-on."  After the collision, boards B and C move together, and board A slides on top of board C and stops its motion relative to C in the position shown on the diagram.  What is the length of each board?  All three boards have the same mass, size, and shape.  It is known there is no friction between boards A and B; the coefficient of kinetic friction between boards A and C is μ_k.

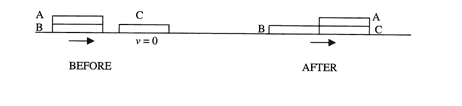
Solution:

• Concepts:
  Inelastic collisions, momentum conservation, friction
• Reasoning:
  Board B and C collide inelastically.  Board A slides over boards B and C, and we have sliding friction.  Solve the problem in a inertial frame.
• Details of the calculation:
  After the collision boards B and C stick together and move with speed v/2 in the lab frame (momentum conservation).  There is no friction between A and B.  Board A moves with speed v in the lab frame.  The CM frame moves with velocity 2v/3 towards the right.  In the CM frame board A moves with velocity v/3 towards the right and boards B and C move with velocity v/6 towards the left right after the inelastic collision.  Let us work in that frame.  Let the right edge of board A be at x' = 0 at t = 0, right after the collision.  At time t, when the right edge of the board A is at x', the force on the board is the force of friction μN = μmg3x'/(2L) directed towards the left.
  L is the length of each board, 3x'/(2L) represents the fraction of the top board that is supported by the surface with friction.
  The acceleration is a = F/m, d²x'/dt² = -μg3x'/(2L).
  The solution to this differential equation is
  x' = x'₀sinωt, ω = (3μg /(2L))^½, v' = ωx'₀cosωt,
  with the initial conditions
  x'(0) = 0, v'(0) = v/3 = ωx'₀.
  x'₀ = v/(3ω) = v'(0)/(3μg/(2L))^½.
  When x' = x'₀, v' = 0.  x'₀ therefore is the (2/3) of length of the board, x'₀ = 2L/3.
  2L/3 = v'(0)/(3μg/(2L))^½, 2L²/9 = v'(0)²L/(3μg).
  The length of the board is L = 3v'(0)²/(2μg) = v²/(6μg)
  
  You can also use the work-kinetic energy theorem.  We have in the CM frame
  F = -Cx', C = 3mμg/(2L).  C(2L/3)²/2 = ½m(v/3)², L = v²/(6μg).

Problem:

An hour glass sits on a scale.  Initially all the sand (mass m) in the glass (mass M) is held in the upper reservoir.  At t = 0, the sand is released.  If it exits the upper reservoir at a constant rate dm/dt = -λ, draw (and label quantitatively) a graph showing the reading of the scale at all times t > 0.

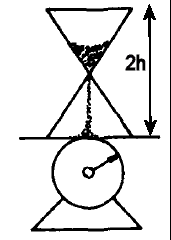
Solution:

• Concepts:
  Newton's 2nd law, F = dp/dt
• Reasoning:
  The reading of the scale is determined by the amount of sand not falling freely and the force required to reduce the momentum of an amount of sand dm reaching the bottom to zero in the a time interval dt.
• Details of the calculation:
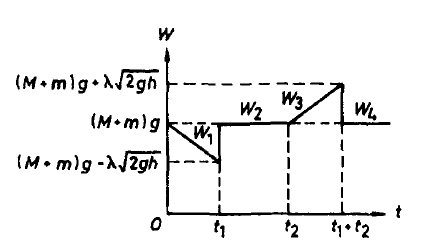
  Each grain of sand falls a distance h. 
  It therefore falls for a time interval t₁ = (2h/g)^½.  The first grain hits the bottom at t = t₁.
  For 0 < t < t₁, the scale reads W₁ = (M + m)g - λgt.
  W₁ decreases linearly from (M + m)g to (M + m)g - λ(2gh)^½.
  
  At time t₂ = m/λ, all the sand has left the upper reservoir.  
  For t₁ < t < t₂, W₂ = (M + m)g - λgt₁ + v|dm/dt|.
  (M + m)g - λgt₁ is the weight of the sand that is not falling and v|dm/dt| is the force required to reduce the momentum of the amount of sand |dm| = λdt reaching the bottom in the time interval dt with speed v = (2gh)^½ to zero in the time interval dt.
  v|dm/dt| = (2gh)^½λ.  λgt₁ = λg(2h/g)^½ = (2gh)^½λ.
  Therefore W₂ = (M + m)g.  W₂ is constant.
  
  At time t₃ = t₂ + t₁ all the sand has reached the bottom.  For t₂ < t < t₃, W₃ = W₂ +  λg(t - t₂) .
  W₃ increases linearly from (M + m)g to (M + m)g + λ(2gh)^½.
  
  For t > t₃, W₄ = (M + m)g = constant.
  

Problem:

A 15.2 g bullet hits a 0.463 kg block from below.  The initial speed of the bullet is 624 m/s and it emerges from the block at 131 m/s.
(a)  How high does the block rise?
(b)  If the block is 2.34 cm thick, estimate the average force on the block.  Assume that the bullet passes completely through before the block moves appreciably.

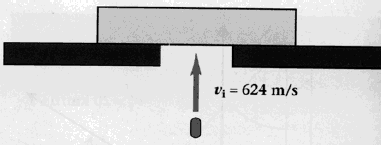
Solution:

• Concepts:
  Momentum conservation, impulse
• Reasoning:
  In the collision between the bullet and the block momentum is conserved.  The collision time is very short.
  This is a 1-dimensional problem.
• Details of the calculation:
  (a)  m = 0.0152 kg , M = 0.463 kg, mv_i = mv_f + Mv.
  v = m(v_i - v_f)/M = 0.0152*(489 m/s)/ 0.463 = 16 m/s.
  The initial speed of the block is v = 16 m/s.
  It rises to a height h = v²/(2g) = 13.15 m.
  (b)  The block receives an impulse Δp = Mv in the time interval Δt.
  Δt is the time it takes the bullet to pass through the block,
  Δt = 2*(0.0234 m)/(v_i + v_f) = 6.23*10^-5 s, assuming uniform deceleration.
  F = Δp/Δt = 1.19*10⁵ N.

Collisions in 2D

Problem:

A particle of mass m strikes a frictionless, smooth, hard surface at an angle θ from the surface normal.  The particle bounces off with coefficient of restitution ε.  (The coefficient of restitution is defined as the ratio of the magnitudes of the velocity components along the normal to the plane of contact after and before the collision.)  Find the rebound angle for the particle as it leaves the surface.

Solution:

• Concepts:
  Definition: coefficient of restitution
• Reasoning:
  This is an inelastic collision.  We are asked to find the rebound angle when given the coefficient of restitution.
• Details of the calculation:
  ε = |v₂|/|v₁|, v₁ is the velocity component of the particle toward the floor before collision and v₂ is the velocity component of the particle away from the floor after the collision.
  Before the collision: tanθ = |v_x|/|v_y|.
  After the collision: tanθ' = |v_x'|/|v_y'| = |v_x|/(ε|v_y|) = (1/ε)tanθ.
  Since ε < 1, the rebound angle is bigger than the incoming angle.

Problem:

A 90 kg fullback running east with a speed of 5 m/s is tackled by a 95 kg opponent running north with a speed of 3 m/s.  If the collision is perfectly inelastic, calculate the speed and the direction of the players just after the tackle.

Solution:

• Concepts:
  Inelastic collision, conservation of momentum
• Reasoning:
  If a component of the total external force acting on a system is zero, then the corresponding component of the total momentum is conserved.  We assume that the horizontal component of the external force can be neglected during the collision.
• Details of the calculation:
  The initial momentum of player 1 is p₁ = (90 kg 5 m/s)i = (450 kgm/s)i.
  The initial momentum of player 2 is p₂ = (95 kg 3 m/s)j = (285 kgm/s)j.
  Momentum is conserved, the final momentum p of both players is p = p₁ + p₂.
  p = (m₁ + m₂)v.
  v = (2.432 m/s)i + (1.54 m/s)j.
  v² = 8.29(m/s)², v = 2.88 m/s.
  The speed of the players after the collision is 2.88 m/s.
  tanθ = p_y/p_x = 285/450 = 0.63, θ = 32.34^o.
  Their direction of travel makes an angle θ= 32.34^o with the x-axis.  (The x-axis is pointing east.)

Problem:

After a completely inelastic collision between two objects of equal mass, each having initial speed v, the two move off together with speed v/3.  What was the angle between their initial directions?

Solution:

• Concepts:
  Conservation of momentum
• Reasoning:
  The external force acting on the system is zero, the total momentum is conserved.
• Details of the calculation:
  
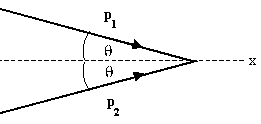
  p_1x + p_2x = p_fx = p_f,  p_1y + p_2y = 0.
  2mv cosθ = 2mv/3, cosθ = (1/3), θ = 70.5^o.
  The angle between their initial directions is 2θ = 141^o.

Problem:

The mass of the blue puck is 20% greater than the mass of the green one.  Before colliding, the pucks approach each other with equal and opposite momenta, and the green puck has an initial speed of 10 m/s.  Find the speed of the pucks after the collision, if half the kinetic energy is lost during the collision.

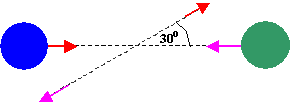
Solution:

• Concepts:
  Inelastic collisions, momentum conservation
• Reasoning:
  The collision is inelastic, since energy is not conserved.
  The total momentum of the two pucks is zero before the collision and after the collision.
  Let particle 1 be the green puck and particle 2 be the blue puck.  Before and after the collision the ratio of the speeds is v₂/v₁ = m₁/m₂ = 1/1.2.
• Details of the calculation:
  The final kinetic energy of the system equals ½ times its initial kinetic energy.
  ½m₁v_1i² + ½m₂v_2i² = 2(½m₁v_1f² + ½m₂v_2f²).
  m₁v_1i² + m₂v_2i² = 2(m₁v_1f²+m₂v_2f²).
  m₁v_1i² + 1.2m₁(v_1i/1.2)² = 2(m₁v_1f² + 1.2m₁(v_1f/1.2)²).
  m₁(v_1i² + v_1i²/1.2) = 2m₁(v_1f² + v_1f²/1.2).
  v_1i² = 2v_1f², v_1f = 0.707v_1i.
  v_1f = 7.07 m/s,  v_2f = 5.89 m/s. 

Problem:

A wooden block of mass M hangs on a massless rope of length L.  A bullet of mass m collides with the block and remains inside the block.  Find the minimum velocity of the bullet so that the block completes a full circle about the point of suspension.

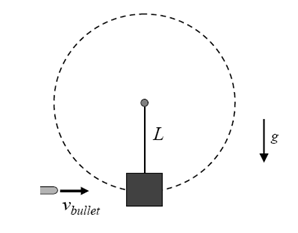
Solution:

• Concepts:
  Inelastic collisions, conservation of momentum, circular motion
• Reasoning:
  Let us treat the block/bullet combination as a point particle.  The block and bullet will start moving in a circle.  The forces on the block/bullet are the force of gravity and the tension in the rope.  If the initial speed is large enough so that the block/bullet gains a height greater than L, then the centripetal acceleration needed to keep the block/bullet moving on the circle is partly provided by gravity and the tension decreases.  When the tension vanishes then the block/bullet behaves like a free particle in a gravitational field executes projectile motion.
• Details of the calculation:
  Conservation of momentum: 
  mv_bullet = (M + m)v,  v = mv_bullet/(M + m)
  When the block/bullet reaches the top of the circle with a speed v_top, so that the centripetal acceleration v_top²/L  > g, then it will completes a full circle about the point of suspension.   
  ½(M + m)v² - 2(M + m)gL = ½(M + m)v_top²
  v_top² = v² - 4gL =  [m/(M + m)]²(v_bullet)² - 4gL.
  We need [m/(M + m)]²(v_bullet)²/L - 4g > g  --> v_bullet  >  (5gL)^½ (M + m)/m.

Problem:

A car of total mass M₁ = M and velocity v₁ makes a totally inelastic collision at time t = 0 with a second car of mass M₂ = 2M at rest.  Before the collision a point object of mass m << M was sitting at the bottom of a frictionless spherical cavity of radius r embodied inside the first car.  For what range of velocities v₁ will the small mass lose contact with the surface of the cavity?

Solution:

• Concepts:
  Inelastic collisions, Newton's laws, conservation of momentum, circular motion, frame transformations
• Reasoning:
  Before the collision car 1 and mass m move with uniform velocity v₁.  The impulse of the collision changes the velocity of car 1, and after the collision car 1 moves with uniform velocity v₂.  The small mass moves with velocity v = v₁ - v₂ with respect to car 1 immediately after the collision.   After the collision the rest frame of car 1 is an inertial frame and we can analyze the problem in that frame.
• Details of the calculation:
  Conservation of momentum:  Mv₁ = 3Mv₂,  v₂ = v₁/3, v = v₁ - v₂ = 2v₁/3.
  In the rest frame of car 1 immediately after the collision we have a particle of mass m at the bottom of a cavity of radius r moving with velocity v.  The particle will start moving in a circle.  The forces on the particle are the force of gravity and the normal force from the wall of the cavity.   If the initial speed is large enough so that the particle gains a height greater than r, then the centripetal acceleration needed to keep the particle moving on the circle is partly provided by gravity and the normal force decreases.  When the normal force vanishes then the particle behaves like a free particle in a gravitational field and looses contact with the wall.

  
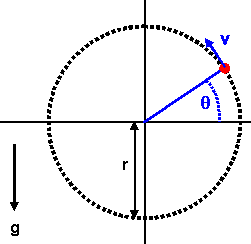
  When ½mv² < mgr,  or  v < (2gr)^½,  or  v₁ < (3/2)(2gr)^½ the particle will not break contact with the wall.
  When the particle reaches the top of the cavity with a speed v_top, so that the centripetal acceleration v_top²/r > g, then it will not break contact with the wall. 
  Then ½mv² = 2mgr + ½mv_top² > 2mgr + ½mgr = (5/2)mgr.
  v > (5gr)^½,  v₁ > (3/2)(5gr)^½.
  For initial velocities (3/2)(2gr)^½ < v₁ < (3/2)(5gr)^½ the particle breaks contact with the wall.

Problem:

A brick is thrown (from ground level) with speed V at an angle θ with respect to the (horizontal) ground.   Assume that the long face of the brick remains parallel to the ground at all times, and that there is no deformation in the ground or the brick when the brick hits the ground.  If the coefficient of friction between the brick and the ground is μ what should θ be so that the brick travels the maximum total horizontal distance before finally coming to rest?

Solution:

• Concepts:
  Projectile motion, impulsive forces
• Reasoning:
  The normal force from the ground has to provide an impulse to reduce the vertical component of the momentum of the brick to zero.
• Details of the calculation:
  Let V be the initial speed.  The horizontal speed and initial vertical speed are then Vcosθ and Vsinθ, respectively.  The horizontal distance traveled in the air is the standard
  d_air = 2V²sinθcosθ/g.
  To find the distance traveled along the ground, we must determine the horizontal speed just after the impact has occurred.  The normal force, N, from the ground is what reduces the vertical speed from V sinθ to zero, during the impact.  So we have
  ∫ N dt = m V sinθ,
  where the integral runs over the time of the impact.  But this normal force (when multiplied by μ to give the horizontal friction force) also produces a sudden decrease in the horizontal speed, during the time of the impact.  So we have 
  m ∆v_x = -∫ μN dt = -μ m Vsinθ,
  which implies ∆v_x = -μ Vsinθ.
  (We have neglected the effect of the mg gravitational force during the short time of the impact, since it is much smaller than the N impulsive force.)   Therefore, the brick begins its sliding motion with speed
  v = Vcosθ - μ Vsinθ.
  (Note that this is true only if tanθ < 1/μ.  If μ is larger than this, then the horizontal speed simply becomes zero, and the brick moves no further.)
  The friction force from this point on is μmg, so the acceleration is a = -μg.  The distance traveled along the ground is
  d_ground = (Vcosθ - μ Vsinθ)²/(2μg).
  We want to find the angle that maximizes the total distance, d_total = d_air + d_ground.
  d(d_total)/dθ = 0.  d(sinθcosθ + cos²θ/(2μ) + μ sin²θ/2)/dθ = 0.
  cos²θ - sin²θ + sinθ cosθ (μ - 1/μ) = 0.  cos(2θ) + sin(2θ)½(μ - 1/μ) = 0.
  tan(2θ) = 2μ/(1 - μ²). 
  Using the trigonometric identity, tan(2θ) = 2 tanθ/(1 - tan²θ) we have tanθ = μ.
  Taking the derivative with respect to θ, we see that the maximum total distance is achieved when tanθ = μ.
  Note, however, that the above analysis is valid only if tanθ < 1/μ.  We therefore see that if μ  < 1, then the optimal angle is given by tanθ = μ.  (The brick continues to slide after the impact.  If μ > 1, then the optimal angle is θ = 45^o.  (The brick stops after the impact, and μ = 45^o gives the maximum value for the d_air.

Problem:

A marble bounces down stairs in a regular manner, hitting each step at the same place and bouncing the same height above each step. 

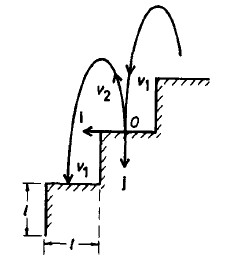
The stair height equals its depth (tread = rise) and the coefficient of restitution ε is given.  Find the necessary horizontal velocity and bounce height.  
(The coefficient of restitution is defined as ε = -v_f/v_i, where v_f and v_i are the vertical velocities just after and before the bounce. respectively).