Kinematics (projectile motion)

Problem:

A cannon ball is shot from ground level towards a target.  Its initial velocity is v₀ = 125 m/s at an angle θ = 37 degrees with the horizontal.  Neglect air resistance.
(a)  What are the horizontal and vertical components of the initial velocity?
(b)  What is the maximum height of the cannonball?  How long does it take to reach this height?
(c)  How long does it take to hit the ground?  When it does so, what is its horizontal distance from its starting point?
(d)  What are its height and its horizontal displacement after it has been in the air for 10 s? 
What is its velocity (magnitude and direction) after it has been in the air for 10 s?

Solution:

• Concepts:
  Kinematic equations, projectile motion
• Reasoning:
  We have motion with constant acceleration.
• Details of the calculation:
  (a)  v₀ = 125 m/s, θ = 37 degrees.
  v_x(0) = v₀cosθ = 99.8 m/s ~100 m/s,  v_y(0) = v₀sinθ  = 75.2 m/s ~ 75 m/s.
  (b)  v_y(t_max-height) = v_y(0) - gt_max-height = 0,  t_maxheight = 7.7 s.
  v_y(t)² = v_y(0)² - 2gy,  v_y(0)² = 2gy_max,  y_max = 287 m.
  (c)  Time to hit ground = 2*7.7s = 15.4 s.  Distance  = v₀cosθ*15.4 s = 1540 m.
  (d)  y(10 s) = 260 m,  x(10 s) = 1000 m.
  v_x(10 s) = 100 m/s,  v_y(10 s) = -23 m/s, v = (v_x² + v_y²)^½ = 102.6 m/s.
  tanθ = v_y/v_x, θ ~ -13^o.

Problem:

Two trucks are parked back to back in opposite directions on a straight, horizontal road.  The trucks quickly accelerate simultaneously to 3.0 m/s in opposite directions and maintain these velocities.  When the backs of the trucks are 20 meters apart, a boy in the back of one truck throws a stone at an angle of 40 degrees above the horizontal at the other truck.  How fast must he throw, relative to the truck, if the stone is to just land in the back of the other truck?

Solution:

• Concepts:
  Kinematic, projectile motion
• Reasoning:
  The stone's motion is motion in two dimensions with constant acceleration.
  Put the origin of the coordinate system at the back of the parked trucks and let the boy be in the truck moving into the negative x direction.  When each truck has moved 10 m, is speed is v = 3 m/s.  Let v be the speed of the stone relative to the truck.
• Details of the calculation:
  The x-component of the stone's speed with respect to the ground is v_x = v cos40^o - 3 m/s.
  The y-component of the stone's speed with respect to the ground is v_y = v sin40^o.
  For the stone is to just land in the back of the other truck we need
  v_xt = 20 m + (3 m/s)t.   0 = v_yt - ½gt²,  t = 2v_y/g.
  Therefore
  2v_xv_y/g = 20 m + (3 m/s) 2v_y/g.
  v_xv_y = g 10 m + (3 m/s) v_y.
  (v cos40^o - 3 m/s) v sin40^o = g 10 m + (3 m/s) v sin40^o.
  v² cos40^o sin40^o = g 10 m + (6 m/s) v sin40^o.
  v² = 199 (m/s)² + 7.83 (m/s) v.
  v = 18.56 m/s.

Problem:

A player tossed a ball at some angle relative to the horizon.  The maximum speed of the ball during the flight was 12 m/sec and the minimum speed was 6 m/sec.  What was the maximum height of the ball during the flight?  Please neglect air resistance.

Solution:

• Concepts:
  Kinematics, projectile motion
• Reasoning:
  The ball executes projectile motion.
• Details of the calculation:
  v_x = v₀cosθ₀ = constant,  x = v₀cosθ₀t,
  v_y = v₀sinθ₀ - gt, y = v₀sinθ₀t - ½gt².
  Since v_x = constant and v_y = 0 when the ball reaches its maximum elevation,
  v_max = v₀ = 12 m/s and v_min = v₀cosθ₀ = 6 m/s.  Therefore cosθ₀ = ½,  θ₀ = 60^o.
  t_{max_height} = v_y0/g = v₀sinθ₀/g.  y_max = ½(v₀sinθ₀)²/g = 5.5 m.

Problem:

A rock is launched from the ground level at a speed v directed at an angle θ with the horizontal.  It is noticed that some (unknown) time t after the launch, the distance between the rock and the launch point begins to decrease.
(a)  Find the smallest launch angle θ consistent with this observation.
(b)  Find t, neglecting the air resistance.

Solution:

• Concepts:
  Kinematics, projectile motion
• Reasoning:
  The rock is a projectile.
  For projectile motion we have x = v cosθ t,  y = v sinθ t - ½gt².
• Details of the calculation:
  (a)  The distance between the rock and the launch point is D = (x² + y²)^½ = (v²t² + g²t⁴/4 - vgt³sinθ)^½.
  For 0 < θ < 90^o and v > 0 the distance D increases initially.  To find extrema for D we set
  dD²/dt =  t(g²t² - 3vgt sinθ + 2v²) = 0.
  t² - 3(v/g) sinθ t + 2v²/g² = 0,  t = [3v/(2g)][sinθ ± (sin²θ - 8/9)^½].
  If sin²θ > 8/9 or θ > 70.5287^o, then two extrema exist.
  The figure below shows a plot of D versus t for v = 10 m/s and a launch angle smaller, equal, or greater than the critical angle θ > 70.5287^o.
  
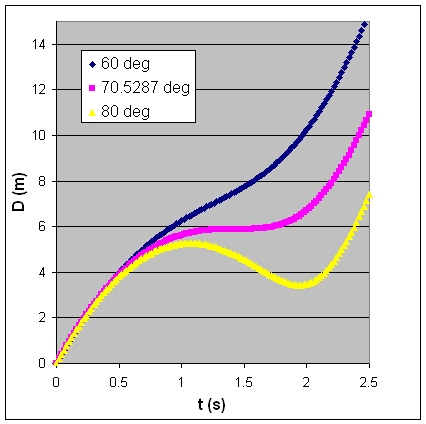
  The smallest launch angle θ consistent with the observation is just greater than 70.5287^o.
  (b)  t = t₁ = [3v/(2g)][sinθ - (sin²θ - 8/9)^½] is the maximum we are looking for.  For t > t₁ D decrease and for
  t > t₂ = [3v/(2g)][sinθ + (sin²θ - 8/9)^½] it increases again.
  The rock hits the ground at t = 2vsinθ/g.

Problem:

Two points, A and B, are located on the ground a certain distance d apart.  Two rocks are launched simultaneously from points A and B, with equal speeds but at different angles.  Each rock lands at the launch point of the other.  Knowing that one of the rocks is launched at an angle θ₀ > 45^o, find the minimum distance between the rocks during the flight in terms of d and θ₀?

Solution:

• Concepts:
  Kinematics, projectile motion
• Reasoning:
  We have to find the position of both rocks as a function of time.
  The range of a projectile launched with speed v₀ at an angle θ₀ with respect to the horizontal x-axis is d = v₀²sin(2θ₀)/g.
  For two projectile launched with the same speed v₀ to have the same range they have to be launched at angles θ_± = π/4 ± θ.
• Details of the calculation:
  Assume rock 1 is thrown from point A with speed v₀ and launch angle
  θ₊ = θ₀ = π/4 + θ towards point B.
  Let the origin of the coordinate system be at point A, let the x-axis point towards B and let the y-axis point upward.
  For rock 1 we have
  x₁(t) = v₀cos(π/4 + θ)t,  y₁(t) = v₀sin(π/4 + θ)t - ½gt².
  Assume rock 2 is thrown from point with speed v₀ and launch angle θ_- = π/4 - θ towards point A. 
  For rock 2 we have
  x₂(t) = d - v₀cos(π/4 - θ)t,  y₂(t) = v₀sin(π/4 - θ)t - ½gt².
  Let the distance between the rocks be L(t).
  L²(t) = (x₂(t) - x₁(t))² + (y₂(t) - y₁(t))²
  = v₀²t²(d/(v₀t) - cos(π/4 - θ) - cos(π/4 + θ))² + v₀²t²(sin(π/4 - θ) - sin(π/4 + θ))²
  = v₀²t²(d/(v₀t) - cos(π/4)cos(θ) - sin(π/4)sin(θ) - cos(π/4)cos(θ) + sin(π/4)sin(θ))²
  + v₀²t²(sin(π/4)cos(θ) - cos(π/4)sin(θ) - sin(π/4)cos(θ) - cos(π/4)sin(θ))²
  = 4v₀²t²(d/(2v₀t) - cos(π/4)cos(θ))² + 4v₀²t²cos²(π/4)sin²(θ)
  = d² + 4v₀²t²cos²(π/4)(cos²(θ) + sin²(θ)) - 4v₀²t²dcos(π/4)cos(θ)/(v₀t)
  = d² + 2v₀²t² - 4v₀tdcos(π/4)cos(θ).
  To find the time at which L²(t) has a minimum, set
  dL²(t)/dt = 4v₀²t - 4v₀dcos(π/4)cos(θ) = 0.
  t_min = dcos(π/4)cos(θ)/v₀.
  L²(t_min) = d² + d²cos²(θ) - 2d²cos²(θ) = d² - d²cos²(θ).
  L_min = dsin(θ) = dsin(θ₀ - π/4) is the minimum distance between the rocks.

Problem:

A catapult set on the ground can launch a rock a maximum horizontal distance L.  What would be the maximum horizontal launch distance if the catapult is set on a platform moving forward with constant speed equal to the launch speed of the rock?
Neglect the air resistance and assume that the rock is launched from the ground level in both cases.

Solution:

• Concepts:
  Kinematic equations, projectile motion
• Reasoning:
  We have motion with constant acceleration.
• Details of the calculation:
  Let θ₀ be the launch angle with respect to the horizontal.  (v_x = v cosθ₀, v_y = v sinθ₀)
  The range of a projectile is R = (v₀²sin2θ₀)/g.
  For the stationary catapult:  R_max = v₀²/g = L,  v₀ = (gL)^1/2.  (θ₀ = 45^o)
  For the moving catapult:  R = (v₀²sin2θ₀)/g  + v₀t. 
  t = 2v_y/g = 2v₀sinθ₀/g.
  R = (v₀²sin2θ₀)/g  + 2v₀²sinθ₀/g,
  dR/dθ₀ = 0 -->  cos2θ₀ = -cosθ_0.  θ₀ = 60⁰.
  R = (v₀²/g)[sin2θ₀  + 2sinθ₀] 
  = L 3√3/2.

Problem:

Consider a lawn sprayer consisting of a spherical cap (α₀ = 45^o) provided with a large number of equal holes through which water is ejected with speed v₀.  The lawn is not evenly sprayed if the holes are evenly spaced.  How must the number of holes per unit area, r(α), be chosen to achieve uniform spraying of a circular area?  Assume the radius of the sprinkler cap is very much less than the radius of the area to be sprayed, and the surface of the cap is at the level of the lawn.

Solution:

• Concepts:
  Kinematics, projectile motion
• Reasoning:
  The drops are projectiles.  They execute motion in more than one dimension motion with constant acceleration.  This acceleration is directed downward and has magnitude g.
  A drop sprayed from an angle a travels a distance R(α).  We want to find this range R in term of α.
  We use
  v_y0 = v₀cosα,  v_x0 = v₀sinα,
  x = x₀ + v_x0t,  y = y₀ + v_y0t - ½gt²,
  and substitute
  0 = 0 + v₀(cosα)t - (½gt²),   t = 2v₀cosα /g
  to solve for
  R = x(t) = v₀(sinα)t  = v₀(sinα)2v₀(cosα)/g = v₀²(sin2α )/g.
• Details of the calculation:
  Drops sprayed from any angles between α and α + dα fall on an area 2πRdR between R and R + dR.
  The number of drops sprayed from angles between α and α + dα is proportional to ρ(α)2πr²_capsin α dα.
  We want
  [ρ(α)2πr²_capsinα dα]/[2πRdR] = const,
  or
  (ρ(α)sinα)/(RdR/dα) = const.
  dR/dα = 2v₀²(cos2α)/g.
  Therefore
  ρ(α )(sinα)/(cos2α sin2α) = const,
  or
  ρ(α ) is proportional to sin(4α) /sinα.

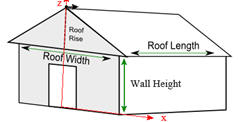
Problem:

A particle is launched with velocity v = 2 ft/s j along the ridge of a roof, but the equilibriums is unstable and it immediately starts accelerating down the right side of the roof.  Using the coordinate
system in the figure and neglecting friction, what are the particle's x- and y-coordinates when it hits the ground?
Use the following measurements:  |
Roof Rise: z_R = 4 ft; Roof Width: x_R= 24 ft;  Roof Length: y_R = 24 ft; 
Wall Height: z_W = 8 ft;  g = 32 ft/s².

Solution:
 

• Concepts:
  Kinematics, motion with piecewise constant acceleration, energy conservation
• Reasoning:
  The forces acting on the particle are gravity and the normal force of the roof.  The motion in the xz plane is independent of the motion with constant v_y in the y-direction.
• Details of the calculation:
  Consider only the motion in the xz plane:  mg∆h = ½mv².  (v² = v_x² + v_y²)
  As long as the particle is in contact the roof:  a = gsinθ.  sinθ = 4/(160)^½ = 0.316.
  For the motion to the edge of the roof:  v₁ = (2g z_R)^½ = 16 ft/s   v₁ = gsinθ t₁,  t₁ = 1.58 s.
  
  [Check that the particle stays on the roof during the time interval t₁.
  During time t₁, the particle travels a distance d = 2 ft/s *t₁ = 3.16 ft in the y direction, which is less than y_R.  The particle stays on the roof.  At the edge of the roof the particle's velocity is
  v = g sinθ cosθ t₁ i - g sinθ sinθ t₁ k + 2 ft/s j. =15.18 ft/s i - 5.06 ft/s k + 2 ft/s j.]
  
  The particle contacts the floor after an additional time t².  8ft - v_1zt₂ - ½gt₂² = 0  t₂ = 0.568 s.
  The particle's x and y coordinates at time t₂ are x = 12 ft + g sinθ cosθ t₁ t₂ = 20.62 ft,
  y = 3.16 ft + 2 ft/s (t₂ - t₁) = 4.3 ft.

Problem:

In a carnival game, you have to throw a ball with speed v₀ at an angle θ in order to hit a target on the other side of the platform, located a distance h away.  The platform is inclined at an angle φ.  Find the angle θ in terms of the other variables.  

Solution:

• Concepts:
  Kinematics, projectile motion
• Reasoning:
  Orient the x and y axes of your coordinate system as shown.
  
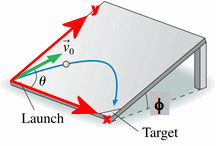
  The net force acting on the ball in a direction perpendicular
  to the xy-plane is zero.
  In the x-y plane a_x = 0, a_y = -gsinφ = -g'. 
• Details of the calculation:
  The range of the ball is h = (v₀²sin2θ)/g'.
  sin2θ = h gsinφ/v₀²,  θ = ½ sin^-1(h gsinφ/v₀²).

Problem:

A tree trunk lies on the ground.  The trunk has a shape of a cylinder with radius R.  A flea attempts to jump over the trunk.  What is the minimum initial speed v that enables the flea to reach the other side?  Assume that the flea is intelligent enough to select the optimal take-off point on the ground.
Consider two cases.
(a)  The flea is allowed to slide on the frictionless trunk.
(b)  The flea is not allowed to slide on the trunk and must clear the trunk.

Solution:

• Concepts:
  Kinematics, projectile motion
• Reasoning:
  (a)  Imagine the flea sitting on top of the trunk.  This is an unstable equilibrium and the slightest perturbation will cause it to slide off.  Its kinetic energy when reaching the ground will be
  ½mv² = 2mgR.  The motion may be reversed.
  (b) The flea's trajectory must be a parabola as shown.
  
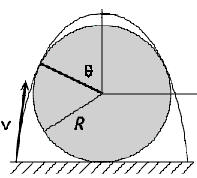
• Details of the calculation:
  (a)  The flea must jump with a speed greater than v = 2(gR)^½.
  (b)  Let the parabolic arc of the flea be tangent to the trunk at an angle θ from the top of the trunk.
  The velocity of the flea at this point is v_θ = (v_θcosθ, v_θsinθ). 
  The conditions for the parabola to reach its maximum over the center of trunk are
  v_θcosθ t = r sinθ, v_θsinθ = gt  for some t.  (v_θy must be zero at the top.)
  These give v_θ² = rg/cosθ.
  Let v be the speed with which the flea jumps from the ground. Then the energy at the ground is
  ½ mv² = mg(r + r cosθ) + ½mrg/cosθ = mgr(1 + cosθ + 1/(2cosθ)).
  Minimizing this function of cosθ yields cosθ = 1/√2, θ = 45^o.
  The minimum initial speed is v² = 2gr(1 + √2),  v = 2.197 (gr)^½.

Problem:

A marble bounces down stairs in a regular manner, hitting each step at the same place and bouncing the same height above each step. 

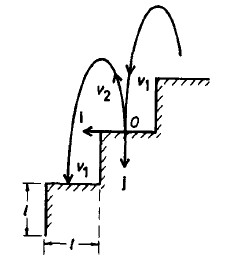
The stair height equals its depth (tread = rise) and the coefficient of restitution ε is given.  Find the necessary horizontal velocity and bounce height.  
(The coefficient of restitution is defined as ε = -v_f/v_i, where v_f and v_i are the vertical velocities just after and before the bounce. respectively).

Solution:

• Concepts:
  Kinematics, collisions, motion with constant acceleration
• Reasoning:
  The horizontal component of the velocity of the marble, v_h, is constant.  Let v_i and v_f denote the magnitudes of the vertical components of the velocity of the marble just before and just after a bounce, respectively.  Since the conditions at each step are exactly the same, v_i and v_f are also constants.  The relationship between the magnitudes of v₁ = v_hi - v_ij and v₂ = v_hi + v_fj is found from the conservation of mechanical energy in a conservative field.  ½mv₂² + mgl = ½mv₁².
• Details of the calculation:
  v₂² + 2gl = v₁².  v_i² - 2gl = v_f² = ε²v_i².  v_i² = 2gl/(1 - ε²).
  What is the time between bounces?
  Starting with a vertical velocity v_f, the time to reach the point where the vertical velocity is zero is t₁ = v_f/g. 
  The time to accelerate downward from this point and reach a vertical velocity -v_i is t₂ = |v_i|/g.
  The total time between bounces is t = t₁ + t₂ = (v_f + |v_i|)/g = l/v_h, since during this time the marble has to cover a horizontal distance l.
  v_h = gl/(v_f + |v_i|) = gl/[(1 + ε)|v_i|] = (gl/2)^½[(1 - ε)/(1 + ε)]^½.
  The bounce height h is found from conservation of energy.  ½mv_f² = mgh, h = v_f²/(2g) = ε²l/(1 - ε²).

Problem:

(a)  An astronaut on a strange planet finds that she can jump a maximum horizontal distance of 15 m if her initial speed is 3 m/s.  What is the free-fall acceleration on the planet?
(b)  How much work is required to raise a 100 g block to a height of 200 cm and simultaneously give it a velocity of 300 cm/sec?

Problem:

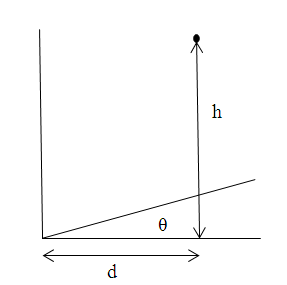
An plane, inclined at θ = 20^o, touches a wall as shown in the picture.  You drop a small, perfectly elastic ball from a height h = 1.5 m onto the onto the plane.  The ball falls from rest.  You do not move your hand.  At what distance d from the wall do you have to drop it so that it bounces back into your hand?

Problem:

A wheel of radius b is rolling along a muddy road with a speed v.  Particles of mud attached to the wheel are being continuously thrown off from all points of the wheel.  If v² > 2bg, where g is the acceleration of gravity, find the maximum height above the road attained by the mud, H = H(b,v,g).