Work

Problem:

(a)  An astronaut on a strange planet finds that she can jump a maximum horizontal distance of 15 m if her initial speed is 3 m/s.  What is the free-fall acceleration on the planet?
(b)  How much work is required to raise a 100 g block to a height of 200 cm and simultaneously give it a velocity of 300 cm/sec?

Solution:

• Concepts:
  (a) Projectile motion,  (b) Energy and work
• Reasoning:
  (a) After she has left the ground, the astronaut becomes a projectile.  (Her motion is motion in more than one dimension with constant acceleration.)  The maximum range of a projectile is associated with a launch angle of 45^o.
  (b) To change the total energy of an object, an external force must do work.
• Details of the calculation:
  (a)  range: R = v₀²sin2θ₀/g',  R_max = v₀²/g',  g' = (9/15)(m/s²) = 0.6 m/s².
  (b)  W = mgh + ½mv² = 0.1*9.8*2 J + 0.5*0.1*9 J = 2.41 J.

Problem:

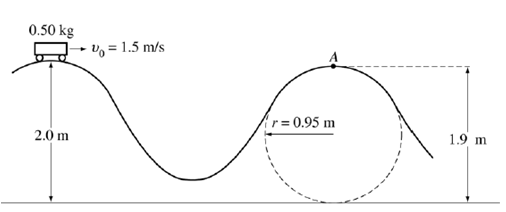
A designer is working on a new roller coaster, and she begins by making a scale model.  In this model, a car of total mass m = 0.5 kg moves with negligible friction along the track shown.  The car is given an initial speed v₀ = 1/5 m/s at the top of the first hill of height 2 m.  Point A is located at a height of 1.9 m at the top of the second hill, the upper part of which is a circular arc of radius 0.95 m.

(a)  Calculate the speed of the car at point A.
(b)  Calculate the magnitude of the force of the track on the car at point A.
(c)  In order to stop the car at point A, some friction must be introduced.  Calculate the work that must be done by the frictional force in order to stop the car at point A.

Solution:

• Concepts:
  Energy conservation, centripetal force
• Reasoning:
  The gravitational force is a conservative force.
• Details of the calculation:
  (a)  Energy conservation
  ½mv₀² + mgh₀ = ½mv_A² + mgh_A
  v_A² = v₀² + 2g(h₀ - h_A)
  v_A² = (1.5 m/s)² + 2(9.8 m/s²)(2 m - 1.9 m) = 4.21 (m/s)²
  v_A = 2.05 m/s
  (b)  The net force is equal to the centripetal force.
  F_net = mg - N = mv_A²/r,  N = mg - mv_A²/r = (0.5 kg)(9.8 m/s²) - (0.5 kg)(4.21 m²/s²)/(0.95 m) = 2.7 N
  (c)  The work done must be equal to the kinetic energy at point A in the absence of friction.
  W_friction = -½mv_A² = -½(0.5 kg)(4.21 m²/s²) = -1.05 J

Problem:

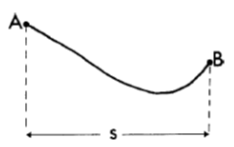
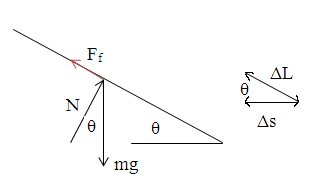
A skier starts from rest at point A and slides down the hill, without turning or braking.  The coefficient of friction is μ.  When he stops at point B his horizontal displacement is s.  What is the height difference between points A and B?

Solution:

• Concepts:
  Work and energy
• Reasoning:
  The work done by the force of friction equals the change in gravitational potential energy.
• Details of the calculation:
  The magnitude of the frictional force is F_f = μmgcosθ = μmg∆s/∆L.
  
  ∆W_f  = -F_f∆L = μmg∆s,  W_f = -μmgs.  mgh_A - mgh_B = mg∆h = μmgs.  ∆h = μs. 

Problem:

A free particle with mass m is subjected to a time-dependent force F(t) = F₀ exp(-t/τ) for t > 0.  F₀ and τ are constants.
(a)  Find the velocity v(t) of the particle as a function of time, given that v = 0 at time t = 0.
(b)  What is the total work done on the particle by the force as t --> infinity?