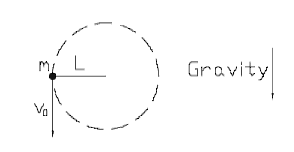Circular motion, centripetal acceleration, in a uniform gravitational field

Problem :

Find the minimum rotational frequency (i.e. the number of rotations per second, not the angular frequency) required to rotate a bucket containing 4 liters of water in a circular path in a vertical plane at an arm's length (about 70 cm) without spilling water.

Solution:

• Concepts:
  Centripetal acceleration
• Reasoning:
  Assume constant ω.  Then on top of the circular path the centripetal acceleration needed to keep the water moving in a circle must be greater than or equal to the gravitational acceleration g.
  Limiting case:  v²/R = g,  v = (gR)^½.
• Details of the calculation:
  f = v/(2πR) = (g/R)^½/(2π) = ((9.8 m/s²)/(0.7 m))^½/(2π) = 0.6/s.

Problem:

A small mass slides without friction down the loop track shown in the figure below.
(a)  Show that the speed at point B must be at least as large as (gR)^½ if the mass does not fall away from the track.
(b) What must be the height h required to achieve the speed found in (a)?  Give your answers in terms of R.

Solution:

• Concepts:
  Centripetal acceleration, energy conservation
• Reasoning:
  We need to make sure that the normal force does not vanish at any position on the upper half of the track except possibly on the top, at θ = 90^o.  The normal force must be partly responsible for the centripetal acceleration v²/R, otherwise we have projectile motion.
• Details of the calculation:
  (a)  On the upper half of the track, the centripetal acceleration needed to keep the mass moving on the circle is partly provided by gravity and partly by the normal force.  When the normal force vanishes, then the mass behaves like a free particle in a gravitational field.  We need to make sure that the normal force does not vanish at any position on the upper half of the track except possibly on the top, at θ = 90^o.
  mv²/R = mgsinθ + N.  We need N > 0, therefore we need v²/R > gsinθ for all θ not equal to 90^o.  We need v ≥ (gR)^½.
  (b)  Energy conservation:  mgh = mg2R + ½mv², with v² = gR.
  h = 2R + ½ R = 2.5 R.

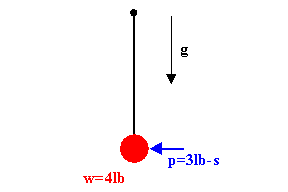
Problem:

A ball is weighing 4 pounds is suspended by a weightless string of length 6 ft.  The ball is delivered a horizontal impulse of magnitude 3 pounds-seconds.  Find the maximum height above its initial position, attained by the ball.  Take 32 ft/s² as the gravitational acceleration and assume there is no friction at the point of attachment of the string.

Solution:

• Concepts:
  Circular motion, energy conservation
• Reasoning:
  We treat the ball as a point particle.  (Not enough information is given to treat it as a rigid body.)  Initially the ball receives an impulse of magnitude FΔt = p₀.  It's kinetic energy is now p₀²/2m.   It will start moving in a circle.  The forces on the ball are the force of gravity and the tension in the string.   If the initial impulse is large enough so that the ball rises above the pivot point, then the centripetal acceleration needed to keep the ball moving on the circle is partly provided by gravity and the tension in the string decreases.  When the tension in the string vanishes then the ball behaves like a free particle in a gravitational field.
  Refer to the figure below:
  
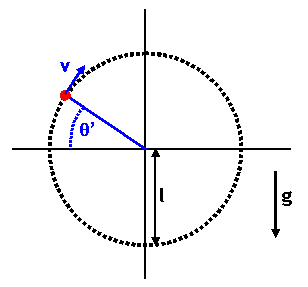
  Energy conservation:  E = ½p₀²/(2m) = ½mv² + mg (l + l sinθ'),
  v²/l = 2E/(ml) - 2g(1 + sinθ') is the centripetal acceleration.
  The tension in the string vanishes when v²/l = g sinθ', i.e. when all the centripetal acceleration is due to gravity.  Then
  sinθ' = 2E/(3mgl) - (2/3).
• Details of the calculation:
  E = p₀²/(2m) = (9 lb²s² 32 ft)/(8 lbs²) = 36 lb ft, since m =  4 lbs²/(32 ft) .
  l = 6 ft.
  Therefore sinθ' = (1/3), θ' = 19.47^o.
  At θ' = 19.47^o we have v = (lg sinθ')^½, v_x = v sinθ', v_y = v cosθ'.
  The ball now behaves like a projectile.  It will gain an additional height Δh.
  ½mv_y² = mgΔh, Δh = (l sinθ' cos²θ')/2.
  Δh = 3 ft*0.296 = 0.89 ft
  Maximum height:
  l + l sinθ' + Δh = 6 ft + 2 ft + 0.89 ft = 8.89 ft

Problem

A child slides down a frictionless slide as shown in figure.
(a) What is the minimum value of R for the child to not immediately loose contact with the section of radius R?
(b) If R is larger than that minimum value at what height h will the child loose contact with the section of radius R?

(c)  If R is smaller than that minimum value, how far from the end of the section with radius R will the child land?

Solution:

• Concepts:
  Centripetal acceleration, energy conservation
• Reasoning:
  Energy conservation yields the speed of the child when it reaches the top of the section with radius R.  The centripetal acceleration needed to move in a circular path of radius R is v²/R.  If g > v²/R then gravity can provide the centripetal acceleration.
• Details of the calculation:
  (a)  When the child reaches the top of the section with radius R it has kinetic energy ½mv² = mg(H - R), and it is moving in the positive x-direction.  If g > v²/R then gravity can provide the centripetal acceleration.
  We need 1 > 2(H - R)/R, R > (2/3)H for the child to stay in contact with the section with radius R.
  (b) The child's velocity as a function of h is given by v = (2g(H - h))^½.  As long as the gh/R > 2g(H - h)/R, gravity can provide the centripetal acceleration needed for the child to move in a circular path.  (gh/R is the radial component of g.)  When h = 2H/3, the child will loose contact with the circular section.
  (c)  If R < (2/3)H:  x + R = (2g(H-R))^½t,  t = (2R/g)^½, x = 2(R(H - R))^½ - R.  The child will land a distance x = 2(R(H - R))^½ - R from the end of the section with radius R.

Problem:

A massless string of length L has a ball of mass m attached to one end and the other end is fixed.  The ball is launched so that it moves in a vertical circle in a gravitational field, with an initial velocity v₀ downward.  What is the minimum value for v₀ if the ball is to rotate around on a circle of radius L?

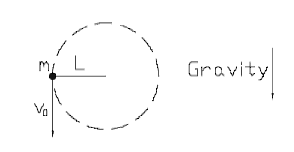
Solution:

• Concepts:
  Energy conservation, centripetal acceleration
• Reasoning:
  Place the origin of the coordinate system at the center of the circle and let the y-axis point upwards.  For y > 0 the centripetal acceleration needed to keep the ball moving on the circle is partly provided by gravity and the tension in the string decreases.  When the tension in the string vanishes then the ball behaves like a free particle in a gravitational field.  The minimum value for v₀ is the one for which the tension vanishes when the ball is on the top of the circle.
• Details of the calculation:
  Energy conservation: E = ½mv₀² = ½mv² + mg Lsinφ.
  Here φ is the usual polar angle.
  v²/L = v₀²/L - 2gsinφ is the centripetal acceleration.
  The tension in the string vanishes when v²/L = gsinφ, when all the centripetal acceleration is due to gravity.
  For the ball is to rotate around on a circle of radius L we need v²/L ≥ g when φ = 90^o.
  We need v₀²/L ≥ 3g,  v₀ ≥ (3gL)^½.
  The minimum value of v₀ is (3gL)^½.

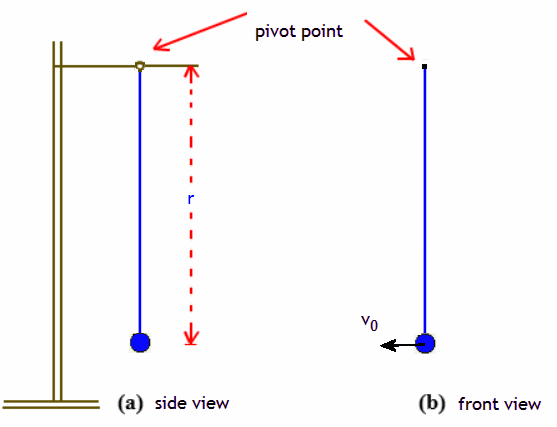
Problem:

A particle attached to the end of a light (massless) string of length r suspended from a very thin rod.  Initially the particle is at rest.  It is given an horizontal impulse which results in an horizontal velocity v₀ right after the impulse.  What is the minimum speed v₀ that allows the string to wrap around the pivot rod at least once?

Solution:

• Concepts:
  Circular motion, projectile motion
• Reasoning:
  Initially the particle has kinetic energy ½mv₀².  It starts moving in a circle.  The forces on the particle are the force of gravity and the tension in the string.   If the initial kinetic energy is large enough so that the particle rises above the pivot point, then the centripetal acceleration needed to keep the ball moving on the circle is partly provided by gravity and the tension in the string decreases.  When the tension in the string vanishes then the particle behaves like a free particle in a gravitational field.  It follows a parabolic trajectory.
  
  
  Energy conservation:  E = ½mv₀² = ½mv² + mg (r + r sinθ').
  The tension in the string vanishes when v²/r = g sinθ', i.e. when all the centripetal acceleration is due to gravity. 
• Details of the calculation:
  When the tension vanishes at an angle θ' = θ, we want the parabolic trajectory of the particle to cross the x-axis at x > 0.
  We want -r sinθ = v cosθ t - ½gt²,  r cosθ ≤ v sinθ t. 
  To find the minimum v we use r cosθ = v sinθ t.
  We have three equations for three unknowns.
  t = (r cosθ)/(v sinθ), 
  -sinθ = cos²θ/sinθ - ½gr cos²θ/(v² sin²θ) = cos²θ/sinθ - ½cos²θ/sin³θ.
  cos²θ sin²θ  + sin⁴θ - ½cos²θ = 0.
  sin²θ  - ½cos²θ = 0.  tan²θ = ½.  θ = 35.26^o.
  From energy conservation we have v₀² = v² + 2gr(1 +  sinθ) = gr(3 sinθ + 2).
  The minimum speed v₀ is (gr(3 sinθ + 2))^1/2.

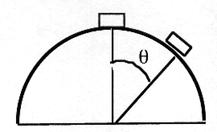
Problem:

A block of mass m starts from rest at θ = 0 and slides without friction under the force of gravity on an inverted hemispherical surface of radius R.  Find the angle θ when the block leaves the surface.

Solution:

• Concepts:
  Newton's 2^nd law, Energy conservation
• Reasoning:
  As long as the block is in contact with the hemisphere we have
  mg + N = ma.  The block looses contact when N = 0. 
• Details of the calculation:
  Radial component:  mgcosθ - N = mv²/R.
  When N = 0, gcosθ = v²/R.
  Energy conservation: ½mv² = mgR(1 - cosθ).
  v²/R = 2g(1 - cosθ).
  Therefore gcosθ = 2g(1 - cosθ), or cosθ = (2/3), θ = 48.2^o when the block looses contact.

Problem

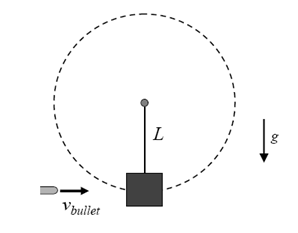
A wooden block of mass M hangs on a massless rope of length L.  A bullet of mass m collides with the block and remains inside the block.  Find the minimum velocity of the bullet so that the block completes a full circle about the point of suspension.

Problem:

A car of total mass M₁ = M and velocity v₁ makes a totally inelastic collision at time t = 0 with a second car of mass M₂ = 2M at rest.  Before the collision a point object of mass m << M was sitting at the bottom of a frictionless spherical cavity of radius r embodied inside the first car.  For what range of velocities v₁ will the small mass lose contact with the surface of the cavity