Kinematics (1D) and describing
trajectories
Describing trajectories
Problem:
A
circle of radius a rolls on a straight line in the positive x-direction. The
trajectory y(x) of a given point P on this circle is a cycloid.
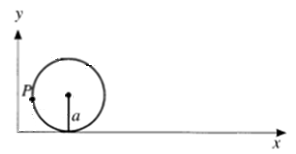
(a) Find the parametric representation x(y) of this cycloid.
(b) Find the length of the path of the point P, when the circle has completed
one revolution, i.e. when the center of the circle has traveled a distance 2πa.
Solution:
- Concepts:
Describing trajectories
- Reasoning:
We are asked for the the parametric representation of the trajectore of a
piont on a rolling circle.
- Details of the calculation:
(a) Let X be the x-coordinate of the center of the circle and x and y the
coordinates of the point P.

X = aθ, x = X -
a sinθ = a θ - a sinθ,
y = a - a cosθ.
θ = cos-1((a - y)/a),
sinθ = (1 - cos2θ)½
= ((2ay - y2)/a2)½.
x = a cos-1((a - y)/a) - (2ay - y2)½.
(b) Let s denote the length of the path.
ds/dθ = [(dx/dθ)2
+ (dy/dθ)2]½.
(dx/dθ)2 = a2(1
- cosθ)2 = a2(1
+ cos2θ - 2cosθ),
(dy/dθ)2 = a2sin2θ.
ds = a(2 - 2cosθ)½dθ.
cos2x = cos2x - sin2x = 1 - 2sin2x
, 1 - cosθ = 2sin2(θ/2)
s = ∫02π
(a√2)(1 - cosθ)½dθ
= ∫02π
(2a) sin(θ/2)dθ
= (4a) ∫0π sinx dx = 8a.
The length of the path is 8a.
Kinematics (1D)
Problem:
A chipmunk is taking a sunbath 5.0 m away from its burrow. It
then decides to go jogging. The chipmunk takes off and runs directly
away from the burrow, so that its velocity is inversely proportional
to the distance from the burrow. If the initial speed of the
chipmunk is 2.0 m/s, how long would it take it to run 15.0 m?
Solution:
- Concepts
Kinematics
- Reasoning:
The chipmunk moves along a straight line. We are given dx/dt = f(x). dt =
dx/f(x). Integrate to find ∆t.
- Details of the calculations
The chipmunk's velocity is v = a/(x + 5), with x measured in meters.
v(x = 0) = 2 m/s, so a = 10 m2/s.
dx/dt = a/(x + 5), (1/a)(x + 5)dx = dt, (1/a)∫015(x
+ 5)dx = ∆t.
∆t = (1/10)(225/2 + 75) s = 18.75 s
Problem:
Laurel running at 10 m/s is 40 m behind Hardy when Hardy
starts from rest on his moped with an acceleration 1.0 m/s2. How
long does it take for Laurel to catch up with Hardy?
Solution:
- Concepts:
Kinematics
- Reasoning:
One person is moving with constant speed and the other with constant
acceleration.
- Details of the calculation:
For Hardy: x = ½at2 = (0.5 m/s2)t2.
For Laurel: x = -40 m + vt = -40 m + (10 m/s)t.
Laurel catches up when (0.5 m/s2)t2 = -40 m + (10 m/s)t.
t2 - 20t + 80 = 0, t = (10 - √20)
s = 5.53 s
At t = (10 + √20) s = 14.47 s Hardy catches up with Laurel.
Problem:
You are traveling east at 30 miles per hour. You see a ball rolling onto the
road and you break hard, because you are afraid that a child will come running
after the ball. You come to a stop in 0.8 seconds. What is the direction of
your average velocity in this short time interval? What is your average
acceleration?
Solution:
- Concepts:
Kinematics
- Reasoning:
Average acceleration: a
= ∆v/∆t
- Details of the calculation:
The
direction of your average velocity is east. You are traveling east with
decreasing speed until you come to a stop.
The change in your velocity is ∆v
= v2 - v1 = 0 - 30
mph east = -30 mph east = 30 mph west. Let us convert to SI units.
30 mph * 1609 m/mile *s 1 h/(3600 s) = 13.4 m/s.
Your average acceleration is ∆v/∆t = (13.4 m/s)/(0.8 s) west = 16.8
m/s2 west.
Problem:
A mass m starting from rest slides without friction in the field of gravity
from the top of a vertical diameter d of a circle, A, along a straight wire
connecting A and a point on the circumference, B. The wire makes an angle θ
with the diameter, as shown in the figure. Does the time it takes to slide from
A to B depend on θ? Justify your answer.
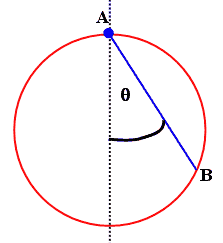
Solution:
- Concepts:
Kinematics
- Reasoning:
We are asked for the time it takes for an object to travel a given distance
when it starts from rest and the acceleration is constant.
The distance x the mass m travels is found from x/2 = (d/2)cosθ.
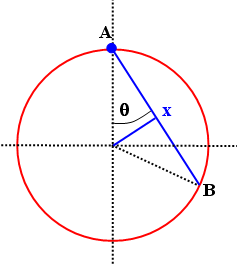
The acceleration of the mass is ax = g cosθ.
Kinematics: x = ½axt2.
- Details of the calculation:
The time t it takes for the mass to reach point B is
t = (2x/ax)½
= (2dcosθ/(gcosθ))½ = (2d/g)½, independent of θ.
Problem:
Two cars approach an intersection of two perpendicular roads as
shown. The velocities of the cars are v1 and v2.
At the moment when car 1 reaches the intersection, the separation
between the cars is d.
What is the minimum separation between the
cars during this motion?
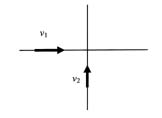
Solution:
- Concepts:
Kinematics
- Reasoning:
Both cars move with constant velocity.
- Details of the calculation:
Let t = 0 denote the time car 1 arrives
at the intersection.
Then for the position of car 1 as a function of time
we have x1(t) = v1t, y1 = 0.
For car 2
we have x2 = 0, y2(t) = d + v2t = d + (v2/v1)x1.
In the problem it is not specified if d is positive or negative.
The
separation between the cars is s = (x12 + y22)½.
s2 = (1 + (v2/v1)2)x12
+ d2 + 2d(v2/v1)x1.
ds2/dx1 = 2(1 + (v2/v1))x1
+ 2d(v2/v1) = 0 --> x1 = -d(v2/v1)
/(1 + (v2/v1)2),
smin2
= (1 + (v2/v1)2)x12 +
d2 + 2d(v2/v1)x1 = d2/(1
+ (v2/v1)2). smin = |d|/(1 + (v2/v1)2)½.
Problem:
A prankster drops a water-filled balloon out of a window. The balloon is
released from rest at a height of 10 m above the ears of an innocent man who is
the target. Then, because of a guilty conscience, the prankster shouts a
warning after the balloon is released. The warning will do no good, however, if
shouted after the balloon reaches a certain point, even if the man could react
infinitely quickly. Ignoring the effect of air resistance on the balloon,
determine how far above the innocent man's ears this point is. The speed of
sound is 340 m/s.
Solution:
- Concepts:
Kinematics
- Reasoning:
The sound has to reach the man before the balloon does.
- Details of the calculation:
It takes sound ts = (10/340) s to travel 10 m.
The balloon reaches the man in tb = (2*10/9.8)½ s = 1.43
s.
If the warning is shouted later than a time tb - ts = 1.4
s after the balloon is dropped, the warning will reach the man after he is hit
by the balloon. In time tb - ts the balloon has dropped a
distance d = ½g (tb - ts)2 = 9.6 m and is
therefore a distance 40 cm above the man.
Problem:
A boy wants to throw a can straight up and then hits it with a second can.
He wants the collision to occur 4 m above the throwing point. In addition, he
knows that the time he needs between throws is 3.0 second. Assuming that he
throws the second can 3.0 seconds after he throws the first can and that he
throws both cans with the same speed, what must the initial speed be? What are
the speeds of both cans when they collide?
Solution:
- Concepts:
Kinematics, energy conservation
- Reasoning:
The only force acting on a can after it leaves the boy's hand is gravity. The
gravitational force is a conservative force.
- Details of the calculation:
Energy conservation requires that the cans have the same speed when they
collide.
The first can must be coming down, and the second can must be going up.
- (v0 - gt) = v0 - g(t - 3s), t = v0/g + 1.5
s.
The cans collide after t = v0/g + 1.5 s.
Their speed when they collide is v = -v0 + gt = g(1.5 s) = 14.7 m/s.
If the collision occurs at a height of 4 m we need
½mv02 = ½mv2 + mg(4 m), v02
= v2 + g(8 m) = 294.49 m2/s2, v0 =
17.16 m/s.
Problem:
A ball that is thrown upward near the surface of the earth with a velocity of
50 m/s will come to rest about 5 second later. If the ball were thrown up
with the same initial velocity on Planet X, after 5 seconds it would still be
moving upwards at nearly 31 m/s. The magnitude of the gravitational field
near the surface of Planet X is what fraction of the gravitational field near
the surface of the earth?
Solution:
- Concepts:
One-dimensional motion with constant acceleration
- Reasoning:
We are given the velocity at t = 0 and t = 5 s and are
asked to find the acceleration.
- Details of the calculation:
v(t) = v0 + at = v0
- g't. 31 m/s = 5 0 m/s - g'(5 s).
g' = 3.8 m/s2. g'/g =
0.388.
Problem:
A projectile launched from the ground explodes into three fragments of equal
mass at the top point of the trajectory. One of the fragments lands t
seconds after the explosion; two other fragments land simultaneously 2t seconds
after the explosion. How high above the ground does the projectile
explode?
Solution:
- Concepts:
Momentum conservation, kinematics
- Reasoning:
Let h be the height above the ground at which the
projectile explodes and vjy (j = 1, 2, 3) the y-component of the
velocity at the moment of the explosion for the three fragments. Label with
1 the fragment which lands after t seconds.
Since the landing time
depends only on the y-component of the velocity at the moment of the
explosion, we have v3y = v2y .
We then need only
the equations for fragments 1 and 2, stating that at the landing time the
y-coordinate will be zero.
h + v1yt - ½gt2 = 0, h
+ 2v2yt - 2gt2 = 0.
- Details of the calculation:
Since the masses of the three fragments
are equal, and the y-component of the projectile momentum at the moment of
the explosion is equal to 0, momentum conservation requires
v1y
+ v2y + v3y = v1y + 2v2y =
0, v2y = -½v1y.
We have 3 equations for 3
unknowns, v1y, v2y, and h.
h + v1yt - ½
gt2 = 0, h - v1yt - 2gt2 = 0.
v1yt
- ½ gt2 = -v1yt - 2gt2, v1y =
-¾gt.
h = ¾gt2 + ½gt2 = (5/4)gt2.
Problem:
A string with 10 beads (bead #0 to #9) attached to it at equal intervals d0
is dropped from a vertical height h. (Bead #0 is at height h when the string is
released.) The sound of each bead is heard when it hits the ground.
(a) Find tn, the time the nth bead hits the ground and evaluate tn/t0.
Does the time interval between sounds increase or decrease a the beads hit the
ground?
(b) Assume we want equally spaced sounds. If the spacing between bead 0 and
bead 1 is d0, what should be the spacing dn between bead n
and bead n + 1?
Solution:
- Concepts:
Kinematics
- Reasoning:
All beads have the same acceleration g, downward. The beads in the upper parts
of the chain accelerate for a longer time before hitting the ground and
therefore have higher speeds when hitting the ground. Each successive bead
moves faster through the last distance d0, and we therefore expect
the time interval between sounds to decrease. If we want equal time intervals
between sounds, the distance between the beads has to increase with height.
- Details of the calculation:
(a)
When the chain is released, the lowest bead (#0) is at height h
and the highest bead (#9) is at height h + 9*d.
The time it takes an object to fall a distance y is t = (2gy)½
(from y = ½gt2).
So tn = (2g)½(h + nd0)½ (n = 0
through 9) is the time when the nth bead hits the ground.
tn = (2gh)½(1 + nd0/h)½, tn/t0
= (1 + nd0/h)½.
tn increases proportional to the square root of n, not linearly with
n, which would be required for equally spaced sounds. The spacing between
sounds decreases.
(b) If we want equally spaced
sounds we need a variable spacing between beads.
We want tn = t0(1 + yn/h)½ = t0
+ nT, where T is the time interval we choose.
We need 1 + yn/h = (1 + nT/t0)2, yn = h 2n T/t0 + h
n2T2/t02.
The spacing between bead n + 1 and bead n is dn = yn+1 - yn
= n2hT2/t02 + hT2/t02 + h2T/t0.
The spacing between bead 0 and bead 1 is hT2/t02+ 2hT/t0 = d0, therefore dn = d0
+ n 2hT2/t02, and T/t0 = 1 + (1 + d0/h)½.
The spacing between the beads
increases linearly with n.
Problem:
Two ferries leave from opposite sides of a river. They
move with different speeds and meet 400 m from the left bank. Each continues to
its destination, take 5 minutes to unload and load, and then starts the return
trip. The ferries meet again 200 m from the right bank. How wide is the river?
Solution:
- Concepts:
Kinematics
- Reasoning:
Kinematics gives us two expression for the ratio vB/vA,
one for the initial and one for the return trip. Setting these equal
to each other allows us to solve for the width W of the river.
- Details of the calculation:
Let ferry B start from the left bank and ferry A start from the right
bank.
vBt1 = W - 400 m, vAt1 = 400 m
vB(t2 - 5 min) = 2W - 200 m, vB(t2
- 5 min) = W + 200 m
vB/vA = (2W - 200 m)/(W + 200 m) = (W - 400 m)/(400 m)
Solve for W: W2 - (1000 m)W = 0, W = 1000 m
Frame transformations
Problem:
A student in a boat wants to cross the river from point K to point L (see the
diagram). The current of the river is v = 2.0 km/h; the speed of the boat in
still water is u = 5.0 km/h. The river is a = 0.25 km wide; distance LM is b =
0.5 km (see the diagram). How long would the trip take?
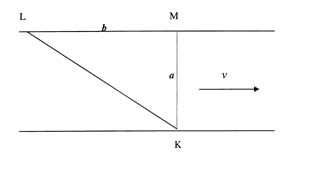
Solution:
- Concepts:
Kinematics, frame transformations
- Reasoning:
In the rest frame of the water, the student has to travel a distance b + vΔt
into the -x direction and a distance a in the y direction in time Δt to move
on a straight line path and to arrive in the minimum time.
We have: -vxΔt = b + vΔt, vyΔt = a, vx2
+ vy2 = u2.
- Details of the calculation:
These are 3 equations for 3 unknowns. Solve for Δt.
vy = a/Δt. vx2 = u2 - a2/Δt2.
vx2Δt2 = b2 + v2Δt2
+ 2bvΔt. (u2 - v2)Δt2 - 2bvΔt - (a2
+ b2) = 0.
21Δt2 - 2Δt - 0.3125 = 0, with Δt in hours. Δt = 0.17858 h.
Problem:
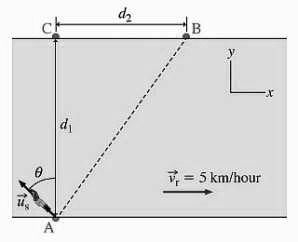 A swimmer wants to cross a river,
from point A to point B, as shown in the
figure. The distance d1 (from
A to C) is 200 m, the distance d2
(from C to B) is 150 m, and the speed vr
of the current in the river is 5 km/hour. Suppose that the swimmer's velocity
relative to the water makes an angle of
θ = 45o with the line from A to C, as
indicated in the figure.
A swimmer wants to cross a river,
from point A to point B, as shown in the
figure. The distance d1 (from
A to C) is 200 m, the distance d2
(from C to B) is 150 m, and the speed vr
of the current in the river is 5 km/hour. Suppose that the swimmer's velocity
relative to the water makes an angle of
θ = 45o with the line from A to C, as
indicated in the figure.
To swim directly from A to B, what speed us, relative to the water,
should the swimmer have?
Solution:
- Concepts:
Kinematics
- Reasoning:
In the frame of the river bank, the time it takes the swimmer to move 200 m in the y direction (d1) has to be the same time taken to go 150m in the x direction (d2).
- Details of the calculation:
d2 = ∆x = vxt = (-us/√2 + vr)t,
d1 = ∆y = vyt = (us/√2 )t.
Here vx and vy are the swimmers velocity components
relative to the river bank.
d2/d1 = -1 + √2vr/us. us
= √2vr/(d2/d1 + 1)
d2/d1 = 3/4, us = 0.808*(5 km/hr) = 4.04 km/h =
1.12 m/s.
Problem:
Two ferries leave from opposite sides of a river. They
move with different speeds and meet 400 m from the left bank. Each continues to
its destination, take 5 minutes to unload and load, and then starts the return
trip. The ferries meet again 200 m from the right bank. How wide is the river?
Solution:
- Concepts:
Kinematics
- Reasoning:
Kinematics gives us two expression for the ratio vB/vA,
one for the initial and one for the return trip. Setting these equal
to each other allows us to solve for the width W of the river.
- Details of the calculation:
Let ferry B start from the left bank and ferry A start from the right
bank.
vBt1 = W - 400 m, vAt1 = 400 m
vB(t2 - 5 min) = 2W - 200 m, vB(t2
- 5 min) = W + 200 m
vB/vA = (2W - 200 m)/(W + 200 m) = (W - 400 m)/(400 m)
Solve for W: W2 - (1000 m)W = 0, W = 1000 m







 A swimmer wants to cross a river,
from point A to point B, as shown in the
figure. The distance d1 (from
A to C) is 200 m, the distance d2
(from C to B) is 150 m, and the speed vr
of the current in the river is 5 km/hour. Suppose that the swimmer's velocity
relative to the water makes an angle of
θ = 45o with the line from A to C, as
indicated in the figure.
A swimmer wants to cross a river,
from point A to point B, as shown in the
figure. The distance d1 (from
A to C) is 200 m, the distance d2
(from C to B) is 150 m, and the speed vr
of the current in the river is 5 km/hour. Suppose that the swimmer's velocity
relative to the water makes an angle of
θ = 45o with the line from A to C, as
indicated in the figure.