Interacting objects, Newton's 2nd and 3rd laws, conservation laws

Newton's second law

Problem:

Two masses (m₁ = 15 kg and m₂ = 20 kg) are connected by a massless cord and placed on a horizontal, frictionless surface.  The two-mass system is pulled to the right by a force F_A = 60 N using a cord that makes an angle of 40 degrees with the horizontal.  The masses remain on the horizontal surface.  There is no vertical motion.

(a)  Draw the free body diagrams for the two masses, properly labeling all forces.
(b)  What is the normal force between mass m₂ and the horizontal surface?
(c)  What is the acceleration of the system?
(d)  What is the tension F_T in the cord between the two masses?

Problem:

A 100 kg man climbs a vertical rope with an acceleration of 12 cm/sec².  Find the tension in the rope.

Solution:

• Concepts:
  Newton's 2^nd and 3^rd laws
• Reasoning:
  Man pulls on rope --> rope pulls on man.  F_net(upward) on man  = T - mg = ma.
• Details of the calculation:
  T = mg + ma = 100kg (9.8 + 0.12) m/s² = 992 N.

Problem:

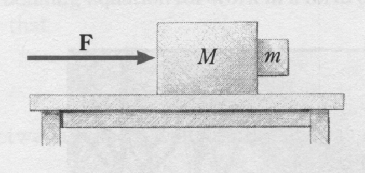
The force F in the figure below pushes a block of mass M = 5 kg, which in turn pushes a block of mass m = 1 kg.  There is no friction between M and the supporting surface.  If the friction coefficient between the two blocks is μ, how large must F be if the block of mass m is not to slip?

Solution:

• Concepts:
  Newton's laws, gravity, friction
• Reasoning:
  The gravitational force on m is F_g = mg in the negative y direction.
  The maximum force of static friction is f_s = μ_sN in the positive y direction.
  We want mg = μ_sN.
• Details of the calculation:
  The normal force accelerates m.  N = ma.
  The acceleration is given by a = F/(M + m).
  We therefore need mg = μ_s m F/(M + m).
  The minimum applied force F is given by  F = g(M + m)/μ_s. 

Problem:

Consider the system of 3 masses shown below.

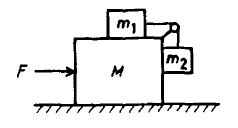
Assume all surfaces to be frictionless and the inertia of pulley and cord to be negligible.  Find the horizontal force necessary to prevent any relative motion of M, m₁, and m₂.

Solution:

• Concepts:
  Newton's laws, gravity
• Reasoning:
  If there is no relative motion of the masses, then all three masses have the same horizontal acceleration.
  The vertical component of the net force on m₂ must be zero.
• Details of the calculation:
  For the total mass:  F = (M + m₁ + m₂)a
  For the masses individually:  m₁a = T,    m₂g = T --> a = m₂g/m₁. 
  
  F = (M + m₁ + m₂)m₂g/m₁.

Problem:

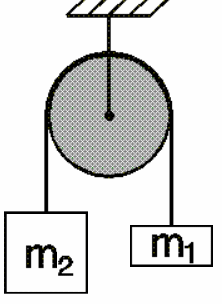
Near the surface of Earth, two masses, m₁ = 1 kg and m₂ = 3 kg, are connected by a string of negligible mass.  The masses hang on opposite sides of a pulley with radius R.  The pulley is fixed, and the string can slide over the pulley.
(a)  Find the acceleration of the masses if there is no friction between the string and the pulley.
(b)  Find the acceleration of the masses if the coefficient of kinetic friction between the string and the pulley is μ = 0.1.

Solution

• Concepts:
  Interacting objects,  Newton's laws
• Reasoning
  The frictional force in part (b) is proportional to the normal force.  We have to find the normal force a small section of rope exerts on the cylinder.
• Details of the calculation:
  (a)  The tension is the same everywhere in the string.  The mass m₂ will accelerate downward and the mass m₁ will accelerate upward with acceleration a.
  m₂g - T = m₂a.  T - m₁g = m₁a.  a = g(m₂ - m₁)/m₂ + m₁) = (9.8 m/s²)/2 = (4.9 m/s²).
  (b)
  
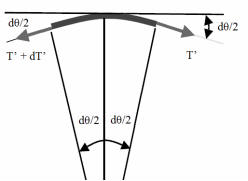
  Consider an infinitesimally small section of string of length Rdθ, acted on by the forces T'' = T' + dT' and T' as shown. 
  The magnitudes of the tangential and normal components of these forces are
  T'_t = T'cos(dθ/2), T'_n = T'sin(dθ/2), T''_t = T''cos(dθ/2), T''_n = T''sin(dθ/2).
  The magnitude of the net tangential force is T''_t - T'_t = dT'cos(dθ/2) = dT'.
  The magnitude of the net normal force is N = (2T' + dT')sin(dθ/2) = T'dθ since dθ is infinitesimal and we only keep first order terms in the small quantities.
  Since the string has negligible mass, dT' = μN = μT'dθ,  dT'/T' = μdθ, 
  Integrating from θ = 0 to θ = π we find ln (T₂/T₁) = μπ,  T₂/T₁ = exp(μπ).
  m₂g - T₂ = m₂a.  T₁ - m₁g = m₁a.  T₁ = T₂exp(-μπ).
  a = g(m₂exp(-μπ) - m₁)/m₂exp(-μπ) + m₁) = (9.8 m/s²)*0.37= (3.7 m/s²).

Problem:

Consider a glass that is resting on top of a tablecloth.  The glass has mass m₁ and the tablecloth has mass m₂.  Suppose the coefficient of static friction between the tablecloth and glass is given by μ_s, and the table is highly polished so it is nearly frictionless.
What is the maximum force that the tablecloth can be pulled horizontally so that the glass and table cloth move together without slipping?

Solution:

• Concepts:
  Newton's 2^nd and 3^rd laws
• Reasoning:
  Let us draw a free-body diagram.
  
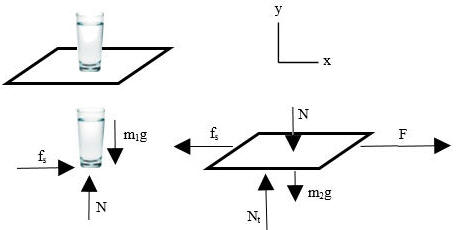
• Details of the calculation:
  (a)  x-direction: F - f_s = m₂a.
  f_s = m₁a.
  y-direction:  f_{s max} = μ_sN = μ_sm₁g.
  Combining:  (F - f_s)/m₂ = f_s/m₁,  F_max/m₂ = μ_sm₁g(1/m₁ + 1/m₂).
  F_max = μ_s(m₁ + m₂)g.

Problem:

A light flat ribbon is placed over the top of a triangular prism as shown in the diagram.   Two blocks are placed on the ribbon.   The coefficients of static and kinetic friction between the ribbon and the blocks are μ_s and μ_k, respectively.  There is no friction between the ribbon and the prism.  The angle θ and the masses of the blocks m and M are given.  Assuming that M > m, find the acceleration of the ribbon along the prism after the blocks are simultaneously released.  Consider all possible cases.

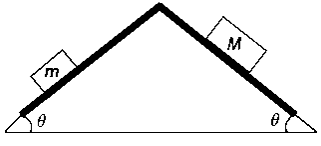
Solution:

• Concepts:
  Newton's second law, friction
• Reasoning:
  There are two scenarios.
  (i)  If θ < θ_c, where θ_c is some critical angle, then neither block will slide on the ribbon.  The ribbon will pull on the blocks (by means of static friction) with a tension force T.   The smaller block then accelerates uphill and the bigger one accelerates downhill with the same acceleration.
  (ii)  If θ < θ_c, then the smaller block will slide while the ribbon sticks to the larger block. (Since the ribbon is massless, the forces of friction exerted on it by each block must always have equal magnitudes.  Therefore, as a function on θ, the static friction limit is always be reached first by the smaller block, and the larger block never slides along the ribbon.)
• Details of the calculation:
  (i)  Assume neither block slides on the ribbon.
  a = (T - mg sinθ)/m = (Mg sinθ - T)/M.
  Solving for the unknown tension,
  T = 2g sinθ[Mm/(M + m)].  Therefore
  a = {[2g sinθ][Mm/(M + m)] - mg sinθ}/m = (g sinθ)[M - m)/(M + m)].
  The critical θ_c is reached when the ribbon tension becomes equal to the smaller block's static friction limit.  In that limiting case we have
  2g sin θ_c [Mm/(M + m)] = μ_smg cosθ_c,  tan θ_c = (μ_s/2)(1 + m/M).
  
  (ii)  When the smaller block is sliding, the ribbon tension is equal to the sliding friction between the smaller block and the ribbon, T = μ_kmg cosθ.
  The bigger block and ribbon then have downhill acceleration given by
  a = [Mg sinθ - μ_kmg cosθ]/M = g[sinθ - μ_k(m/M) cosθ].
  As the ribbon slides uphill under it, the smaller block has downhill acceleration given by:
  a = [mg sin θ - μ_kmg cos θ]/m = g (sinθ - μ_k cos θ).
  (If μ_k > tan θ, then the smaller block's acceleration will be negative, i.e. uphill.)

Newton's third law

Problem:

Sandra, who has a mass m = 40 kg stands on a M = 28 kg flatboat.  Her distance to the shore is 9.4 m.  She walks 2.6 m along the boat toward the shore and then stops.  How far is she away from the shore?  Assume there is no friction between the boat and the water.

Solution:

• Concepts:
  Newton's third law
• Reasoning:
  As she walks a distance d₁ towards the shore the boat moves a distance d₂ away from the shore.  The center of mass does not move.
• Details of the calculation:
  With respect to the shore:  md₁ = Md₂.  d₁ = (2.6 - d₂).
  40 kg(2.6 - d₂) = 28 kg d₂,
  68 kg d₂ = 40 kg 2.6 m,
  d₂ = 1.53 m.
  She has walked 1.07 m towards the shore.  Therefore she is now 8.33 m from the shore.

Problem:

A cat and a dog are sitting on the top of a small wagon which is a rest.  The mass of the dog is 20 kg and the mass of the cat is 5 kg.  There is no friction between the wagon and the ground.  The cat jumps from the wagon and then the dog jumps in the same direction from the already moving wagon.  When the dog jumps off, the wagon's velocity increases seven fold.  The horizontal components of the dog's and the cat's velocities before touching the ground are the same.  What is the wagon mass?

Solution:

• Concepts:
  Momentum conservation
• Reasoning:
  If no external forces act on a system along some axis, the component of the total momentum of the system along that axis is constant.
• Details of the calculation:
  Let the motion occur along the x-axis.  Let p and v refer to magnitude of the x-components of the momentum and the velocity, respectively, with respect to the ground.  p_total = 0.  Let M denote the mass of the wagon.
  cat jumps off:  -(5 kg)v_cat + (M + 20 kg)v₁ = 0.  v_cat = (M + 20 kg)v₁/(5 kg).
  dog jumps off:  -(20 kg)v_cat + 7Mv₁ = (M + 20 kg)v₁.
  (The dog and the cat have the same speed relative to the ground.)
  -4(M + 20 kg) + 7M = (M + 20 kg). 
  M = 50 kg.

Conservation laws

Problem

Two blocks of mass M and 3M are placed on a horizontal frictionless surface.  A light spring is attached to one of them, and the blocks are pushed together with the spring between them.  A cord holding them together is burned, after which the block of mass 3M moves to the right with a speed of 2 m/s.
(a) What is the speed of the block of mass M?
(b) Find the original elastic potential energy in the spring if M = 0.35 kg.

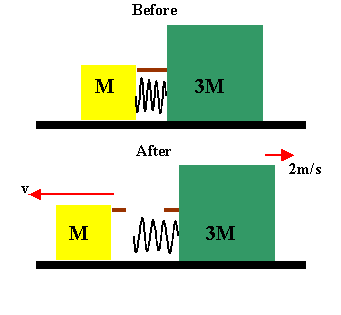
Solution:

• Concepts:
  Conservation of momentum, conservation of energy
• Reasoning:
  The total initial momentum of the system is zero.  No outside force act on the system in the horizontal direction, so the final horizontal momentum component of the system is also zero.
  The total energy E = T + U of the system is conserved.
• Details of the calculation:
  (a) conservation of momentum:
  p_3M + p_M = 0.
  p_3M = 3M (2 m/s), p_M = -3M ( 2m/)s = -6M m/s. v_M =  -6 m/s. 
  The block of mass M moves towards the left with a speed of 6 m/s.
  (b) conservation of energy:
  After the string has been cut and the spring has relaxed, E = T = ½3M(2 m/s)² + ½M(6 m/s)² = 8.4 J. 
  Initially E = U = 8.4 J, the total energy is the elastic energy stored in the spring.

Problem:

If two objects collide and one is initially at rest, is it possible for both to be at rest after the collision?  Is it possible for one to be at rest after the collision?  Explain!

Solution:

• Concepts:
  Conservation of momentum
• Reasoning:
  If a component of the total external force acting on a system is zero, then the corresponding component of the total momentum is conserved.
• Details of the calculation:
  In collisions between two objects momentum is conserved.  Since the initial momentum is not zero, the final momentum is not zero.  Both objects cannot be at rest.
  It is possible for one of the objects to be at rest after the collision.  For example, if the masses of the two objects are equal, then after a head-on elastic collision the object initially at rest is moving and the object initially moving is at rest.

Problem:

A sled on which you are riding is given an initial push and slides across frictionless ice.  Snow is falling vertically (in the frame of the ice) on the sled.  Assume that the sled travels in tracks which constrain it to move in a straight line.  Which of the following three strategies causes the sled to move the fastest?
(i)  You sweep the snow off the sled so that it leaves the sled in the direction perpendicular to the sled's tracks, as seen by you in the frame of the sled.
(ii)  You sweep the snow off the sled so that it leaves the sled in the direction perpendicular to the sled's tracks, as seen by someone in the frame of the ice.
(iii) You do nothing.
Order the strategies from best to worst and explain the ordering.

Solution:

• Concepts:
  Conservation of momentum:
• Reasoning:
  There are no external horizontal forces on the sled and the snow, so the total momentum of the sled plus the snow is constant in time.
• Details of the calculation:
  From best to worst, the ordering of the strategies is (ii), (iii), (i).
  Strategy (ii) beats strategy (iii).  The snow in (ii) ends up with no forward momentum, while the snow in (iii) continues to move forward with the sled.  The snow in (ii) therefore has less forward momentum than the snow in (iii), so the sled in (ii) must have more forward momentum than the sled in (iii).
  Strategy (iii) beats strategy (i).  When a snowflake is brushed off the sled in strategy (i), it initially has the same forward speed as the sled as they both sail across the frictionless ice.  But when the next snowflake hits, the brushed-off sled-snowflake system has less mass than the not brushed system, and therefore slows down more.