Conservation of angular momentum
Problem:
A child of mass 25 kg stands at the edge of a rotating platform of mass 150
kg and radius 4.0 m. The platform with the child on it rotates with an angular
speed of 6.2 rad/s. The child jumps off in a radial direction (i.e. has no
tangential velocity in the inertial frame of an outside observer). What happens
to the angular speed of the platform? Treat the platform as a uniform disk.
Give a quantitative explanation.
Solution:
- Concepts:
Conservation of angular momentum
- Reasoning:
The angular momentum of two interacting objects is constant.
- Details of the calculation:
(Iplatform + Ichild)ωi = Iplatformωf.
Iplatform = ½ 150kg (4m)2 = 1200 kgm2, Ichild
= 25kg (4m)2 = 400 kgm2.
ωf = 8.27 rad/s.
Problem:
A 60 kg woman stands at the rim of a horizontal turntable having a moment of
inertia of 500 kgm2, and a radius of 2 m. The turntable is
initially at rest and is free to rotate about a frictionless vertical axis
through its center. The woman then starts walking around the rim clockwise
(as viewed from above the system) at a constant speed of 1.5 m/s relative to the
Earth.
(a) In what direction and with what angular speed does the
turntable rotate?
(b) How much work does the woman do to set herself
and the turntable in motion?
Solution:
- Concepts:
Conservation of angular momentum
- Reasoning:
The system consists of the woman and the turntable. No
external torques act on the system, so the total angular momentum of the
system is conserved. It is zero before the woman starts to walk, and it is
zero afterwards.
- Details of the calculation:
(a) When the women walks with angular
velocity
ω = -(v/r)k = -((1.5 m/s)/(2 m))k =
-(0.75/s)k,
her angular momentum is
L = Iω = (-60
kg 4 m2 0.75/s)k = -(180 kgm2/s)k.
The angular momentum of the turntable will be
L = (180 kgm2/s)k,
its angular velocity
ω = (180 kgm2/s)k/(500 kgm2)
= (0.36/s)k. The turntable rotates counterclockwise.
(b) The
kinetic energy of the women is ½Iω2 = ½240 kgm2(0.75
s)2 = 67.5 J.
The kinetic energy of the turntable is ½Iω2
= ½500 kgm2(0.36 s)2 = 32.4 J.
The work
done by the women is W = (67.5 + 32.4) J = 99.9 J.
Problem:
A mass M is attached to the end of a string which passes through a hole in a
frictionless horizontal plane. Initially the mass moves on a circle of radius R
with kinetic energy T0. The string is then slowly pulled so that the
mass finally rotates on a circle of radius R/3. How much work was done?
Solution:
- Concepts:
Conservation of angular momentum
- Reasoning:
We have a force directed towards the center of the orbit. Therefore the torque
is zero.
- Details of the calculation:
Initial angular momentum: Li = mRv0 = mR(2T0/m)½.
Final angular momentum: Lf = mRvf /3 = m(R/3)(2Tf/m)½.
Conservation of angular momentum: Li = Lf,
mR(2T0/m)½ = m(R/3)(2Tf/m)½, T0
= Tf/9, Tf = 9 T0. Work done: Tf
- T0 = 8 T0.
Problem:
A small ball swings in a
horizontal circle at the end of a cord of length L1 which forms an
angle θ1 with the vertical.
Gravity is acting downward. The cord is slowly shortened by pulling it through
a hole in its support until the free length is L2 and the ball is
moving at an angle θ2 from
the vertical.
(a) Derive a relation between
L1, L2, θ1, and θ2.
(b) If L1 = 50 cm, θ1 = 5o, and L2
= 30 cm, find θ2.
Solution:
- Concepts:
Conservation of angular momentum
- Reasoning:
The applied force produces no torque.
- Details of the calculation:
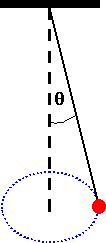
Initial
motion: T1cosθ1
= mg, T1sinθ1
= mv12/r = mv12/(L1sinθ1),
v12 = gL1sin2θ1/cosθ1.
Final motion : v22
= gL2sin2θ2/cosθ2.
Conservation of angular momentum: mL1sinθ1v1
= mL2sinθ2v2,
L12sin2θ1v12
= L22sin2θ2v22.
Therefore L13sin3θ1tanθ1
= L23sin4θ2tanθ2.
(b) Small angle approximation
L13θ14
= L23θ24, θ24 = 2.68*10-4,
θ2
= 0.128 rad = 7.33o.
Problem:
A point mass m attached to the end of a string revolves in a circle of radius
R on a frictionless table at constant speed with initial kinetic energy E0.
The string passes through a hole in the center of the table and the string is
pulled down until the radius of the circle is ½ of its initial value. Assuming
no external torque acts on the system, how much work is done?
Solution:
- Concepts:
Conservation of angular momentum
- Reasoning:
A radial force does not exert a torque about the origin.
- Details of the calculation:
E0 = ½mR2ω2,
L = mR2ω = (2mE0)½R.
After the radius
has been reduced to ½R, L = (2mEf)½R/2.
(2mE0)½R
= (2mEf)½R/2. 4E0 = Ef. The
work done on the system is 3E0.
(Or, E0 = ½mv2,
L = mvR = mvfR/2. So vf = 2v, Ef = ½mvf2
= 4E0. W = 4E0 - E0 = 3E0.)
Problem:
A solid sphere toy globe of mass M and radius R rotates freely without
friction with an initial angular velocity ω0. A bug of
mass m starts at one pole N and travels with constant speed v to the other pole
S along a meridian in time T. The axis of rotation of the globe is held
fixed. Show that during the time the bug is traveling the globe rotates
through an angle
Δθ = (πω0R/v) (2M/(2M + 5m))1/2.
Useful integral: ∫02πdx/(a + b cosx) = 2π/(a2
- b2)1/2, (a2 > b2).
Solution:
- Concepts:
Conservation of a component of the angular momentum
- Reasoning:
The axis of rotation is held fixed, so external forces
cannot be excluded. But holding an axis fixed cannot exert a torque about
this axis. So the component of angular momentum about the axis of rotation
is conserved.
- Details of the calculation:
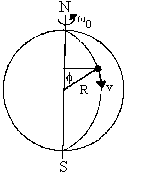
Lz
= Iω = I0ω0 = constant.
I0 = (2/5)MR2,
I = I0 + mR2sin2φ.
I(t)ω(t) = [(2/5)MR2
+ mR2sin2φ](dθ/dt) = (2/5)MR2ω0.
constant speed: φ = vt/R.
(dθ/dt) = (2/5)MR2ω0/[(2/5)MR2
+ mR2sin2(vt/R)].
Δθ = ∫0Tdt
(2/5)MR2ω0/[(2/5)MR2 + mR2sin2(vt/R)].
Change variables: x = 2vt/R, sin2(x/2) = ½(1 - cosx), since
∫dx/(a + b cosx) is an integral found in integral tables and is given
here..
Use vT/R = π.
Δθ = (Rω0/v)∫02πdx/[2
+ (5m/M) sin2(x/2)]
= (Rω0/v)∫02πdx/[2
+ (5m/(2M))(1 - cosx)]
= (πRω0/v)(2M/(2M + 5m))1/2.
As m --> 0, Δθ --> πω0R/v = ω0T, which corresponds to
the free rotation of the globe with angular speed ω0.
Problem:
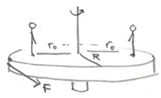 A playground merry-go-round has a radius of R = 4.0 m and has a moment of
inertia ICM = 7.0*103 kgm2 about a vertical
axis passing through the center of mass. There is negligible friction about
this vertical axis. Two children each of mass m = 25 kg are standing on
opposite sides a distance r0 = 3.0 m from the central axis. The
merry-go-round is initially at rest. A person on the ground applies a constant
tangential force of F = 2.5*102 N at the rim of the merry go-round
for a time ∆t = 10 s.
A playground merry-go-round has a radius of R = 4.0 m and has a moment of
inertia ICM = 7.0*103 kgm2 about a vertical
axis passing through the center of mass. There is negligible friction about
this vertical axis. Two children each of mass m = 25 kg are standing on
opposite sides a distance r0 = 3.0 m from the central axis. The
merry-go-round is initially at rest. A person on the ground applies a constant
tangential force of F = 2.5*102 N at the rim of the merry go-round
for a time ∆t = 10 s.
(a) What is the angular acceleration of the
merry-go-round?
(b) What is the angular velocity of the merry-go-round when the person stops
applying the force?
(c) What average power did the person put out while pushing the merry-go-round?
(d) What is the rotational kinetic energy of the merry-go-round when the person
stops applying the force?
The two children then walk inward and stop a distance of r1 = 1.0 m
from the central axis of the merry-go-round.
(e) What is the angular velocity of the merry-go-round when the children reach
their final position?
(f) What is the change in rotational kinetic energy of the merry-go-round when
the children reach their final position? Is this change positive or negative?
Solution:
- Concepts:
Rotational motion, conservation of angular momentum
- Reasoning:
The angular momentum of interacting objects is constant.
- Details of the calculation:
(a) τ = Itotα. Itot = ICM + 2*25*9 kgm2
= 7450 kgm2.
τ = RF = 1000 Nm, α = 0.134 rad/s2.
(b) ωf = α∆t = 1.34 rad/s.
(c) <P> = τωf/2 = 671 W.
(d) Trot = ½Itotωf2 = 6.71*103
J.
(e) L = Itotωf = Itot-newωf-new,
Itot-new = ICM + 2*25*1 kgm2 = 7050 kgm2,
ωf-new = 1.42 rad/s.
(f) Trot-new = ½Itot-newωf-new2 =
7.09*103 J. ∆Trot = 381 J. The rotational kinetic
energy has increased.
A uniform spherical planet of radius a revolves around the sun in
a circular orbit of radius r0 and angular velocity
ω0. It rotates about its axis with
angular velocity Ω0 (period T0)
normal to the plane of the orbit. Due to tides raised on the planet by the
sun, its angular velocity of rotation is decreasing. Find an expression
which gives the orbital radius r as a function of the angular
velocity Ω of rotation and the parameters r0 and T0 at any later or earlier time.


 A playground merry-go-round has a radius of R = 4.0 m and has a moment of
inertia ICM = 7.0*103 kgm2 about a vertical
axis passing through the center of mass. There is negligible friction about
this vertical axis. Two children each of mass m = 25 kg are standing on
opposite sides a distance r0 = 3.0 m from the central axis. The
merry-go-round is initially at rest. A person on the ground applies a constant
tangential force of F = 2.5*102 N at the rim of the merry go-round
for a time ∆t = 10 s.
A playground merry-go-round has a radius of R = 4.0 m and has a moment of
inertia ICM = 7.0*103 kgm2 about a vertical
axis passing through the center of mass. There is negligible friction about
this vertical axis. Two children each of mass m = 25 kg are standing on
opposite sides a distance r0 = 3.0 m from the central axis. The
merry-go-round is initially at rest. A person on the ground applies a constant
tangential force of F = 2.5*102 N at the rim of the merry go-round
for a time ∆t = 10 s.