Lagrangian problems, constrained point masses

Problem:

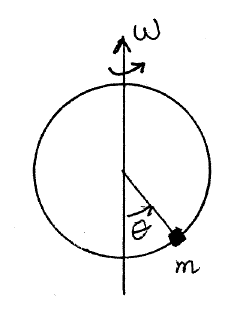
A circular hoop of radius r rotates with angular frequency ω about a vertical axis through the center of the hoop in the plane of the hoop.  A bead of mass m slides without friction around the hoop and is subject to gravity.
(a)  Give the Lagrangian in terms of the angle θ shown in the drawing.
(b)  Find the equation of motion in terms of this angle.
(c)  Find the values of θ for which the bead may be stationary with respect to the hoop and determine which of the stationary points are stable.

Solution:

• Concepts:
  Lagrange's equations
• Reasoning:
  Lagrange's equations are the equations of motion.
• Details of the calculation:
  (a)  L = T - U. 
  T = ½m(r²(dθ/dt)² + r²sin²θ ω²),  U = -mgr cosθ.
  L =  ½m(r²(dθ/dt)² + r²sin²θ ω²) + mgr cosθ.
  Here r and ω are constants.
  
  (b)  d/dt(∂L/∂(dq_i/dt)) -  ∂L/∂q_i = 0.
  ∂L/∂(dθ/dt) = mr²(dθ/dt),  ∂L/∂θ = mr²sinθ cosθ ω² - mgr sinθ.
  mr²d²θ/dt² - mr²sinθ cosθ ω² + mgr sinθ = 0.
  d²θ/dt² = sinθ cosθ ω² - (g/r) sinθ.
  
  (c)  d²θ/dt²|_θequ = 0 for a stationary point.
  The angles θ = 0, θ = π, or cosθ  = g/(rω²) define stationary points.
  We need g/(rω²) < 1 for the point θ = cos^-1(g/(rω²) to exist.
  
  For a stable point we need a restoring force.  Let θ = θ_equ + δ.
  We need d²δ/dt² = -cδ, with c a positive number.
  d²δ/dt²  = sin(θ_equ + δ)cos(θ_equ + δ) ω² - (g/r) sin(θ_equ + δ)
  = d(sinθ cosθ ω² - (g/r) sinθ)/dθ|_θequ*δ  (Taylor series expansion)
  = (cos²θ_qequ ω² - sin²θ_θequ ω² - (g/r) cosθ_θequ)δ.
  For a stable point we need cos²θ_θequ ω² - sin²θ_θequ ω² - (g/r) cosθ_θequ to be negative.
  Check:
  For the stationary point θ_θequ = 0:
  cos²θ_θequ ω² - sin²θ_θequ ω² - (g/r)cos θ_θequ = ω² - (g/r).
  If g/r > ω²  then this point is stable, otherwise it is unstable.
  For the stationary point θ_θequ = π:
  cos²θ_θequ ω² - sin²θ_θequ ω² - (g/r)cosθ_θequ = ω² + (g/r).
  This point is always unstable.
  For the stationary point θ_θequ = cos^-1(g/(rω²)):
  cos²θ_θequ ω² - sin²θ_θequ ω² - (g/r)cosθ_θequ = g²/(r²ω²) - ω² < 0 since g/(rω²) < 1 for the point to exist.
  This point is always stable if it exists.

Similar problems

Problem:

In the figure above the mass point m rotates about the point s.  At the same time the thread holding the mass point is shortened continuously.  Find the constants of motion.

Solution:

• Concepts:
  Lagrange's Equations
• Reasoning:
  All forces except the forces of constraint are derivable from a potential.  To find the constants of motion we find the Lagrangian and look for cyclic coordinates.
• Details of the calculation:
  Let x and y be the Cartesian coordinates in the plane of the circle and r and Ф be the polar coordinates. 
  r = R₀ - ct is equation of constraint.
  The constraint is holonomic and time dependent.
  x  = (R₀ - ct)cosФ, y = (R₀ - ct)sinФ. 
  T = ½m(v_x² + v_y²) = ½m((dФ/dt)²(R₀ - ct)² + c²).
  L = T,  we have only one generalized coordinate, Ф.
  ∂L/∂Ф = 0,  Ф is cyclic. 
  ∂L/∂(dФ/dt) = m(dФ/dt)(R₀ - ct)² = constant, since  (d/dt)(∂L/∂(dФ/dt)) = 0.
  The angular momentum about the vertical axis is conserved.

Problem:

An object of mass m slides on a horizontal, friction-free horizontal table.  A light, inextensible string, which passes through a small hole in the table, attaches the mass to a second body of mass M.  The second body hangs below the table where g = -9.8 m/s² (see the sketch).  At time t = 0, mass m is located at position (r, θ).

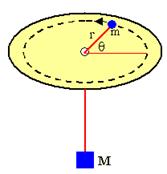
(a)  Determine the differential equations governing the motion of the system.
(b)  For the special case that r = constant, solve the resulting equations and interpret your results.
(c)  What are the constants of motion for this system?

Solution:

• Concepts:
  Lagrange's equations
• Reasoning:
  All forces except the forces of constraint are derivable from a potential.  To find the constants of motion we find the Lagrangian and look for cyclic coordinates.  If the generalized coordinates and momenta we choose do not depend on time and the Lagrangian does not depend explicitly on time, then the energy is a constant of motion.
• Details of the calculation:
  (a)  T = ½mr²(dθ/dt)² + ½(M + m)(dr/dt)²,   U = Mgr + U₀.  U₀ is an arbitrary constant.
  L = T - U,  ∂L/∂θ = 0, the coordinate θ cyclic, ∂L/∂(dθ/dt) = is a constant of motion.
  ∂L/∂(dθ/dt)  = mr²(dθ/dt) = C.
  Energy conservation leads to ½(M + m)(dr/dt)² + C²/(2mr²) + Mgr + U₀ = E.
  The first-order differential equations governing the motion of the system are
  ½(M + m)(dr/dt)² + C²/(2mr²) - Mg(L - r) = E,   mr²dθ/dt = C.
  The second-order differential equations governing the motion of the system are
  ∂(mr²(dθ/dt))/∂t = 0,   (M + m)d²r/dt² - C²/(mr³) + Mg = 0.
  (b)  r = constant = r₀,  dr/dt = 0.
  dθ/dt = ω = C/mr₀², the angular velocity is constant.
  E = ½m(r₀ω)² + Mgr₀ + U₀ = ½m(r₀ω)² = ½mv², if we choose U₀ = -Mgr₀.
  E is the kinetic energy for the circular motion.
  Mg = C²/(mr₀³) = mv²/r₀, Mg is the force responsible for the centripetal acceleration.
  (c)  The angular momentum about the vertical axis is a constant of motion.
  The energy E is a constant of motion.

Problem:

A rigid wire shaped like an upside-down L is spinning about its vertical segment as shown in the figure.

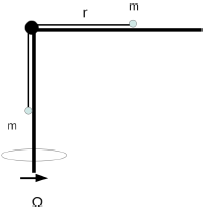
The angular velocity of the motion is Ω.  A bead of mass m is constrained to slide without friction on the horizontal segment of the wire and is connected by a massless string to an identical bead on the vertical segment.  The string has constant length l and follows the shape of the wire without friction.  The bead on the vertical segment is subjected to gravity (g is downward).
Consider only situations when this geometry is valid.
(a)  In terms of the distance r of the revolving bead from the center of rotation, write down the Lagrangian for this system.
(b)  Find the equation of motion for the bead.
(c)  Solve the equation of motion for the trajectory of the bead.

Solution:

• Concepts:
  Lagrangian Mechanics
• Reasoning:
  We are asked to obtain Lagrange's equation of motion and solve them..
• Details of the calculation:
  (a)  T = m(dr/dt)² + ½mr²Ω²,  U = -mg(l - r). 
  L = T - U = m(dr/dt)² + ½mr²Ω² + mg(l - r). 
  (b)   We have only one generalized coordinate, r.
  d/dt(∂L/∂(dr/dt)) - ∂L/∂r = 0.
  ∂L/∂(dr/dt) =  2m(dr/dt), d/dt(∂L/∂(dr/dt)) = 2m d²r/dt².
  ∂L/∂r = mrΩ² - mg.
  d²r/dt² = ½rΩ² - ½g  is the equation of motion.
  (c)  d²r/dt² = ar - b.
  Let r' = a(r - b/a), d²r'/dt² = ar'.
  r'(t) = C₁exp((√a)t) +  C₂exp(-(√a)t).
  r(t) = C₁exp((√a)t) +  C₂exp(-(√a)t) + b/a.
  The constants C₁ and C₂ are determined by the initial conditions. 

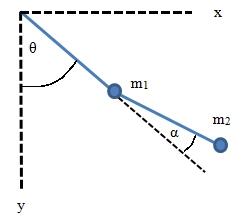
Problem:

Consider the double pendulum consisting of two massless rods of length L = 1 m and two point particles of mass m = 1 kg in free space, with a fixed pivot point.
(a)  Write down the Lagrangian of the system shown in terms of the coordinates θ and α shown and the corresponding velocities.
(b)  Find two conserved quantities.
(c)  Write down the second-order differential equations of motion.

Solution:

• Concepts:
  Lagrangian mechanics
• Reasoning:
  If one of the coordinates is cyclic, the conjugate momentum is conserved.
• Details of the calculation:
  (a)  L = T = ½ v₁² + ½ v₂²
  x₁ = sin(θ),   y₁ = cos(θ),   x₂ = sin(θ) + sin(θ + α),   y₂ = cos(θ) + cos(θ + α)
  v₁² = (dθ/dt)²_,
  v₂² = (dθ/dt)² + (dθ/dt + dα/dt)² + 2(dθ/dt)(dθ/dt + dα/dt)cos(α)
  L = (dθ/dt)² + ½(dθ/dt + dα/dt)² + (dθ/dt)(dθ/dt + dα/dt)cos(α)
  (b)  θ is cyclic, p_θ = constant.
  p_θ = ∂L/∂((dθ /dt)) = 2(dθ/dt) + (dθ/dt + dα/dt) + (dθ/dt + dα/dt)cos(α) + (dθ/dt)cos(α)
  = 3(dθ/dt) + (dα/dt) + 2(dθ/dt)cos(α) + (dα/dt)cos(α) = constant.
  L = T = E does not explicitly depend on time.
  E = (dθ/dt)² + ½(dθ/dt + dα/dt)² + (dθ/dt)(dθ/dt + dα/dt)cos(α) = constant.
  (c) dp_θ/dt = 0,  ∂L/∂((dα/dt)) -  ∂L/∂α = 0.
  This yield the two second order equations of motion below.
  (d²θ/dt²)(3 + 2 cos(α))  + (d²α/dt²)(1 + cos(α)) - 2(dθ/dt) (dα/dt)sin(α) - (dα/dt)²sin(α) = 0.
  (d²θ/dt²) + (d²α/dt²)cos(α) + (dθ/dt)² sin(α) = 0.

Problem:

A particle of mass equal to 3 kg moves in the xy plane.  The potential energy of the particle as a function of position is given by  U = (36 J/m²)xy - (48 J/m²)x².  The particle starts at time t = 0 from rest at the point with position vector (x, y) = (10 m, 10 m).
(a)  Set up the differential equations describing the motion and solve them to determine the position of the particle as a function of time.
(b)  Find the velocity as a function of time.

Solution:

• Concepts:
  Lagrange's Equations:  d/dt(∂L/∂(dq/dt)) -  ∂L/∂q = 0.
• Reasoning:
  The potential energy is given.  All forces except the forces of constraint are derivable from a potential.  The Lagrangian formalism is well suited for such a system.
• Details of the calculation:
  L = T - U = ½m((dx/dt)² + (dy/dt)²) - 36xy + 48x²  (SI units).
  ∂L/∂(dx/dt) = m(dx/dt),  ∂L/∂(dy/dt) = m(dy/dt),  ∂L/∂x = -36y + 96x,  ∂L/∂y = -36x.
  md²x/dt² + 36y - 96x = 0,  md²y/dt² + 36x = 0,  m = 3.
  d²x/dt² + 12y - 32x = 0,  d²y/dt² + 12x = 0.
  (a)  Let x = Aexp(at),  y = A'exp(at).
  Then a²A +12A' - 32A = 0,  a²A' + 12A = 0, a²A - 144A/a² -32A = 0.
  a⁴ - 32a² - 144 = 0,  a² = 16 ± 20.
  a² = 36, a = ±6 yields exponential solutions.
  a² = -4, a = ±2i yields sinusoidal solutions.
  If a² = 36, then A' = -(1/3)A.
  If a² = -4, then A' = 3A.
  The most general solution is a linear superposition of all possible solutions.
  x = a₁exp(6t) + a₂exp(-6t) + a₃cos(2t) + a₄sin(2t),
  y = -(a₁/3)exp(6t) - (a₂/3)exp(-6t) + 3a₃cos(2t) + 3a₄sin(2t).
  dx/dt = 6a₁exp(6t) - 6a₂exp(-6t) - 2a₃sin(2t) + 2a₄cos(2t),
  dy/dt = -2a₁exp(6t) + 2a₂exp(-6t) - 6a₃sin(2t) + 6a₄cos(2t).
  
  At t = 0 we have (dx/dt) = 0, (dy/dt) = 0, 3a₁ - 3a₂ + a₄ = 0, -a₁ + a₂ + 3a₄ = 0.
  At t = 0 we have x = 10, y = 10, a₁ + a₂ + a₃ = 10, -a₁ - a₂ + 9a₃ = 30.
  Four equations for four unknowns yield a₁ = 3, a₂ = 3, a₃ = 4, a₄ = 0.
  x(t) = 3exp(6t) + 3exp(-6t) + 4cos(2t) = 6cosh(6t) + 4cos(2t),
  y(t) = -exp(6t) - exp(-6t) + 12cos(2t) = -2cosh(6t) + 12 cos(2t).
  Below are contour and a surface plots of the potential for
  -12.5 < x < 12.5,
  -12.5 < y < 12.5.
  
  
  

  (b)  dx/dt = 18exp(6t) - 18exp(-6t) - 8sin(2t) = 36 sinh(6t) - 8sin(2t).
  dy/dt = -6exp(6t) + 6exp(-6t) - 24sin(2t) = -12sin

Problem:

Obtain Lagrange's equations of motion for a spherical pendulum (a mass point suspended by a rigid, weightless rod).

Solution:

• Concepts:
  Lagrange's Equations: d/dt(∂L/∂(dq_j/dt)) -  ∂L/∂q_j = 0; generalized coordinates
• Reasoning:
  We are asked to obtain Lagrange's equation of motion.  Let g point into the -z direction.
  
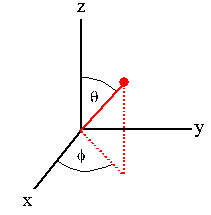
  The system has only two degrees of freedom.  Choose the generalized coordinates to be θ and Φ.  The constraints are holonomic, the applied forces are conservative.
• Details of the calculation:
  d/dt(∂L/∂(dq_j/dt)) -  ∂L/∂q_j = 0,  and  q₁ = θ,  q₂  = Φ.
  L = T - U
  T = ½m(r²(dθ/dt)² + r²sin²θ(dΦ/dt)²),  U = mg r cosθ.
  ∂L/∂(dθ/dt) = mr² dθ/dt,  d/dt(∂L/∂(dθ/dt)) = mr² d²θ/dt²,
  ∂L/∂θ = mr² sinθ cosθ(dΦ/dt)² +  mg r sinθ.
  ∂L/∂(dΦ/dt) = mr² sin²θ dΦ/dt,  
  d/dt(∂L/∂(dΦ/dt)) = mr² sin²θ d²Φ/dt² + 2mr² sinθ cosθ dθ/dt dΦ/dt,
  ∂L/∂Φ = 0.
  In this problem Φ is cyclic, ∂L/∂(dΦ/dt) is a constant of motion.
  sin²θ(dΦ/dt) = constant = C.  dΦ/dt = C/sin²θ.

  Equations of motion (second order differential equations):
  d²θ/dt² = sinθ cosθ(dΦ/dt)² + (g/r)sinθ = (cosθ/sin³θ)C² + (g/r)sinθ.
  d²Φ/dt² = -2 dΦ/dt dθ/dt cotθ = 2 C dθ/dt (cosθ/sin³θ) = 0.

  Note:
  Because Φ is cyclic, we already have a first integral. 
  We can insert dΦ/dt = C/sin²θ into the expressions for d²θ/dt² and d²Φ/dt².

Problem:

Consider a bead of mass m sliding freely on a smooth circular wire of radius b which rotates in a horizontal plane about one of its points O, with constant angular velocity Ω.  Let θ be the counterclockwise angle between the diameter that passes through the mass and the diameter that passes through the point O, with θ = 0 the case where the mass is farthest from O.

(a)  Find the equation of motion for θ.  Compare this equation with the equation of motion for a simple pendulum (point mass and massless rod).
(b)  For the initial conditions θ = 0, dθ/dt = ω₀ at t = 0, describe the θ motion that occurs for |ω₀| < 2Ω and for |ω₀| > 2Ω.  (Note:  The same equations have the same solutions.)
(c)  Describe the θ motion that occurs for |ω₀| << 2Ω.
(d)  Find the force that the wire exerts on the bead as a function of θ and dθ/dt.

Solution:

• Concepts:
  Lagrangian Mechanics
• Reasoning:
  All forces except the forces of constraint are derivable from a potential.  The Lagrangian formalism is well suited for such a problem.
• Details of the calculation:
  (a)  Let Ωt be the angle between the diameter going through the rotation point O and the x-axis.  Then we may write the Cartesian coordinates of the mass as
  x = bcos(Ωt) + bcos(θ + Ωt),  y = bsin(Ωt) + bsin(θ + Ωt).
  T = ½m((dx/dt)² + dy/dt)²) = ½mb²(Ω² + (Ω + ω)² + 2Ω(Ω + ω) cosθ),  where ω = dθ/dt.
  L = T.
  Lagrange's equation  d/dt(∂L/∂ω) - ∂L/∂θ = 0 yields
  d²θ/dt² + Ω²sinθ = 0.  A simple pendulum has the same equation of motion if we let Ω² = g/ℓ.
  
  (b)  Using the simple pendulum (point mass on a massless rod) as a guide we know that the θ motion is oscillatory if ½mℓ²ω₀² < 2mgℓ, or ω₀² < 4g/ℓ and the θ motion is circular if ω₀² < 4g/ℓ.  So for our problem the θ motion is oscillatory if ω₀² < 4Ω² and the θ motion is circular if ω₀² < 4Ω².
  
  (c)  If |ω₀| << 2Ω then sin(θ) ≈ θ and we have simple harmonic motion with a period T = 2π/Ω that does not depend on the amplitude.
  As |ω₀| increases, and approaches 2Ω the period increases and becomes very long near |ω₀| ≈ 2Ω.
  For |ω₀| > 2Ω the period (of the now circular motion) increases again and approaches T = 2π/|ω₀| for |ω₀| >> 2Ω.
  
  (d)  Use Lagrange multipliers.  Let r become a generalized coordinate.
  x = bcos(Ωt) + rcos(θ + Ωt),  y = bsin(Ωt) + rsin(θ + Ωt).
  T = ½m(b²Ω² + (dr/dt)² + r²(Ω + ω)² + 2bΩ(dr/dt)sinθ + 2brΩ(Ω + ω) cosθ) = L.
  The equation of constraint is r = b, dr = 0, 
  λ₁(a_1r dr + a_1θ dθ) = 0, a_1r  = 1, a_1θ = 0.
  Lagrange's equation for the r degree of freedom is d/dt(∂L/∂v_r) -  ∂L/∂r = λ₁a_1r = λ₁.
  λ₁ = F_r, the force that the wire exerts on the bead.
  F_r = -mb[Ω²cosθ + (Ω + ω)²].

Problem:

A bead, of mass m, slides without friction on a wire that is in the shape of a cycloid with equations
x = a(2θ + sin2θ),
y = a(1 - cos2θ),
- π/2 ≤ θ ≤ π/2.

A uniform gravitational field g points in the negative y-direction.
(a)  Find the Lagrangian and the second order differential equation of motion for the coordinate θ.
(b)  The bead moves on a trajectory s with elements of arc length ds.
Integrate ds = (dx² + dy²)^½ = ((dx/dθ)² + (dy/dθ)²)^½dθ with the condition s = 0 at θ = 0 to find s as a function of θ.
(c)  Rewrite the equation of motion, switching from the coordinate θ to the coordinate s and solve it.  Describe the motion.

Solution:

• Concepts:
  Lagrangian Mechanics
• Reasoning:
  We are asked to obtain Lagrange's equation of motion, using two different generalized coordinates.
• Details of the calculation:
  (a)  L = T - U.   T = ½m(v_x² + v_y²),  v_x = dx/dt = 2a(dθ/dt)(1 + cos2θ), 
  v_y = dy/dt = 2a(dθ/dt)sin2θ.
  T = 2ma²(dθ/dt)²[(1 + cos2θ)² + sin²2θ] = 4ma²(dθ/dt)²(1 + cos2θ)
  = 8ma²(dθ/dt)²cos²θ.
  U = mgy = mga(1 - cos2θ) = 2mga sin²θ.
  L = 8ma²(dθ/dt)²cos²θ - 2mga sin²θ.
  
  Lagrange's equations:  d/dt(∂L/∂(dq_i/dt)) -  ∂L/∂q_i = 0.
  We have only one generalized coordinate.
  ∂L/∂(dθ/dt)) = 16ma²(dθ/dt)cos²θ.
  d/dt(∂L/∂(dθ/dt)) = 16ma²d²θ/dt²cos²θ - 32ma²(dθ/dt)²cosθ sinθ.
  ∂L/∂θ = -16ma²(dθ/dt)²cosθ sinθ - 4mga cosθ sinθ.
  Equation of motion: 
  16ma²d²θ/dt²cos²θ - 16ma²(dθ/dt)²cosθ sinθ + 4mga cosθ sinθ = 0.
  d²θ/dt²cosθ - (dθ/dt)²sinθ + (g/(4a)) sinθ = 0.

  (b)  ds = 4a cosθ dθ.  s(θ) = ∫₀^θds = ∫₀^θ4a cosθ'dθ' = 4a sinθ.

  (c)  ds/dt = 4a cosθ (dθ/dt).  d²s/dt² = 4a cosθ d²θ/dt² - 4a sinθ (dθ/dt)².
  Therefore d²θ/dt² cosθ - (dθ/dt)² sinθ = (4a)^-1d²s/dt²,
  and  (g/(4a))sinθ = (g/(4a)²)s.

  The equation of motion in terms of the coordinate s is d²s/dt² = -(g/(4a))s. 
  This is Hooke's law with the solution s(t) = s₀ cos(ωt + φ).

  ω = (g/(4a))^½, s₀ and φ depend on the initial conditions.
  The bead executes simple harmonic motion in s.