Driven and damped oscillations
Damped oscillations
Problem:
The differential equation describing the displacement from equilibrium for
damped harmonic motion is
md2x/dt2 + kx + cdx/dt = 0.
(a) State the conditions and find an expression for x(t) for underdamped,
critically damped, and overdamped motion.
(b) Show that for underdamped motion, the ration of two successive maxima in
the displacement x is constant.
Solution:
- Concepts:
The damped harmonic oscillator
- Reasoning:
For underdamped motion we have oscillations with and exponentially decreasing
amplitude. For critically and overdamped motion we have no oscillations and at
most one zero crossing as the system returns to equilibrium.
- Details of the calculation:
(a) Let x = Aexp(iΩt). (The real part is implied.) Then
-Ω2 + k/m + iΩc/m = 0, Ω = ic/(2m)
± (ω02 - c2/(2m)2)½,
with ω02 = k/m.
Let γ = c/(2m). Ω = iγ ± (ω02 - γ2)½. Let ω2
= (ω02 - γ2).
If ω02 > γ2, or k/m > c2/(2m)2,
then ω is real.
x = |A|exp(-γt)cos(ωt + δ), |A| and δ depend on the initial conditions.
We have underdamped motion.
If ω02 = γ2, then ω is zero, we have critically
damped motion
x = Aexp(-γt) is one solution to the differential equation d2x/dt2
+ γ2x + 2γdx/dt = 0,
x = Bt exp(-γt) is another solution.
[Assume the most general solution is x(t) = u(t)exp(-γt).
Inserting this into the differential equation yields d2u/dt2
= 0,
u(t) = constant or u(t) = constant*t.]
The most general solution is x = Aexp(-γt) + Bt exp(-γt).
A and B depend on the initial conditions.
If ω02 < γ2, then ω is imaginary, ω
= ±i(γ2 - ω02)½ = ±iβ.
We have overdamped motion.
x = Aexp(-(γ + β)t) + Bexp(-(γ - β)t). A and B depend on the initial
conditions.
(b) Maxima in the displacement (either in the positive or negative
x-direction) occur when
dx/dt = 0, -γcos(ωt + δ) - ωsin(ωt + δ) = 0,
tan(ωt + δ - nπ) = -γ/ω,
ωt = nπ - δ - tan-1(γ/ω) ∆t = (π/ω)
= time between two successive maxima.
The ratio of successive maximum values of x(t) is R = exp(-γπ/ω).
Problem:
A damped oscillator satisfies the equation d2x/dt2 +
2γdx/dt + ω02x = 0, where γ and ω0 are
positive constants with γ < ω0 (under-damping). Assume that the
equation of motion of a particle of mass m is given by this equation. At time t
= 0, the particle is released from rest at the point x = a.
(a) Find x as a function of time t and sketch of x as a function of t.
(b) Find all the turning points of the motion and determine the ratio of
successive maximum values of x(t).
(c) Re-do part( a) for the case of critical damping, i.e. when γ = ω0.
Solution:
- Concepts:
The
underdamped harmonic oscillator
- Reasoning:
For underdamped motion we have oscillations with and exponentially decreasing
amplitude. For critically and overdamped motion we have no oscillations and at
most one zero crossing as the system returns to equilibrium.
- Details of the calculation:
(a) d2x/dt2 = -ω02x
- 2γdx/dt.
Then the solution for underdamped motion is
x(t) = a exp(-γt) cos(ω1t + δ), with ω12
= ω02 - γ2.
Here ω0 is the angular frequency of an undamped
oscillator with the same spring constant and δ ~ 0 if γ << ω0,
(tanδ = - γ/ω1).
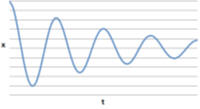
(b) Zeroth order
approximations: γ << ω0. The turning
points of the motion occur when
ω1t = (ω02 - γ2)½t
= nπ, cos(ω1t) = ±1. Then t = (nπ/ω1).
The ratio of successive maximum values of |x(t)| is R = exp(-γ(t + ∆t)/exp(-γt)
= exp(-γ∆t),
where ∆t = (π/ω1). R = exp(-γπ/ω1). ω1 ≈
ω0(1 - ½γ2/ω02).
Higher order: dx/dt = 0. -γcos(ω1t) - ω1sin(ω1t)
= 0, tan(ω1t - nπ) = -γ/ω1,
ω1t = nπ - tan-1(γ/ω1) ∆t = (π/ω1).
The turning points of the motion occur when t = nπ/ω1 - tan-1(γ/ω1)/ω1,
earlier than t = nπ/ω1.
The ratio of successive maximum values of |x(t)| stays R = exp(-γπ/ω1).
(c) When γ = ω0 then ω1 = 0 and x(t) = (a + bω0t)
exp(-ω0t).
Problem:
Consider a damped harmonic oscillator. Let us define T1 as
the time between adjacent zero crossings, 2T1 as its "period", and ω1
= 2π/(2T1) as its "angular frequency". If the amplitude of the
damped oscillator decreases to 1/e of its initial value after n periods, show
that the frequency of the oscillator must be approximately [1 - (8π2n2)-1]
times the frequency of the corresponding undamped oscillator.
Solution:
- Concepts:
The underdamped harmonic oscillator
- Reasoning:
The oscillator is underdamped, since it crosses the
equilibrium position many times.
- Details of the calculation:
The equation of motion for the damped
harmonic oscillator is d2x/dt2 + 2βdx/dt + ω02x
= 0.
The solution for underdamped motion is x(t) = A exp(-βt) cos(ω1t
- δ), with ω12 = ω02 - β2.
Here ω0 is the angular frequency of an undamped oscillator with
the same spring constant.
After n periods, nT = 2nT1, the
amplitude of the oscillator decreases to A/e.
So exp(-1) = exp(-βnT),
βnT = 1, β = 1/nT.
With T = 2π/ω1 we have β = ω1/(n2π).
ω12 = ω02 - (ω1/n2π.)2,
ω12 + ω12/(4n2π2)
= ω02.
ω1 = ω0 [1 + 1/(4n2π2)]-½.
(1 + x)-½ = 1 - ½ x + ... .
ω1 ≈ ω0 [1 -
1/(8n2π2)].
Problem:
A mass on a spring moves in one dimension and is subject to a
velocity-dependent force. The net force is F = -kx - bv. Assuming
is small, what fraction of energy is dissipated in each cycle?
Solution:
- Concepts:
The underdamped harmonic oscillator
- Reasoning:
The oscillator is underdamped, since it goes through many
cycles.
- Details of the calculations:
md2x/dt2 = -kx -
bdx/dt, d2x/dt2 = -(k/m)x - (b/m)dx/dt.
Let ω02
= k/m, β = b/2m.
Then the solution for underdamped motion is x(t) = A
exp(-βt) cos(ω1t - δ),
with ω12 = ω02
- β2.
Here ω0 is the angular frequency of an
undamped oscillator with the same spring constant.
The energy is
proportional to the square of the effective amplitude, (A exp(-βt))2.
After one cycle the amplitude decreases by a factor of exp(-βτ), where τ =
2π/ω1. The energy decreases by a factor of exp(-2βτ).
If β
is small, then exp(-2βτ) = 1 - 2βτ.
The fraction of the energy
dissipated in each cycle is
2βτ = (b/m)(4πm)/(4k - b2)½
= (4πb)/(4k - b2)½.
Problem:
The terminal speed of a freely falling object is
vt (assume the drag force is proportional to the speed of the
object). When the object is suspended by a spring, while still influenced by
the same drag force, the spring stretches by an amount x0. Show that
the frequency of oscillation of the object (when it is suspended by the spring)
is ω, where ω2 = g/x0 - g2/(4vt2).
Solution:
- Concepts:
The damped harmonic oscillator..
- Reasoning:
The equation of motion for the damped harmonic oscillator with the x-axis
pointing up is md2x/dt2 = -γdx/dt - kx - mg. Here x is
the displacement of the free end of the spring from its equilibrium position.
The terminal velocity vt lets us calculate γ, and x0 lets
us calculate the spring constant k.
- Details of the calculation:
When the system is not accelerating: mg = γvt, γ = mg/vt.
mg = kx0, k = mg/x0.
d2x/dt2 = -(g/vt)dx/dt - (g/x0)x -
mg.
Try a solution x = -x0 + A(exp(ict) for the equation of motion. Here
c = -iβ + ω
-mc2A(exp(ict) = -iγc A(exp(ict) + kx0 - kA(exp(ict) - mg.
c2 - i(γ/m)c - k/m = 0 .
c = -iγ/(2m) + (k/m - γ2/(4m2))½. ω2
= k/m - γ2/(4m2) = g/x0 - g2/(4vt2).
Problem:
Consider a pendulum consisting of a rigid thin rod with length L and
negligible mass supporting a ball of mass M. The pendulum is immersed in a
viscous medium which causes a frictional force F whose magnitude is proportional
to the speed v of the ball, F = -μv. It swings in a vertical plane under
the influence of gravity.
(a) Derive the equation of motion of the pendulum,
allowing for arbitrary angles θ of deflection from the vertical axis.
(b)
Determine the fixed points for which d2θ/dt2 = 0 when dθ/dt
= 0. Determine for each fixed point the critical value of the drag
coefficient μ above which there is no oscillation about the point for small
displacements.
Solution:
- Concepts:
Newton's
2nd law
- Reasoning:
Newton's second law gives the
equation of motion. We are asked to find the equilibrium points, where
the acceleration is zero. The equation of motion will tell us if small
displacements away from an equilibrium point will lead to oscillations.
- Details of the calculation:
F = Ma
(a) Equation of motion: MLd2θ/dt2 = -Mgsinθ -
μLdθ/dt
d2θ/dt2
+ (μ/M)dθ/dt + (g/L)sinθ = 0
(b) Fixed points: θ = 0 and θ =
π.
For small deviations from θ = 0 we have d2θ/dt2
+ (μ/M)dθ/dt + (g/L)θ = 0.
θ = θ0exp(iωt), ω2
- iωm/M - g/L = 0, ω = iμ/(2M) ± (-μ2/(4M2) +
g/L)½
= iα ± β.
(The displacement as a function of time is given by the real
part of this solution.)
If μ < 2M(g/L)½, then β is real and
θ = θ0exp(-αt) exp(±iβt), we have oscillations.
If μ > 2M(g/L)½,
then β is imaginary and we have no oscillations.
For small deviations
from θ = π we have d2φ/dt2 + (μ/M)dφ/dt - (g/L)φ = 0,
where φ = π + θ.
φ = φ0exp(λt), λ2 + λm/M -
g/L = 0, λ = -μ/(2M) ± (μ2/(4M2) + g/L)½.
λ is always real, we have no oscillations for any value of μ.
Problem:
A grandfather clock has a pendulum of length L = 1 m and a bob of mass m = 0.5
kg. A mass of 2 kg falls 0.7 m in seven days to keep the amplitude if the
pendulum oscillations steady at 0.03 rad.
(a) The quality factor Q of a damped oscillator is defined as
Q = 2π*(average energy)/(energy lost per cycle).
What is the Q of this system?
(b) With no energy input from the falling mass, the pendulum obeys the small
angle equation of motion
d2θ/dt2 + 2bdθ/dt + ω02θ = 0.
Find b and ω0.
Solution:
- Concepts:
The driven, damped oscillator
- Reasoning:
With no energy input, the oscillator is underdamped. The damping is weak.
- Details of the calculation:
(a) The rate at which energy is dissipated is
dE/dt = -(2 kg*9.8 m/s2*0.7 m)/(7*24*3600 s) = -2.3*10-5
J/s.
The average energy of an oscillator is E = ½kA2. Here k = mg/L and A
= Lθ.
E = ½*0.5 kg*9.8 m/s2*1 m*(0.03)2 = 2.2*10-3 J.
Since the rate of energy dissipation is small, the period of the pendulum is
nearly equal to its natural period T = 2π(L/g)½ = 2s.
Therefore Q = 2π*(2.2*10-3 J)/( 2.3*10-5 J/s*2s) = 300.
(b) ω0 = (g/L)½ = 3.13/s
Then the solution for underdamped motion is x(t) = A
exp(-βt) cos(ω1t + δ),
with ω12 = ω02 - β2.
The energy is proportional to the square of the effective amplitude, (A exp(-βt))2.
After one cycle the ration of the amplitudes is A(t + T)/A(t) = exp(-βT).
The ration of the energies is E(t + T)/E(t) = exp(-2βT).
If β is small, then exp(-2βT) = 1 - 2βT.
The fraction of the energy dissipated in each cycle is |(E(t + T) - E(t))/E(t) |
= 2βT.
2βT = 2π/Q. β = π/(2s*300) = 5.2*10-3
/s.
A mass m fixed to a spring of spring constant k and
immersed in a fluid provides a model for a damped harmonic oscillator. A
circuit with inductance L, capacitance C and resistance R provides an electric
analog to such an oscillator.
(a) Write out the circuit equation for the LCR circuit and Newton's second law
of motion for the damped oscillator. What assumption must be made about the
dependence of the damping of the mass on velocity for the two equations to have
the same mathematical form?
(b) How are the constants m, k, and b (damping constant) related to the circuit
constants L, C and R? To what parameters of the electric circuit are the
mechanical quantities x (displacement) and v (velocity) related?
(c) Derive and expression for the displacement and velocity in the limit of
weak damping.
(d) What voltages measured in the circuit would give values proportional to the
displacement and velocity of the mechanical oscillator?
Driven and damped oscillations
Problem:
Consider a damped harmonic oscillator. Let us define T1 as the
time between adjacent zero crossings, 2T1 as its "period", and ω1
= 2π/(2T1) as its "angular frequency". The damped harmonic
oscillator is characterized by the quality factor Q = ω1/(2β), where
1/β is the relaxation time, i.e. the time in which the amplitude of the
oscillation is reduced by a factor of 1/e.
(a) After 8.6 seconds and 5 periods of oscillations, the amplitude of a
damped oscillator decreased to 17% of its originally set value. Determine
the quality factor Q of the system.
(b) A motor now supplies an external driving term M cosωt. Determine
the stationary solution for the now driven and damped oscillator.
(c) For a system with an equation of motion
d2x/dt2 + 2β dx/dt + ω02x = A cos(ωt)
the quality factor Q is defined as Q = ωR/(2β), where ωR
is the angular frequency for amplitude resonance. Compare the shape of a
plot of the amplitude of the oscillations versus the driving frequency Ω for
the above driven and damped oscillator with a Lorentzian atomic line shape
for Q = 4 and Q = 107.
Solution:
- Concepts
The underdamped harmonic oscillator, the driven oscillator
- Reasoning:
The oscillator in part (a) is underdamped, since it crosses the equilibrium
position many times. For part (b) a harmonic driving force is given.
- Details of the calculations:
(a) The equation of motion for the damped harmonic oscillator is d2x/dt2
+ 2βdx/dt + ω02x = 0.
The solution for underdamped
motion is x(t) = A exp(-βt) cos(ω1t - δ), with ω12
= ω02 - β2.
Here ω0 is the
angular frequency of an undamped oscillator with the same spring constant.
Aexp(-β*8.6 s) = 0.17 A, -β*8.6 s = ln(0.17) , β = 0.206/s.
5(2T1) = 8.6 s, ω1 = 2π/(2T1) = 3.651, Q =
ω1/(2β) = 8.87.
(b) The equation of motion for the harmonically driven harmonic oscillator
(with damping) is d2x/dt2 + 2βdx/dt + ω02x
= Acosωt, with A = M/m.
The stationary solution x(t) = Dcos(ωt - δ) with
tanδ = 2ωβ/(ω02 - ω2) and D = A/[(ω02
- ω2)2 + 4ω2β2]½.
[The expressions for tanδ and D are found by substituting x(t) = Dcos(ωt -
δ) into the differential equation d2x/dt2 + 2βdx/dt +
ω02x = Acosωt.]
When ω = ωR
= [ω02 - 2β2]½ we have
amplitude resonance. [dD/dω = 0 when evaluated at ωR.]
For an undamped oscillator ωR = ω0 and Q = infinity.
The amplitude increases without limit when the driving frequency ω
approaches ω0.
(c) When Q = 4, we have ωR = 8β, so at amplitude resonance is D
≈ A/(2ωRβ) = 4A/ωR2.
When Q = 107, we have ωR = 2 107 β, so at
amplitude resonance D ≈ A/(2ωRβ) = 107A/ωR2.
The shape of the resonance curve approaches that of an undamped oscillator.
The figure below shows plots of amplitude versus driving frequency for
different values of β. (A = 1, ω0 = 10, β = 0.01 (blue), 0.1
(pink), 0.5 (orange).)

- Additional information:
For a lightly damped oscillator we have Q ≈ ω0/Δω, where Δω
represents points on the amplitude resonance curve that are 2-½
= 0.707 of the maximum amplitude.
Proof:
For a lightly damped oscillator ωR ≈ ω0 and Q ≈ ω0/(2β).
The amplitude at resonance is D ≈ A/(2ω0β). The driving
frequency for which the amplitude is 2-½ of the maximum
amplitude is found from A/(2-½2ωβ) = A/[8ω2β2]½
= A/[(ω02-ω2)2 + 4ω2β2]½.
8ω2β2 ≈ (ω02-ω2)2
+ 4ω2β2, 4ω2β2 = (ω02-ω2)2,
2ωβ = (ω02-ω2) = (ω0+ω)(ω0-ω).
2ωβ ≈ 2ωΔω/2, since (ω0+ω) ≈ 2ω0 near resonance.
This yields 2β ≈ Δω and Q ≈ ω0/Δω.
Q becomes large when Δω becomes small compared to ω0.
Problem:
A 0.500 kg mass is attached to a spring of constant 150 N/m. A driving
force F(t) = (12.0 N) cos(ωt) is applied to the mass, and the damping coefficient
b is 6.00 Ns/m. What is the amplitude (in cm) of the steady-state motion if
ω is equal to half of the natural frequency ω0 of the system?
Solution:
- Concepts:
Forced oscillations
- Reasoning:
The spring constant, driving force, and damping
coefficient for a forced harmonic oscillator are given and we are asked to
find the steady-state amplitude.
- Details of the calculation:
The equation of motion for the
harmonically driven harmonic oscillator [F(t) = F0cos(ωt)] with
damping coefficient b = 2βm is
d2x/dt2 + 2βdx/dt + ω02x
= Acosωt, with A = F0/m.
The stationary solution is x(t) = Dcos(ωt
- δ) with tanδ = 2ωβ/(ω02 - ω2) and D =
A/[(ω02 - ω2)2 + 4ω2β2]½.
[The expressions for tanδ and D are found by substituting x(t) =
Cexp(iωt) with C = Dexp(iδ) into the differential equation d2x/dt2 + 2βdx/dt
+ ω02x = Acosωt and then taking the real part of
the solution.]
In this problem
D = (F0/m)/[(ω02
- ω2)2 + (bω/m)2]½,
ω02
= k/m = 300, ω = ω0/2, ω2 = 300/4 = 75.
F0/m
= 12/0.5 = 24.
D = 24/[(300 - 75)2 + 36*75/0.25]½
= 0.0968 m = 9.7 cm is the amplitude of the steady state motion.
Problem:
A particle of mass m = 1 oscillates without friction attached to a spring
with k = 4. The motion of the particle is driven by the external force F(t) = 3
t cos(t). Find the equation of motion and solve it. Discuss the physical
meaning of the solution.
Solution:
- Concepts:
Driven oscillations
- Reasoning:
The amplitude of the driving force increases linearly with
time. For large t we expect a term x proportional to tcos(t) to dominate the solution. For small t, x = Ccos(2t +
φ), the solution to
d2x/dt2 + 4x = 0, may dominate, depending on the initial
conditions, which determine the constants C and
φ.
- Details of the calculation:
F = md2x/dt2 = -kx + F(t), d2x/dt2
+ 4x - 3t cos(t) = 0 is the equation of motion.
In complex notation: d2x/dt2 + 4x - 3t exp(it) = 0.
Try x = A(t) exp(it).
Then d2A/dt2 +2idA/dt + 3A - 3t = 0.
Let A = t + f(t). (This eliminates the term proportional
to t.)
Then d2f/dt2 + 2i(1 + df/dt) + 3f =
0.
Let f = -2i/3 + g(t). (This eliminates the constant term.)
Then d2g/dt2 + 2i dg/dt + 3g = 0.
For solutions with g not equal to zero, let g = Cexp(iat)
Then -a2 - 2a + 3 = 0, a = -1
± 2.
Most general solution:
x = (t - 2i/3 + C1exp(it) + C2 exp(-3it))exp(it)
x = (t - 2i/3)exp(it) + C1exp(2it) + C2exp(-2it)
x = texp(it) + (2/3)exp(i(t - π/2)) + C1exp(2it)
+ C2exp(-2it)
Take the real part: x = tcos(t) +
(2/3)sin(t) + Ccos(2t + φ).
The constants C and φ are determined by
the initial conditions.
Problem:
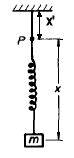
A mass m hangs in equilibrium by a spring which exerts a force F = -K(x - l),
where x is the length of the spring and l is its length when relaxed. At t
= 0 the point of support P to which the upper end of the spring is attached
begins to oscillate sinusoidally up and down with amplitude A, angular frequency
ω as shown (x' = A sin(ωt)). Set up and solve the equation of motion for
x(t).
Solution:
- Concepts:
Forced oscillations
- Reasoning:
The problem is equivalent to a forced oscillation problem
with no damping.
- Details of the calculation:
Take the upper end of the spring, P, as
the origin of the x coordinate of the mass m. Let the x-axis point
downward.
T = ½m[(d/dt)(x + x']2 = ½m[(dx/dt)2 +
(dx'/dt)2 + 2(dx/dt)(dx'/dt)].
U = -mg(x + x') + ½K(x - l)2.
L = T - U.
dL/dvx = mdx/dt + mdx'/dt. d/dt(dL/dvx)
= md2x/dt2 - mω2Asin(ωt).
dL/dx = mg -
K(x - l).
Equation of motion: md2x/dt2 - mω2Asin(ωt)
= mg - K(x - l).
d2x/dt2 + (K/m)(x - l - mg/K) = ω2Asin(ωt).
Let y = x - l - mg/K, ω02 = K/m. Then the equation of
motion becomes d2y/dt2 + ω02y =
ω2Asin(ωt).
Try a solution y = Bsin(ωt). This yields B = ω2A/(ω02
- ω2). To find the most general solution we add the homogeneous
solution y = Csin(ω0t + δ).
Most general solution: y(t) =
Csin(ω0t + δ) + [ω2A/(ω02 - ω2)]sin(ωt).
Initial conditions: mg = K(x - l), x = mg/K + l, y = 0 and dy/dt = 0 at
t = 0.
This implies δ = 0 and C = -ω3A/(ω0(ω02
- ω2)).
y(t) = -[ω3A/(ω0(ω02
- ω2))]sin(ω0t) + [ω2A/(ω02
- ω2)]sin(ωt).
x(t) = -[ω2A/(ω02
- ω2)][(ω/ω0)sin(ω0t) + sin(ωt)] + mg/K +
l.
Problem:
A simple harmonic oscillator of
mass m and resonant frequency ω is restricted to move in one dimension. Let x
denote the displacement from equilibrium. A time-dependent force F(t) of finite
duration acts on the oscillator,
(a) Show that the equation of
motion can be written as dz/dt + iωz = F(t)/m, where z = dx/dt - iωx.
(b) If the oscillator is initially at rest at equilibrium, show that the energy
transferred to the oscillator in the limit t
--> ∞ can be written as
E(t --> ∞) = (2m)-1 |∫0∞F(t)
exp(iωt) dt|2.
(c) For the force F = F0 for 0 < t < t0 and F = 0 for all
other times, where F0 is a constant, find the duration t0
of the force that transfers maximum energy to the oscillator.
Solution:
- Concepts:
The driven harmonic oscillator
- Reasoning:
The potential energy function is that of a harmonic
oscillator.
- Details of the calculation:
(a) The equation of motion for a driven simple harmonic oscillator is d2x/dt2
+ ω2x = F(t)/m.
Let z = dx/dt - iωx. Then
dz/dt = d2x/dt2 - iω(dx/dt) = d2x/dt2
- iω(z + iωx).
dz/dt + iωz = d2x/dt2 + ω2x = F(t)/m.
(b) Try a solution z =
A(t)exp(-iωt). A is a complex function.
dz/dt + iωz = (dA(t)/dt)exp(-iωt) - iωA(t)exp(-iωt) + iωA(t)exp(-iωt) = F(t)/m.
dA(t)/dt = F(t) exp(iωt)/m.
A(t) = ∫t dt'F(t') exp(iωt')/m.
We can add the solution to
the homogeneous equation z = B exp(-iωt).
So z = exp(-iωt)[B + ∫t dt'F(t') exp(iωt')/m].
Initial conditions: x(0) = 0, dx/dt|0 = 0 -->
z(0) = 0.
z(t) = exp(-iωt) ∫0t dt'F(t') exp(iωt')/m.
At any time the energy of
the system is E = ½m(d2x/dt2) + ½mω2x
= ½m|z|2.
Therefore
E(∞) = ½m|z(∞)|2 = (2m)-1|∫0∞
dt'F(t') exp(iωt')|2
is the energy transferred to the oscillator.
(c) If
F = F0 for 0 < t < t0
and F = 0 for all other times
then
E(∞) = [F02/(2m)]
|∫0t0 dt'exp(iωt')|2 = [F02/(2mω2)]
| exp(iωt0) - 1|2
= [F02/(mω2)](1
- cos(ωt0).
E(∞) has the maximum value if [2F02/(mω2)] if
ωt0 = nπ, n = odd integer.
t0 = nπ/ω, n = odd integer.


