Simple oscillations
Problem:
A particle that hangs from a spring oscillates with an angular frequency of 2
rad/s. The spring is suspended from the ceiling of an elevator car and hangs
motionless (relative to the car) as the car descends at a constant speed of 1.5
m/s. The car then suddenly stops. Neglect the mass of the spring.
(a) With what amplitude does the particle oscillate?
(b) What is the equation of motion for the particle? (Choose the upward
direction to be positive.)
Solution:
- Concepts:
Simple harmonic motion
- Reasoning:
After the elevator stops, we have a mass on a spring that moves through the
equilibrium position with a given velocity.
- Details of the calculation:
(a) When traveling in the elevator at constant speed, the total force on the
mass is zero. The force exerted by the spring is equal in magnitude to the
gravitational force on the mass, the spring has the equilibrium length of a
vertical spring. When the elevator suddenly stops, the end of the spring
attached to the ceiling stops. The mass, however has momentum, p = mv, and
therefore starts stretching the spring. It moves through the equilibrium
position of the vertical spring with its maximum velocity vmax =
1.5 m/s.
Its velocity as a function of time is v(t) = -ωAsin(ωt + Φ).
Since vmax = ωA and ω = 2/s, the amplitude of the oscillations is
A = 0.75 m.
(b) The equation of motion for the particle is d2x/dt2
= -(k/m)x = -ω2x. Its solution is
x(t) = A cos(ωt + Φ) = (0.75 m) cos((2/s)t + Φ).
If we choose the t = 0 to be the time the elevator stops and let the upward
direction be positive, then x(0) = 0, and v(0) = -1.5 m/s. We
therefore need Φ to be π/2.
Problem:
A mass of 250 g hangs on a spring and oscillates vertically with a period of
1.1 s. What mass must be added to double the period?
Solution:
- Concepts:
Simple harmonic motion
- Reasoning:
A mass-spring system is a simple harmonic oscillator.
- Details of the calculation:
For simple harmonic motion T = 2π√(m/k).
T2/T1 = 2 = √(m2/m1).
m2/m1
= 4.
m2 = 1000 g.
750 g must be added.
Problem:
Two equal masses, each of mass m, are connected by a spring
having a spring constant k. If the equilibrium separation is L0
and the spring rests on a frictionless horizontal surface, what is the frequency
of vibrations w in terms of k, m and L0?
Solution:
- Concepts:
Newton's second law
- Reasoning:
The force acting on each particle is given, F = -k(L - L0),
where L is the length of the stretched or compressed spring.
- Details of the calculation:
Place the origin of the coordinate system at the
center of mass.
For
each mass we have:
F = -k(L - L0) = md2(½ (L-L0))/dt2.
d2(L-L0)
/dt2= -(2k/m) (L - L0).
ω
= (2k/m)½.
Problem:
A certain oscillator satisfies the equation d2x/dt2 +
4x = 0. Initially the particle is at the point x = √3 when it is projected
towards the origin
with speed u = 2.
(a) Find x(t).
(b) How long does it take for the particle to first reach the origin?
Solution:
- Concepts:
Harmonic
motion
- Reasoning:
Solve the differential
equation for the given initial conditions.
- Details of the calculation:
(a) Given:
d2x/dt2 + 4x = 0, x(0) = 3, (dx/dt)(0) = -2.
x(t) = A cos(2t + φ), dx/dt = -2A sin(2t + φ)
Initial conditions: √3 = Acos(φ), 2 = 2A sin(φ)
tan(φ) = 1/√3, φ = 30 deg = π/6, A = √3/cos(π/6) = 2.
x(t) = 2 cos(2t + π/6)
(b) x(t) = 0 --> cos(2t + π/6) = 0, 2t + π/6 = π/2, t = π/6 units = 0.524
units.
Problem:
A simple pendulum is attached to the ceiling of a boxcar which accelerates at
a constant rate a. Find the equilibrium angle of the pendulum, and also the
frequency of small oscillations.
Solution:
- Concepts:
Motion in an accelerating frame, small oscillations
- Reasoning:
The boxcar is not an inertial frame.
- Details of the calculation:
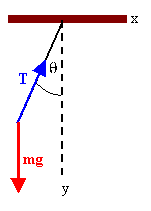
The pendulum bob is in equilibrium in the accelerating frame. It is
accelerating in an inertial frame with acceleration a = ai.
The forces on the bob are Fg = mg and
T due
to the tension in the string. We have:
Tcosθ = mg, Tsinθ = ma, tanθ
= a/g.
An observer in the boxcar experiences a fictitious force -mai. The
total force observed in the accelerating frame is therefore -m(gj
+ ai).
The magnitude of this force is mg', with g' = g/cosθ.
or g' = (g2 + a2)½. Small angular
displacements δ from the equilibrium angle θ will
result in a restoring force proportional to δ. d2δ/dt2
= -(g'/l)δ. The frequency of small oscillations is ω = (g'/l)½.
Problem:
Calculate the frequencies of oscillations of the mass m for
the two spring configurations shown in the figures. The springs have
elastic constants k1 and k2.
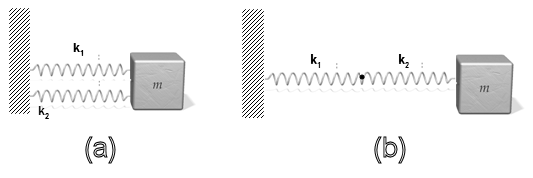
Solution:
- Concepts:
Simple
harmonic motion
- Reasoning:
We have motion in 1 dimension of a a single mass connected
to springs.
- Details of the calculation:
(a) F = - k1x - k2x
= md2x/dt2, ω2 = (k1 + k2)/m,
f = (k1 + k2))½/(2π m½).
(b) F = - k2 x2, k1x1 = k2
x2, x1 + x2 = x. x2 = k1x/(k1
+ k2).
F = - k2k1x/(k1 + k2)
= md2x/dt2, ω2 = k2k1/[m(k1
+ k2)], f = [k2k1/(k1 + k2)]½/
((2π m½).
Problem:
When the system shown in the diagram is in equilibrium, the right
spring is stretched by x1. The coefficient of static
friction between the blocks is μs. There is no friction
between the bottom block and the supporting surface. The force
constants of the springs are k and 3k (see the diagram). The blocks
have equal mass m. Find the maximum amplitude of the oscillations of
the system shown in the diagram that does not allow the top
block to slide on the bottom.
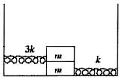
Solution:
- Concepts:
Simple harmonic motion
- Reasoning:
As long as the blocks stick together, they will execute simple harmonic
motion about an equilibrium position.
For a displacement x from the
equilibrium position, the force on each block then will obey Hooke's law, F
= -αx.
We can find the equilibrium position and α, since we know the spring
constants.
But the force on each block is also the sum of the force exerted on the
block by the spring it is attached to and the frictional force. Equating
the two expressions for the force we can find an expression for the
frictional force f, and setting if equal to its maximum value we can find
the maximum allowed amplitude for the blocks to not start sliding with
respect to each other.
- Details of the
calculation:
Let displacements to the right be positive and displacements to the left be
negative.
In equilibrium:
Force on upper block = -3kx2 + f = 0. Force on lower block = -kx1
- f = 0.
x2 = -x1/3 (Note: x1 is negative, x2
is positive.) The left spring is stretched by x1/3.
Assume the masses are stuck together. What is the equation of motion?
Let x be their displacement from equilibrium towards the right.
-kx - 3kx = 2md2x/dt2. md2x/dt2
= -2kx. x = Acosωt. ω2 = 2k/m.
The net force on each block therefore is given by F = ma = -2kx.
But we also have for the upper block F = -3k(x + x2) + f.
Therefore f = kx + 3kx2.
|fmax| = kA + 3kx2 = kA + k|x1| during one
cycle of the motion, when x = A.
For the lower block we have F = -k(x + x1) + f, therefore f = -kx
+ kx1.
|fmax| = kA + k|x1| during one cycle of the motion,
when x = -A.
If we set |fmax| = μsmg, we have Amax = μsmg/k
- |x1|.
Problem:
Three small identical coins of mass m each are connected by
two light non-conducting strings of length d each. Each coin
carries an unknown charge q. The coins are placed on a
horizontal frictionless non-conducting surface as shown (the angle between
the strings is very close to 180o). After the coins are
released, they are observed to vibrate with period T. Find the
charge q on each of the coins in terms of m, d, and T.
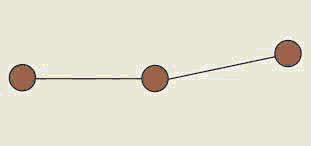
Solution:
- Concepts:
Small oscillations
- Reasoning:
The CM has to remain stationary. Choose a coordinate
system as shown in the figure below.

The system can only oscillate as indicated by the arrows in the figure.
- Details of the calculation:
Let us find the force on mass 3 located
at x = 0 as a function of its distance from the CM.
Fx = 0, Fy
= 2Ftsinθ - 2kq2sinθ/d2.
To find the tension Ft we calculate the net force, Fr,
on mass 2 along the direction making an angle
θ with the x-axis. We need Fr
= 0, since the string has a fixed length.
Fr = kq2/d2
+ kq2cosθ/(2dcosθ)2
- Ft = 0. Ft = kq2/d2 + kq2cosθ/(2dcosθ)2.
In the small angle approximation sinθ
= θ and cosθ = 1.
Ft = (5/4)kq2/d2.
Therefore Fy = ½kq2θ/d2. Fy is proportional to
θ.
The relationship between the coordinate y of mass 3 and
θ is y = -(2/3)dsinθ
= -(2/3)dθ, in the small angle
approximation. (The CM lies (2/3)dsinθ
above mass 3.)
Therefore Fy = -¾kq2y/d3.
Fy = -ay. Fy
obeys Hooke's law.
The mass oscillates with angular frequency
ω = (a/m)½
= (3kq2/(4md3))½ .
The period of
oscillation is T = 2π/ω.
T2 = 16π2md3/(3kq2) = 64π3ε0md3/(3q2). q2
= 64π3ε0md3/(3T2).
q = (64π3ε0md3/(3T2))½.
Problem:
Consider the motion of a point of mass m subjected to a potential energy
function of the form
U(x) = U0[1 - cos(x/R0)] for
πR0/2 < x < πR0/2,
where x denotes distance, and U0 and R0 are positive
constants with dimensions of energy and length, respectively.
(a) Find the position of stable equilibrium for the mass.
(b)
Show that the motion of the mass in proximity of the stable equilibrium
position is SHM.
(c) Find the period of the small oscillations.
(d) Find the period of the small oscillations for the same mass in
the potential
U(x) = -U0/[1 + (x/R0)2].
Solution:
- Concepts:
Oscillations about an equilibrium position
- Reasoning:
We are asked to find the period of small oscillations.
- Details of the calculation:
(a) The position of stable equilibrium
is x = 0.
dU/dx = (U0/R0)sin(x/R0), d2U/dx2
= (U0/R02)cos(x/R0).
dU/dx|0
= 0. d2U/dx2|0 > 0.
(b) For x << R0
we have U(x) = ½(d2U/dx2)|0x2.
This is the potential energy of a harmonic oscillator U(x) = ½kx2,
with k = d2U/dx2|0.
(c) ω2
= (1/m)(d2U/dx2)|0 = U0/(mR02).
T = 2π/ω = 2πm1/2R0/U01/2.
(d) dU/dx = (U0/R02)2x/(1 + x2/R02)2,
dU/dx|0 = 0, x = 0 is an equilibrium position.
d2U/dx2|0
= (2U0/R02) > 0.
For x << R0,
U(x) = -U0(1 - x2/R02) = -U0
+ (U0/R02)x2.
ω2 =
(2U0/(mR02)). T = 2π/ω = 21/2πm1/2R0/U01/2.
Problem:
A flexible "U-tube" with cross sectional area A is filled with a liquid of
density ρ that has no viscosity. The total length of the fluid column is L. If
one side of the U tube is suddenly lowered so that the fluid level on that side
is lowered by an amount h with respect to its initial position, when will the
heights of the two columns again be equal? (You may assume that the fluid flow
is laminar but with no sticking to the inner surface of the U tube so that all
particles in the fluid move at the same speed. Also, neglect all friction, such
as any effects of air resistance in the tube above the liquid.)
Solution:
- Concepts
The harmonic oscillator
- Reasoning:
The fluid in the tube will oscillate about its equilibrium position.
- Details of the calculation:
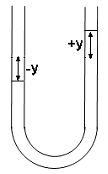
Height difference when the fluid on one side is lowered by an amount y: 2y
Magnitude of net force pushing the fluid towards its equilibrium position:
Fy = -2ρgAy
ρALd2y/dt2 = -2ρgAy, d2y/dt2 =
-(2g/L)y, y = h cos(ωt), ω = (2g/L)½, given the initial
conditions.
When ωt = π/2, t = (π/2)*(L/(2g))½, the heights of
the two columns will again be equal.






