The proper time interval
Problem:
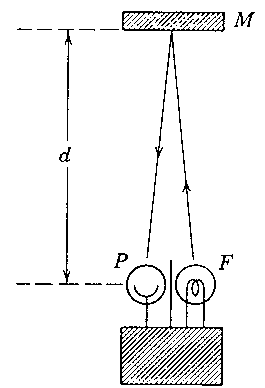
A possible clock is shown in the figure below. It consists of a flashtube F
and a photocell P shielded so that each views only the mirror M, located a
distance d away, and mounted rigidly with respect to the flashtube-photocell
assembly. The electronic innards of the box are such that, when the photocell
responds to a light flash from the mirror, the flashtube is triggered with a
negligible delay and emits a short flash towards the mirror. The clock thus
"ticks" once every (2d/c) seconds when at rest.
(a) Suppose that the clock moves with a uniform velocity v, perpendicular to
the line from PF to M, relative to an observer. Using the second postulate of
relativity, show by explicit geometrical or algebraic construction that the
observer sees the relativistic time dilatation as the clock moves by.
(b) Suppose that the clock moves with a velocity v parallel to the line from PF
to M. Verify that here, too, the clock is observed to tick more slowly, by the
same time dilatation factor.
Solution:
- Concepts:
The postulates of relativity
- Reasoning:
In vacuum, light propagates with respect to any inertial frame and in all
directions with the universal speed c. This speed is a constant of nature.
We use this postulate to calculate the time it takes a light pulse to move
from F to P.
- Details of the calculation:
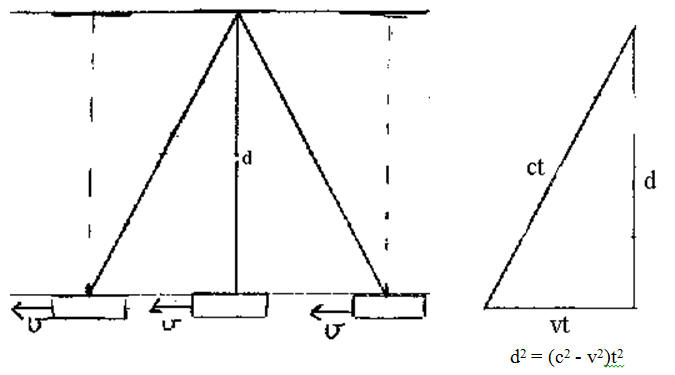
(a) The observer sees the pulse move with speed c. But the flash is not
moving a distance 2d, but a distance 2(d2 + v2(∆t2))½.
The time between ticks is
∆t = 2(d2 + v2(∆t2))½/c. ∆t =
2d/(c2 - v2)½ = γ(2d/c)
We have ∆t = γ∆τ.
(b) The observer sees the pulse move with speed c. It travels a distance d1
+ d2.
d1 = d' + vt1 = ct1, t1 = d'/(c
- v).
d2 = d' - vt2 = ct2, t2 = d'/(c
+ v).
The clock therefore ticks every t1 + t2 seconds. The
time interval between ticks is
∆t = d'/(c - v) + d'/( c+ v) = [d'(c + v) + d'(c -v )]/(c2 - v2)
= 2d'c/(c2-v2) = γ2(2d'/c).
But d' = d(1 - v2/c2)½ = d/γ, (Lorentz
contraction), therefore ∆t = γ(2d/c) = γ∆τ.
Problem:
Consider a light bulb inside a train moving with velocity v with respect to
the train station. The bulb is switched on, and its light hits the floor of the
wagon right underneath the bulb. The bulb-floor distance is h. Using only the
postulate of relativity about the speed of light, calculate the time it takes
for the light to hit the floor from the perspective of an observer at rest
inside the train and from the perspective of an observer at rest at the station
and compare those times.
Solution:
- Concepts:
Postulate: In vacuum, light propagates with respect to any inertial frame
and in all directions with the universal speed c
- Reasoning:
We use this postulate to
calculate the time it takes a light pulse to move from point 1 to point 2.
- Details of the calculation:
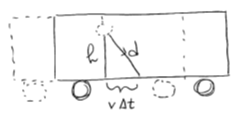
From the perspective of an observer at rest inside the train ∆tinside
= h/c.
The observer at rest at the station sees the light pulse move with speed c.
But the light pulse is not moving a distance h, but a distance (h2
+ v2(∆t'2))½.
c∆t' = (h2 + v2(∆t'2))½. ∆t'
= hd/(c2 - v2)½ = γ(h/c) = γ∆tinside,
with γ = (1 - v2/c2)-½.
We have ∆t = γ∆tinside. ∆t > ∆tinside. Moving
clocks run slow.
Problem:
The half-life of a π+ meson at rest is 2.5*10-8 s. A
beam of π+ mesons is generated at a point 15 m from a detector. Only
½ of the π+ mesons live to reach the detector. What is the speed
of the π+ mesons?
Solution:
- Concepts:
Relativistic kinematics, the proper time interval
- Reasoning:
Given the half-life ∆τ of the π+ meson in its rest frame (the
proper time) we are asked to find the relative speed v of a frame in which
the half-life is ∆t = γ∆τ = 15 m/v.
- Details of the calculation:
γ∆τ = (15 m)/v, γv = (15 m)/∆τ.
Define v0 = (15 m)/∆τ. Then
v2/(1 - v2/c2) = v02,
v2 = (v02 - v02v2/c2),
v2(1 + v02/c2) = v02.
v2 = v02/(1 + v02/c2),
v = 2.68*108 m/s = 0.894 c.
Problem:
How far will a muon (whose lifetime is 2.2 μsec in its rest
frame) move before it decays in the lab if it moving at 0.999c?
Solution:
- Concepts:
Time dilation
- Reasoning:
The proper time interval between two events (creation and
decay) is given. We are asked to find the time interval in a reference
frame moving with speed v = 0.999c with respect to the frame in which the
two events have the same space coordinates.
- Details of the calculation:
dτ = dt/γ. dt = 2.2 μsec/(1 - 0.9992)½
= 49.2 μsec
Problem:
An atomic clock is taken to the North Pole, while another
stays at the Equator. How far will they be out of synchronization after a year
has elapsed?
Solution:
- Concepts:
Relativistic kinematics, the proper time interval
- Reasoning:
The clock on the North Pole is in an inertial frame (frame 1), the clock on
the equator is in an accelerating frame (frame 2). But the clock on the
equator always moves with speed v with respect to fame 1. When the
clock in the accelerating frame measures a proper time interval of one year
between two events, the clock in the inertial frame will measure a longer
time interval between the two events.
- Details of the calculation:
[Details:
The accelerating frame is not an inertial frame. It accelerates with
respect to an imagined second frame, which is at any instant moving
alongside the accelerating frame with identical instantaneous velocity
v,
but is not accelerating. The imagined frame provides a momentary inertial
frame of reference, relative to which the acceleration is v2/r.
After a time interval
Δt measured in accelerating frame, the
clock will have velocity (v2/r)Δt in a direction
perpendicular to v with respect to the imagined frame.
The speed
with respect to frame 1 will be v' = (v2 + γ-2(v2/r)2Δt2)½
= v as Δt --> 0. So we can calculate time dilation for frames
moving in a circle with constant speed as we do for inertial frames.]
The time interval measured in frame 1 is dt =
γdt' when dt' is measured in frame 2.
Since γ is constant, t = γt'.
t' = 365*24*3600s, v = (2π*6.37*106 m)/(86400 s), γ = (1 - v2/c2)-½
≈ 1 + v2/(2c2).
t - t ' = t' v2/(2c2) = 3.8*10-5 s.
The clocks will be out of synch by 3.8*10-5 s.
Problem:
The premise of the Planet of the Apes movies and book is that hibernating
astronauts travel far into Earth's future, to a time when human civilization has
been replaced by an ape civilization. Considering only special relativity,
determine how far into Earth's future the astronauts would travel if they slept
for 120 years while traveling relative to the Earth with a speed of v = 0.9990c,
first outward from Earth and then back again.
Solution:
- Concepts:
The proper time interval
- Reasoning:
The astronauts are returning and therefore must be accelerating. The astronauts'
world line is not a straight line on a space time diagram. In the Lorentz
geometry, the proper time interval between two specified events along a curved
world line is always less than or equal to the proper time interval along a
straight world line.
- Details of the calculation:
Half the time passes on the way out and half the time passes on the return trip
in both frames.
(∆cτ)2 = (∆ct)2 - (∆x)2.
(60 ly)2 = (ctearth)2 - (vtearth)2
= (1 - v2/c2) (ctearth)2 = 2*10-3(ctearth)2
(ctearth)2 = (60 ly)2/(2*10-3).
tearth= 1342 years.
The astronauts would travel 2*1232 years = 2684 years into Earth's future.
Problem:
You wish to make a round trip from Earth in a spaceship, traveling to a
distant planet at constant speed in a straight line for exactly 6 months (as you
measure the time interval in your rest frame) spend 1 year at on the planet, and
return at the same constant speed. Assume the planet is at rest with respect to
Earth.
You wish further, on your return, to find Earth as it will be exactly 1001
years in the future as measured on Earth. At what speed v must you travel?
(Give your answer as a fraction of c.)
Solution:
- Concepts:
The proper time interval
- Reasoning:
Since you are returning, you must be accelerating. On a space time diagram you
do not have a straight world line. In the Lorentz geometry, the proper time
interval between two specified events along a curved world line is always less
than or equal to the proper time interval along a straight world line.
- Details of the calculation:
6 month = ½ year. 500 years pass on Earth during each leg of your trip. The 1
year you spend on the planet equals 1 year on Earth.
(∆cτ)2 = (∆ct)2 - (∆x)2.
(0.5 ly)2 = (500 ly) - (∆x)2. ∆x = v*500 years =
(v/c)*500 ly
(0.5 ly)2 = (500 ly) - ((v/c)*500 ly)2. 0.52/5002
= 10-6 = 1- (v/c)2.
v/c = (1 - 10-6)½ = 1 - 5*10-7.
The radius of the galaxy is 3*1020 m, measured in its own rest
frame.
(a) If the time it takes a spaceship to cross the entire galaxy is 300 years
measured in the spaceship's rest frame, what is the relative speed of spaceship
and galaxy?
(b) How much time elapses on Earth during this trip?
A space ship has a proper length of 100 m. It travels close to the
Earth's surface with a constant speed of 0.8 c. Earth observers decide to
measure the length of the ship by erecting two towers that coincide with the
ends of the ship simultaneously (in the Earth's frame) as it passes by.
(a)
How far apart do the observers on Earth build the towers?
(b) How long
do the observers on Earth say it takes for the nose of the ship to travel from
tower A to tower B?
(c) How long, according to the measurements in the
spaceship frame, does it take for the nose of the ship to travel from tower A to
tower B?
(d) As measured by passengers in the spaceship, how far apart
are the two towers?
(e) In the spaceship frame, how long does it take
a beam of light to travel from the front to the rear of the spaceship?
(f)
How much time, according to the observers on Earth, is required for a beam of
light to travel from the front to the rear of the moving spaceship?
(Give
numerical answers!)
Problem:
A space-time diagram is a plot of position versus time. It is always drawn
in an inertial frame. Consider the space-time diagram shown below.
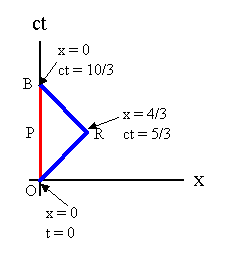
(a) Assume a particle moves along the path OPB from O to B. Describe the
motion in the inertial frame in which the space-time diagram is drawn. Find the
proper time interval (the time interval in the rest frame of the particle)
between events O and B.
(b) Assume a particle moves along the path ORB from O to B. Describe the
motion in the inertial frame in which the space-time diagram is drawn. Find the
proper time interval (the time interval in the rest frame of the particle)
between events O and B.
(c) Comment on the implication for space travel that you can deduce from your
analysis of this simple example.
(d) Draw the space-time diagram for the path ORB in the rest frame of the particle moving
from O to R. Check that the proper time intervals are correct.
Solution:
- Concepts:
The proper time interval
- Reasoning:
We are asked to find the proper time interval for different paths in a
space-time diagram.
- Details of the calculation:
(a) The particle is at rest in the inertial frame in which the space-time
diagram is drawn. The proper time interval between events O and B is (∆cτ)2
= (∆ct)2 - (∆x)2 = (∆ct)2, since ∆x = 0. ∆cτ
= 10/3.
(b) The particle moves with uniform velocity in the positive x-direction
from O to R. It accelerates briefly to change direction, and then moves
with uniform velocity in the negative x-direction from R to B.
The proper time interval between events O and R is (∆cτ)2 = (∆ct)2
- (∆x)2.
∆ct = 5/3, ∆x = 4/3, ∆cτ = 1.
Similarly, the proper time interval between events R and B is ∆cτ = 1.
The proper time interval between events O and B is ∆cτ = 2.
(c) In the Lorentz geometry, the proper time interval between two
specified events along a curved world line is always less than or equal to the
proper time interval along a straight world line. A curved world line
implies acceleration. An observer who has moved away from a place and has
accelerated to come back has aged less than an observer who has remained
stationary in an inertial frame.
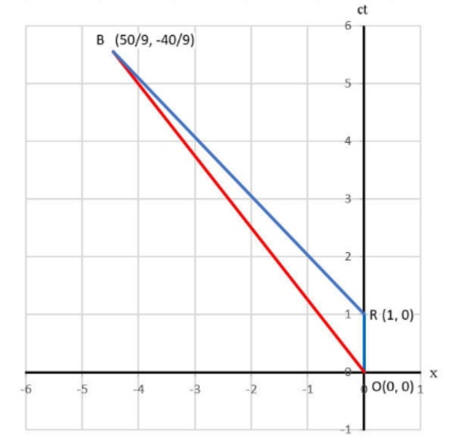 (d) Transform the coordinates of events O, R, and B from the original frame S to
the inertial frame S' that
moves with speed β = 4/5 with
respect to S in the positive
x-direction. We have γ = (1 - β2)-½ = 5/3.
(d) Transform the coordinates of events O, R, and B from the original frame S to
the inertial frame S' that
moves with speed β = 4/5 with
respect to S in the positive
x-direction. We have γ = (1 - β2)-½ = 5/3.
Event O: In S: (ct, x) = (0, 0). In S': (ct', x') = (0, 0).
Event R: In S: (ct, x) = (5/3, 4/3). In S': (ct', x') = (1, 0).
Event B: In S: (ct, x) = (10/3, 0). In S': (ct', x') = (50/9, -40/9).
Proper time interval for OB: ((50/9)2 - (40/9)2)½
= 10/3.
Proper time interval for OR: (12 - 02)½ = 1.
Proper time interval for RB: ((50/9-1)2 - (40/9)2)½
= 1.
Problem:
Twins Alice and Bob, who are 19 years old, leave the earth and travel to a
distant planet 12 light-years away. Assume that the planet and earth are at
rest with respect to each other. The twins depart at the same time on different
spaceships. Alice travels at a speed of 0.5c, and Bob travels at 0.9c.
(a) What is the difference between their ages when they meet again on earth at
the earliest possible time, and which twin is older?
(b) If instead of traveling at a constant speed of 0.5c, Alice had covered the
total distance in the same time, but on her trip to and from the planet had
accelerated and traveled 50% of the time with speed v and 50% of the time with
speed of 3v, as measured on earth, how old would she be when she meets Bob
again.
Solution:
- Concepts:
The
proper time interval in an accelerating frame
- Reasoning:
We are asked to find the proper time interval for different paths in a
space-time diagram.
- Details of the calculation:
(a) Draw a space-time diagram in the earth frame.
(∆cτ)2 = (∆ct)2 - (∆x)2.
Alice and Bob meet again when Alice returns to earth. On earth
t = (2*12 ly)/(0.5 ly/year) = 48 years have elapsed
For Alice the time 2τ has elapsed, where (∆cτ)2 = (24 ly)2
- (12 ly)2 = 432 ly2. She has aged 41.57
years.
Bob returns to earth when t = (2*12 ly)/(0.9 ly/year) = 26.67 years
have elapsed on earth.
When he returns, Bob has aged 2τ years, where (∆cτ)2 =
(13.33 ly)2 - (12 ly)2 = 33.778 ly2.
Bob has aged 11.62 years.
He now waits on earth for (48 - 26.67) years = 21.33 years to meet
Alice. When he meets Alice, he has aged 32.96 years.
When they meet Bob is 8.61 years younger than Alice.
(b) v*t/2 + 3v*t/2 = 12 ly, v*12y + 3v*12 y =12 ly, v = ¼c.
During the first half of her trip to and from the planet she covers a
distance of 0.25 ly/y * 12 y = 3 ly.
In her frame it takes her τ years, where (∆cτ)2 = (12 ly)2
- (3 ly)2 = 135 l ly2, τ = 11.82 y.
During the second half of her trip to and from the planet she covers a
distance of 0.75 ly/y * 12 y = 9 ly.
In her frame it takes her τ years, where (∆cτ)2 = (12 ly)2
- (9 ly)2 = 64 l ly2, τ = 7.94 y
When she returns to earth, she has aged 2*(11.82 y + 7.94 y) = 39.1 years.
She will be 58.1 years old.
Problem:
Assume a rocket ship leaves the earth in the year 2020. One of a set of
twins born in 2000 remains on earth, the other rides in the rocket. The rocket
ship is so constructed that it has an acceleration g in its own rest frame to
make the occupants feel at home. It accelerates in a straight line path for 5
years as measured by its own clock, decelerates at the same rate for 5 more
years, turns around, accelerates for 5 years, decelerates for 5 years, and
lands on earth. The twin in the rocket is 40 years old.
(a) What year is it on earth?
(b) How far away from earth did the rocket ship travel?
Solution:
- Concepts:
The proper time interval
- Reasoning:
We are asked to compare proper time intervals in an inertial and an
accelerating frame.
- Details of the calculation:
The accelerating rocket ship is not an inertial frame. It accelerates with
respect to an imagined second ship, which is at any instant happening to
move alongside with identical instantaneous velocity v, but is not
accelerating. The imagined ship provides a momentary inertial frame of
reference, relative to which the acceleration is g.
After a time interval dτ measured in the imagined ship, the rocket ship will
have velocity g∆τ with respect to the imagined ship.
The velocity with respect to earth will be v' = (v + gdτ)/(1 + vgdτ/c2).
v'/c = (v/c + (g/c)dτ)/(1 + vgdτ/c2).
To express this equation in terms of the boost parameter we write
v'/c = tanh(B), v/c = tanh(B1), (g/c)dτ = tanh(B2).
Then tanh(B) = (tanh(B1) + tanh(B2))/(1 + tanh(B1)tanh(B2))
= tanh(B1 + B2)
If after each time interval ∆τ we imagine a new second ship, not
accelerating, but moving with identical instantaneous velocity next to the
rocket ship, we have after n time intervals n∆τ = τ that
tanh(B) = tanh(nB2).
As dτ --> 0 we have tanh(B2) --> B2 , or B2
= (g/c)dτ.
Therefore tanh(B) = tanh((ng/c)dτ), B = (g/c)τ.
[Without using the boost parameter we can simply integrate.
We write β' = (β + (g/c)dτ)/(1 + βgdτ/c).
For an infinitesimal small time interval dτ we have
β' =
β + dβ = (β + (g/c)dτ)(1 - βgdτ/c) = β + (g/c)dτ)
- β2(g/c)dτ.
dβ = (1
- β2)(g/c)dτ, ∫0β(τ)dβ'/(1
- β'2) = tanh-1(β(τ)) = (g/c)τ.
β(τ) = tanh((g/c)τ) = tanh(B).]
γ(τ) = (1 - (v'/c)2)-½ = (1 - tanh2(B))-½
= cosh(B).
∆t = ∫τ1τ2 γ(τ)dτ, since dτ = dt/γ(τ).
∆t = ∫τ1τ2 cosh(gτ/c)dτ = (c/g)sinh(gτ/c)|τ1τ2,
since ∫ cosh(x)dx = sinh(x).
If τ1 = 0 and τ2 = 5years, then ∆t = (c/g)sinh(gτ2/c),
∆t = [(3*108 m/s)/(9.8 m/s2)]sinh[(1.75*108 s)(9.8 m/s2)/(3*108 m/s)]
= 2.6*109 s = 84 years.
(a) 2020 + 4*84 = 2356 is the year on earth.
(b) dx = v' dt = c tanh(B) dt = c tanh(B)cosh(B)dτ.
∆x = c∫τ1τ2 tanh(gτ/c)cosh(gτ/c)dτ = c∫τ1τ2
sinh(gτ/c)dτ.
If τ1 = 0 and τ2 = 5 years, then ∆x = (c2/g)(cosh(gτ2/c)
- 1).
∆x = [(3*108 m/s)2/(9.8 m/s2)](cosh(5.12) -
1) = 7.6*1017 m = 80 ly.
The ship has traveled 2*80 ly = 160 ly away from earth.
Problem:
A monochromatic particle beam consists of particles whose total energy is 100
times their rest energy. The rest lifetime of the particles is 0.10 ns. In the
laboratory, the distance between the point where the particles are generated and
the detector is 6.0 m.
(a) What is the speed of the particles?
(b)
What fraction of the generated particles reaches the detector?
Solution:
- Concepts:
Proper time, mean life
- Reasoning:
We are given the proper time interval τ (mean lifetime) in
frame 1 and the energy in frame 2. We must find the speed and mean lifetime
in frame 2.
- Details of the calculation:
(a) E = γmc2. γ = 100 = (1 -
v2/c2)-1/2, v = 0.99995 c ~ c.
(b) In
the laboratory frame the lifetime of the particles is τγ = 10 ns. If they
do not decay, they reach the detector after t = (6 m)/c = 20 ns. The number
of particles left after 20 ns is N = N0exp(t/τγ) = N0exp(-2).
The fraction reaching the detector is N/N0 = 13.5%.




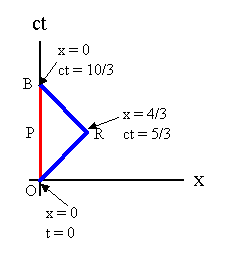
 (d) Transform the coordinates of events O, R, and B from the original frame S to
the inertial frame S' that
moves with speed β = 4/5 with
respect to S in the positive
x-direction. We have γ = (1 - β2)-½ = 5/3.
(d) Transform the coordinates of events O, R, and B from the original frame S to
the inertial frame S' that
moves with speed β = 4/5 with
respect to S in the positive
x-direction. We have γ = (1 - β2)-½ = 5/3.