The second law of thermodynamics

General

Problem:

Give two statements of the second law of thermodynamics that are not obviously identical in conceptual content but are in fact equivalent.

Solution:

• Concepts:
  The second law of thermodynamics
• Reasoning:
  We are supposed to express the second law of thermodynamics in two not obviously identical ways.
• Details of the calculation:
  (1)  Heat cannot be taken in at a certain temperature with no other change in the system and converted into work.
  (2)  The total entropy of a closed system is always increasing.

Problem:

Determine the work that can be obtained from the one cycle of the ideal Carnot machine in which the working substance is a photon gas.  The energy density of this gas is given by the u = σT⁴ and the pressure is P = (1/3)u.

Solution:

• Concepts:
  The second law of thermodynamics
• Reasoning:
  For an ideal, reversible engine Q₁/T₁ = Q₂/T₂.
• Details of the calculation:
  For a Carnot engine we have
  Q₁/T₁ = Q₂/T₂,
  W_max = (Q_high - Q_low)_reversible = Q_high - Q_highT_low/T_high = Q_high(1 - T_low/T_high).
  This is the same for all Carnot engines and does not depend on the working fluid.

Problem:

What is the efficiency of a Carnot cycle operating between the same high (T_H) and low (T_C) temperatures as the ideal gas in this circular cycle?

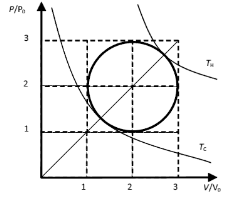
Solution:

• Concepts:
  The Carnot cycle, the ideal gas law
• Reasoning:
  The efficiency of a Carnot engine is (T_high - T_low)/T_high.
  We use the diagram (geometry) and the ideal gas law to find T_H and T_C.
• Details of the calculation:
  For the circular cycle we have  (P/P₀ - 2)² + (V/V₀ - 2)²  = 1.  (equation of a circle)
  For T_H and T_C we have P/P₀ = V/V₀.  (straight line)
  Therefore at those temperatures 2(P/P₀ - 2)² = 1, P/P₀ = 2 + 2^-½, for T_H and P/P₀ = 2 - 2^-½, for T_L.
  Using the ideal gas law, PV = nRT we have T_H = [P₀V₀/(nR)][ 2 + 2^-½]² and T_C = [P₀V₀/(nR)][ 2 - 2^-½]².
  The efficiency of a Carnot cycle operating between T_H and T_C is
  eff = (T_H - T_C)/T_H = [(2 + 2^-½)² - ( 2 - 2^-½)²]/(2 + 2^-½)²  = 77.19%

Heat engines

Problem:

An ideal heat engine is powered by two reservoirs of equal heat capacity C, which is temperature independent.  As the engine works, the reservoirs gradually equilibrate. 
(a)  Find the overall efficiency of the engine from the starting point where the reservoirs are at temperatures T₁ = 90 ^oC and T₂ = 30 ^oC to the moment of complete equilibration.
(b)  Now assume that a real heat engine is powered by the same reservoir with initial temperatures T₁ = 90 ^oC and T₂ = 30 ^oC.  Let C = 10⁵ J/^oC.  The real engine's overall efficiency is 20% of the overall efficiency of the ideal engine.  Find the change in entropy of the system once the reservoirs have equilibrated.

Problem:

A stretched rubber band contracts when heated under constant tension.  Its temperature increases when stretched adiabatically.  The equation of state for an idealized rubber band is J = αLT, where J is the tension in the rubber band, L is its length, T is the absolute temperature and α is a constant. 
For reversible processes we have for the rubber band TdS = dQ_rev = c_LdT - JdL. 
The heat capacity of the band at constant length is c_L = constant.

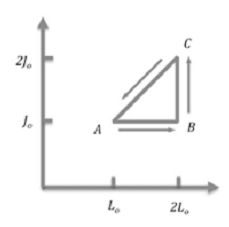
Consider a heat engine that uses a rubber band in the three-step cycle shown. 
Start with a stretched rubber band of length L₀ , tension J₀, and temperature T_A.
Take the band through a sequence of reversible processes.
A --> B:
The rubber band is stretched under constant tension J₀ to a length 2L₀ while in contact with a heat reservoir of temperature T_B. 
B --> C:
While in contact with a heat reservoir of temperature T_C the tension of the rubber band is increased from J₀ to 2J₀ at constant length 2L₀ .
C --> A:
While in contact with a heat reservoir of temperature T_A, tension and length decrease linearly from (2J₀, 2L₀) to (J₀, L₀).
(a)  Find the ratios T_B/T_A and T_C/T_A.  What is the ratio T_hot/T_cold?
(b)  Find the work done by the heat engine as it moves through one cycle A --> B --> C --> A.
(c)  During one cycle A --> B --> C --> A, how much heat is extracted from the hot reservoir and how much heat is dumped into the cold reservoir?
(d)  Find the efficiency of this rubber-band heat engine and compare it to the efficiency of a Carnot engine operating between the same temperatures.

Solution:

• Concepts:
  A simple heat engine, reversible processes
• Reasoning:
  We are asked to take a simple heat engine through one cycle.
• Details of the calculation:
  (a)  A --> B:
  J_A = J₀ =  αL₀T_A,  J_B = J₀ =  α2L₀T_B,  T_B = T_A/2,   ΔT = T_B - T_A = -T_A/2.
  B --> C:
  J_B = J₀ =  α2L₀T_B,  J_C = 2J₀ = α2L₀T_C,  T_C = 2T_B = T_A,   ΔT = T_C - T_B = T_A/2.
  C --> A:
  ΔT = 0.
  T_hot =  T_A,  T_cold =  T_B,  T_cold/T_hot = ½.
  
  (b)  A --> B:
  ΔW = -J₀L₀ = -αL₀²T_A.
  B --> C:
  ΔW = 0.
  C --> A:
  ΔW = -∫_2L0^L0JdL = -αT_A∫_2L0^L0LdL = (3/2)αL₀²T_A.
  ΔW_tot = -αL₀²T_A + (3/2)αL₀²T_A = ½αL₀²T_A.
  (c)  A --> B:
  ΔQ = -c_LT_A/2 - αL₀²T_A.
  B --> C:
  ΔQ = c_LT_A/2.
  C --> A:
  ΔQ = +(3/2)αL₀²T_A.
  ΔQ_added = (3/2)αL₀²T_A + c_LT_A/2.
  ΔQ_dumped = (c_LT_A/2 + αL₀²T_A).
  
  (d)  Efficiency = ΔW_tot/ΔQ_added = 1 /(c_L/(αL₀² ) + 3)
  The efficiency of a Carnot engine operating between T_hot = T_A and T_cold = T_B is 1 - T_B/T_A = ½.
  eff(Carnot)/eff(rubber band) = c_L/(2 αL₀² ) + 3/2.

Problem:

A Carnot heat engine has the following entropy-temperature diagram.

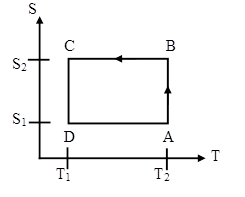
(a)  Describe the cycle.  For each segment identify the process, say whether work is done by the working system or on it and whether heat is added to the system or extracted from it.
(b)  How much work is done by the system?

Solution:

• Concepts:
  The Carnot cycle, isothermal and adiabatic processes, entropy
• Reasoning:
  The Carnot cycle consists of isothermal expansion, adiabatic expansion, isothermal compression, and adiabatic compression.
• Details of the calculation:
  (a)  A --> B:  Isothermal expansion:  The engine is in contact with a heat reservoir at temperature T₂.  The engine does work.  ΔW = ∫PΔdV.  Heat is added to the working fluid.
  B --> C:  Adiabatic expansion:  During the expansion the temperature falls to T₁.
  The engine does work.  ΔW = ∫PdV.  No heat is added or extracted from the working fluid.
  C --> D:  Isothermal compression:  The engine is in contact with a heat reservoir at temperature T₁.  Work is done on the engine.  ΔW = -∫PdV.   Heat is extracted from the working fluid.
  D --> A:   Adiabatic compression: During the compression the temperature rises to T₁.  Work is done on the engine.  ΔW = -∫PdV.  No heat is added or extracted from the working fluid.
  (b)  W = ΔQ_high - ΔQ_low = ΔS*T₂ - ΔS*T₁ = (S₂ - S₁)*(T₂ - T₁).

Problem:

The operation of a gasoline engine is (roughly) similar to the Otto cycle.  A S-V diagram is shown.

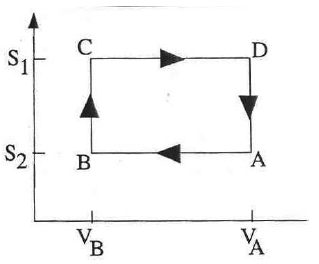
A → B:  Gas compressed adiabatically.
B → C:  Gas heated isochorically (constant volume; corresponds to combustion of gasoline).
C → D:  Gas expanded adiabatically (power stroke).
D → A:  Gas cooled isochorically.
Compute the efficiency of the Otto cycle for an ideal gas (with temperature-independent heat capacities) as a function of the compression ratio V_A/V_B, and the heat capacity of the gas, C_V .

Solution:

• Concepts:
  Heat engines
• Reasoning:
  Efficiency = net work done by the engine divided by the heat absorbed.  We use the ideal gas law and the definition of the heat capacity C_V to find these quantities.
• Details of the calculation:
  Energy conservation:  dU = dQ - PdV,  dS = dQ/T,  dU = TdS - PdV.
  For an ideal gas we have  PV = Nk_BT,  C_VdT = dU.
  Work done by the engine during one cycle:  W_tot = W_A-->B + W_C-->D = ∫_A-->BPdV + ∫_C-->DPdV.
  Heat absorbed by the engine during one cycle:  Q_in = Q_B-->C = ∫_B-->CTdS.
  Efficiency: eff = W_tot/Q_in.
  Finding W_tot:
  W_A-->B = ∫_A-->BPdV = -Nk_B∫_VB^VA (T/V)dV.
  S = S₂ = constant along the path.  We need to express T in terms of S and V.
  dS = dU/T + PdV/T = C_VdT/T + Nk_BdV/V.
  This integrates to S = C_V lnT + Nk_B lnV + constant.
  Solving for T we find:  T = α*exp(S/C_V)*V^(-Nk_B/C_V), where α is a constant.
  W_A-->B = -αNk_Bexp(S₂/C_V)∫_VB^VA V^(-1 - Nk_B/C_V))dV
  = -α exp(S₂/C_V) C_V (V_B^(-Nk_B/C_V) - V_A^(-Nk_B/C_V)).
  Similarly, W_C-->D = α exp(S₁/C_V) C_V (V_B^(-Nk_B/C_V) - V_A^(-Nk_B/C_V)).
  W_tot = α C_V ((V_B^(-Nk_B/C_V) - V_A^(-Nk_B/C_V))(exp(S₁/C_V) - exp(S₂/C_V)).
  Finding Q_in:
  Q_in = ∫_S2^S1 TdS = α*V_B^(-Nk_B/C_V)∫_S2^S1 exp(S/C_V)dS
  = α*C_V*V_B^(-Nk_B/C_V)(exp(S₁/C_V) - exp(S₂/C_V)).
  eff = 1 - (V_A/V_B)^(Nk_B/C_V).
  For a monatomic ideal gas dU = (3/2)Nk_BdT = C_VdT, Nk_B/C_V = 2/3, e = 1 - (V_A/V_B)^-2/3.

Refrigerators, Air conditioners, Heat pumps

Problem:

A refrigerator uses 10 W of electrical power when it is closed to keep the interior temperature stable.  Use reasonable estimates for any relevant temperatures to find an upper bound on the rate at which heat is entering the refrigerator due to imperfect thermal insulation.

Solution:

• Concepts:
  The second law of thermodynamics
• Reasoning:
  For a reversible process Q₁/T₁ = Q₂/T₂.  This determines the best possible coefficient of performance of the refrigerator.
• Details of the calculation:
  For a refrigerator we define the coefficient of performance COP as the ratio of the amount of heat removed at the lower temperature to the work put into the system.
  COP = Q_low/W = Q_low/(Q_high - Q_low).
  The best possible coefficient of performance is
  COP_max = Q_low/(Q_high - Q_low)_max =  Q_low/(Q_low(T_high/T_low) - Q_low) = T_low/(T_high - T_low).
  
  Let us assume that T_low = 4^oC = 277 K, and T_high = 20^oC.  Then COP_max = 277/16.
  So if the refrigerator were ideal, the heat removed per second = 10W*277/16 = 173 W.
  Upper bound on the rate at which heat is entering the refrigerator:  173 W

Problem:

An electric freezer is turned on inside a tent for a long time.  It is 0 ^oC outside the tent, +1 ^oC inside the tent, and -13 ^oC inside the freezer.  What would be the equilibrium temperature inside the tent if another freezer is turned on inside the tent?  The outside temperature remains the same.  The freezers are identical and follow the Carnot cycle.

Solution:

• Concepts:
  Thermal equilibrium, the Carnot cycle
• Reasoning:
  We have three regions:
  Region 1: The inside of the refrigerator
  Region 2:  The inside of the tent.
  Region 3:  The outside reservoir at 273 K.
  Assume region 1 and region 2 are in equilibrium with their surroundings.
  Then the heat flowing into a region per unit time must equal the heat flowing out per unit time.
• Details of the calculation:
  Region 1:  The heat flowing in is proportional to the temperature difference T₂ - T₁.
  Q₁ = b(T₂ - T₁)
  (ΔQ/Δt = -kAΔT/Δx , where k is the thermal conductivity, ΔT = (T₂ - T₁) is the difference in temperature between side 2 and side 1 of a layer of material of area A, Δx is the thickness of that layer, and ΔQ/Δt is the amount of heat that flows from side 1 to side 2 through the layer of material per unit time. )
  This heat Q₁ is removed again by the refrigerator.
  Region 2:  The heat flowing in is the heat dumped by the refrigerator.
  Q₂ = Q₁T₂/T₁ = b(T₂ - T₁)T₂/T₁
  (For the Carnot cycle Q₁/T₁ = Q₁/T2.)
  The heat flowing out is Q₃ flowing into region 3 and Q₁ flowing into region 1.  Q₃ is proportional to the temperature difference T₂ - T₃.
  Q₃ + Q₁ = a(T₂ - T₃) +  b(T₂ - T₁)
  In equilibrium Q₂ = Q₃ + Q₁.
  a(T₂ - T₃) +  b(T₂ - T₁) = b(T₂ - T₁)T₂/T₁.
  We have a/b = (T₂ - T₁)(T₂/T₁ - 1)
  With the data for the single refrigerator we can evaluate a/b.
  T₃ = 273 K, T₂ = 274 K, T₁ = 260 K, a/b = 0.7538.
  For the two refrigerators the wall area is doubled, so b --> b' = 2b, a/b' = 0.3769
  T₃ and T₁ do not change we have to solve a/b' = (T₂ - T₁)(T₂/T₁ - 1) for T₂.
  T₂ = 275.43 K = 2.43 ^oC.

Problem:

A nursery uses natural gas heating to keep the greenhouses at 30 ^oC all year.  An engineer points out that the water at the bottom of a nearby lake is at a constant temperature of 5 ^oC, and that he can build an ideal heat pump that will work at maximum possible efficiency to pump heat from this lake water into the greenhouses.  He claims that the nursery will come out ahead with his system, even though it uses electricity instead of natural gas at three times the cost per Joule.  Is he right?  Neglecting capital and maintenance costs by what factor would their energy bill change?

Solution:

• Concepts:
  The coefficient of performance for a heat pump
• Reasoning:
  The coefficient of performance for a heat pump is the ratio of the energy delivered at the higher temperature to the work put into the system, COP = Q_high/(Q_high - Q_low).  Knowing the COP, we can determine the cost of the delivered energy.
• Details of the calculation:
  The best possible coefficient of performance is
  COP_max(heat pump) = (Q_high/(Q_high - Q_low))_max = T_high/(T_high - T_low) = T_room/(T_room - T_outside)
  Here COP_max = 303/25.
  The gas heating system and the heat pump have to deliver the same amount of energy.
  For the heat pump: energy paid for = 25/303 times energy delivered
  For the gas heater: energy paid for = energy delivered
  Cost for heat pump delivery = 3*25/303 times cost for gas heater delivery
  Their new bill would be approximately ¼ their old bill.