Entropy
Problem:
An ice tray contains 500 g of water. Calculate the change in entropy of the
water as it freezes completely and slowly at 0 oC.
latent heat of fusion for water/ice = 333000 J/kg
Solution:
- Concepts:
Change in entropy: dS = dQ/T
ΔS = ∫if dS = ∫if
dQr/T
The subscript r denotes a reversible path.
- Reasoning:
We are asked calculate the change in entropy ΔS =
ΔQ/T. While the water changes phase, the temperature stays constant.
- Details of the calculation:
ΔS = ΔQ/T. ΔQ = -mL, m = mass of water,
L= latent heat of fusion = 333000 J/kg.
ΔS = -(0.5 kg)(333000J /kg)/273 K = -610 J/K.
Problem:
A cup contains 0.2 kg of tea and is heated to 90 oC.
The specific heat capacity of tea is ~ 1100 cal/(kg K). If the tea is
allowed to cool to 20 oC calculate the change in entropy (J/K).
Also calculate the entropy change in the room (Troom = 20 oC)
and show that the total change in entropy is positive.
Solution:
- Concepts:
Change in entropy:
ΔS = ∫if dS = ∫if
dQr/T
- Reasoning:
We are asked calculate the change in entropy along a
reversible path.
- Details of the calculation:
For the tea
ΔStea = ∫363K293 mcdT/T = mc
ln(293/363) = -0.2 kg * 1100 cal/(kg K) * 0.214 = -47 cal/K.
ΔStea = -47.1*4.186 J/K = -197 J/K.
For the room
ΔSroom = (0.2 kg *1100*4.186
J/K * 70 K)/(293 K) = 220 J/K.
ΔStotal = ΔStea + ΔSroom
= 23 J/K (positive)
Problem:
100 g of water at 20 oC is mixed with 100 g of
water at 80 oC. What is the net change in entropy?
Solution:
- Concepts:
Change in entropy:
ΔS = ∫if dS = ∫if
dQr/T
The subscript r denotes a reversible path.
- Reasoning:
Although this is an irreversible process, we could get the
same final result (200 g of water at 50 oC) by slowly warming the cool
water from 20 oC to 50 oC and slowly cooling the warm water
from 80 oC to 50 oC.
- Details of the calculation:
ΔS = ΔShot + ΔScold = ∫293323
dQ/T + ∫353323 dQ/T = ∫293323
mcdT/T + ∫353323 mcdT/T
= (100 g)(1 cal/( g oC))[ln(323/293) + ln(323/353)] = 0.87 cal/oC.
Problem:
The surface of the Sun is approximately at 5700 K, and the temperature of the
Earth's surface is approximately 290 K. What entropy changes occur when
1000 J of thermal energy is transferred from the Sun to the Earth?
Solution:
- Concepts:
Change in entropy:
ΔS = ∫if dS = ∫if
dQr/T
The subscript r denotes a reversible path.
- Reasoning:
We are asked calculate the change in entropy ΔS = ΔQ/T.
- Details of the calculation:
During the process the temperatures of
the sun and the earth do not change appreciably. The change in the entropy
of the sun is therefore ΔS = -1000 J/5700 K = -0.175 J/K. The change in the
entropy of the earth is ΔS = 1000J/290 K = 3.448 J/K. The entropy of the
sun-earth system increases by 3.27 J/K.
Problem:
A certain amount of water of heat capacity C is at a
temperature of 0oC. It is placed in contact with a heat reservoir at 100oC and
the two come into thermal equilibrium.
(a) What is the entropy change of
the universe?
(b) The process is now divided into two stages: first the
water is brought into contact with a heat reservoir at 50oC and comes into
thermal equilibrium; then it is placed in contact with the heat reservoir at
100oC. What is the entropy change of the universe?
(c) What is the
entropy change of the universe in the limit of infinitely many stages with
infinitely small temperature differences?
Solution:
- Concepts:
Entropy
Reasoning:
To calculate the change in entropy
of a system for a finite process, when T changes appreciably, we use ΔS = ∫ifdS
= ∫ifdQr/T, where the subscript r denotes a
reversible path. To calculate the change in entropy, we find some
reversible path that can take the system from its initial to its final state
and evaluate the integral along that path. The actual path of the system
from the initial to the final state may be very different and not
reversible. But the change in entropy depends only on the initial and final
state, not on the path.
- Details of the calculation:
(a) Change in entropy of the water:
ΔSW = ∫ifdS = ∫TiTfCdT/T
= Cln(Tf/Ti) = C*ln(373/273)
Change in entropy of
the reservoir: ΔSR = -ΔQ/(373 K) = -C*100/373
Total entropy
change: C[ln(373/273) - 100/373) = C*0.044
(b) ΔSW = C*ln(373/273)
ΔSR = -C*50/323 - C*50/373
Total entropy change: C[ln(373/273)
- C*50/323 - C*50/373) = C*0.023
(c) In this limit we have a reversible
process and ΔS = 0.
Problem:
Consider two identical blocks of material with heat capacity C, which is
temperature independent. The "hot" one is initially at temperature TH
and the "cold" one at temperature TC < TH. The
two blocks act as reservoirs for a ideal heat engine. As the engine works,
the reservoirs gradually equilibrate and reach a common temperature Tf.
(a) What is the temperature Tf?
(b) How much work does the engine do?
(c) Compute the change in entropy ΔS for each of the two blocks.
Solution:
- Concepts:
Efficiency of a heat engine, entropy
- Reasoning:
For a Carnot engine operating between Ta and Tb we
have dQa/Ta = dQb/Tb, dS = 0.
- Details of the calculation:
(a) ΔSH = ∫THTfCdT/T = Cln(Tf/TH),
ΔSC = ∫TCTfCdT/T = Cln(Tf/TC).
ΔSH + ΔSC = 0 --> ln(Tf/TH) +
ln(Tf/TC) = 0, Tf = (THTC)½.
(b) W = (QH - QC) = C(TH - Tf)
- C(Tf - TC) = C((TH - TC - 2(THTC)½).
ΔSH = ∫THTfCdT/T = Cln(Tf/TH)
= ½Cln(TC/TH).
ΔSC = ∫TCTfCdT/T = Cln(Tf/TC)
= ½Cln(TH/TC) = -ΔSH.
Problem:
An ideal heat engine is powered by two reservoirs of equal heat capacity C,
which is temperature independent. As the engine works, the reservoirs gradually
equilibrate.
(a) Find the overall efficiency of the engine from the starting point where the
reservoirs are at temperatures T1 = 90 oC and T2
= 30 oC to the moment of complete equilibration.
(b) Now assume that a real heat engine is powered by the same reservoir with
initial temperatures T1 = 90 oC and T2 = 30
oC. Let C = 105 J/oC. The real engine's overall
efficiency is 20% of the overall efficiency of the ideal engine. Find the
change in entropy of the system once the reservoirs have equilibrated.
Solution:
- Concepts:
Efficiency of a heat engine, entropy
- Reasoning:
The efficiency of a heat engine is e = W/Qhigh = (Qhigh
- Qlow)/Qhigh. For a Carnot engine operating
between Ta and Tb we have dQa/Ta
= dQb/Tb, dS = 0.
- Details of the calculation:
e = W/Qhigh = (Qhigh - Qlow)/Qhigh
= (C(T1 - Tf) - C(Tf - T2))/(C(T1
- Tf)).
ΔS1 = ∫T1TfCdT/T = Cln(Tf/T1),
ΔS2 = ∫T2TfCdT/T = Cln(Tf/T2).
ΔS1 + ΔS2 = 0 --> ln(Tf/T1) +
ln(Tf/T2) = 0, Tf = (T1T2)½
= 331.6459 K.
e = 1 - ((T1T2)½- T2))/((T1
- (T1T2)½)) = 1 - (T2/T1)½.
e = 1 - (303/363)½ = 0.0864.
(b) ΔQ = Q1 - Q2 = 0.2*Q1*(1 - (T2/T1)½),
Q2 = 0.8*Q1 + 0.2*Q1(T2/T1)½.
Q2/Q1 = C(Tf - T2)/(C(T1
- Tf)) = 0.8 + 0.2*(T2/T1)½
= 0.982725 = α.
Tf = (αT1 + T2)/(1 + α) = 332.7386 K.
ΔS1 + ΔS2 = C(ln(Tf/T1) + ln(Tf/T2))
= 658 J/K is the change in the entropy of the system.
A Carnot heat engine has the following entropy-temperature
diagram.
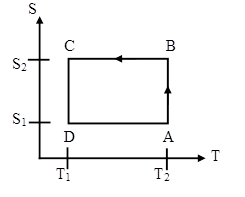
(a) Describe the cycle. For each segment identify the
process, say whether work is done by the working system or on it and whether
heat is added to the system or extracted from it.
(b) How much work is done by the system?

