Boltzmann statistics

Problem:

Neutrons are released into an evacuated cubical chamber and lowered to a very cold T = 1 mK temperature.  What is their mean height above the floor of the chamber, once their gravitational energy has reached an equilibrium distribution?  (Show work!  Derive a formula and quote a number.)

Solution:

• Concepts:
  Boltzmann distribution
• Reasoning:
  We have a macroscopic-size chamber.
• Details of the calculation:
  The probability per unit length of finding the neutron at height z is
  P(z) = P(0)exp(-mgz/(k_BT)).
  1 = P(0)∫₀^∞exp(-mgz/(k_BT))dz = P(0)k_BT/(gm),   P(0) = gm/(k_BT).
  <z> = gm/(k_BT) ∫₀^∞z exp(-mgz/(k_BT)) dz = k_BT/(gm).
  k_B = 1.380658 *10^-23 J/K.
  m_n = 1.6749286 * 10^-27 kg.
  <z> = 0.841 m.

Problem:

Consider ideal gas particles of mass m at temperature T.  What is the average speed <v> (not the rms <v²>^½ ) of the particle in terms of m, T and the Boltzmann constant k_B?

∫₀^∞x²ⁿ exp(-x²)dx = π^½ (1*3*5* ... *(2n -1))/2ⁿ⁺¹

Solution:

• Concepts:
  Boltzmann statistics
• Reasoning:
  The Boltzmann distribution gives the probability of finding particles with energy E at a given temperature T.
• Details of the calculation:
  Boltzmann statistics:  N_i/N = g_iexp(-E_i/kT)/∑_i(g_iexp(-E_i/kT))
  Here g_i is the degeneracy.
  For this problem: 
  n(v)dv/N = P(v)dv = g(v)exp(-mv²/(2kT))dv/∫₀^∞g(v')exp(-mv'²/(2kT))dv'
  = v²exp(-mv²/(2kT))dv/∫₀^∞v'²exp(-mv'²/(2kT))dv',
  since g(v) is proportional to v².
  1/∫₀^∞v'²exp(-mv'²/(2kT))dv' = (m/(2kT))^3/2(4/π^½).
  So <v> = ∫₀^∞ vP(v)dv = (m/(2kT))^3/2(4/π^½) ∫₀^∞v³exp(-mv²/(2kT))dv
  = (m/(2kT))^3/2(2/π^½) ∫₀^∞v²exp(-mv²/(2kT))dv² = (8kT/(mπ))^½.
  
  Some additional remarks:
  The Boltzmann distribution describes the distribution of energy among classical (distinguishable) particles.
  P(E) = A exp(-E/(kT))
  It can be used to evaluate the average energy per particle in the circumstance where there is no energy-dependent density of states to skew the distribution.
  To represent the probability for a given energy, it must be normalized to a probability of 1.
  ∫₀^∞ Aexp(-E/(kT))dE = 1 ==> A = 1/(kT).
  This normalized distribution function can then be used to evaluate the average energy.
  <E> = (kT)^-1∫₀^∞ Eexp(-E/(kT))dE = kT.
  This is the average energy if the energy is randomly distributed among the available energy states and there is no energy-dependent density of states.
  Note that this average energy for randomly distributed energy is not the same as the average kinetic energy.
  The average kinetic energy is found by evaluating
  <v²> = ∫₀^∞ v²P(v)dv = (m/(2kT))^3/2(4/π^½) ∫₀^∞v⁴exp(-mv²/(2kT))dv = 3kT/m.
  ½m<v²> = (3/2)kT.
  We have an energy dependent density of states.
  
  We can use E instead of v as the variable we integrate over.
  g(v)dv = g(E)dE = g(E)mvdv, g(E) = g(v)/(mv).
  Since g(v) is proportional to v², g(E) is proportional to E^½.
  We can then rewrite all the integrals in terms of E instead of v.

Problem:

Suppose a small meteorite makes a hole of area A = 1 mm² in the wall of a spaceship.  The habitable volume of the spaceship is V = 10 m³.  The temperature of the air in the spaceship is T = 27^o C and the pressure P = 105 kPa.  The molar mass of air is M = 29 g /mole.  Estimate, how much time will be available to astronauts to put on spacesuit, if the pressure should not drop by more than to 50% of its initial value.

Maxwell-Boltzmann speed distribution:  f(v) = (m/(2πkT))^3/2 4πv²exp(-mv²/(2kT)

Solution:

• Concepts:
  The Maxwell Boltzmann distribution, ideal gas law
• Reasoning:
  We need to find the escape rate R_esc = -dN/dt, then we can integrate to find N(t).  The rate with which the molecules escape from the hole
  depends on their average speed.
• Details of the calculation:
  
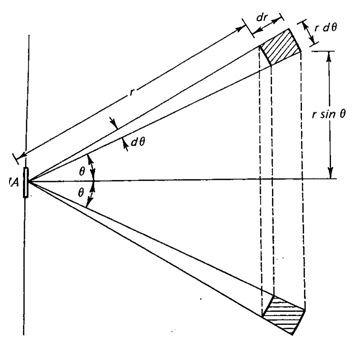
  Consider an area dA and gas molecules with speeds between v and v + dv in a ring at a distance between r and r + dr from dA.  Assume that the gas molecules travel in straight lines.
  The probability that gas molecules from the ring will reach the area dA is
  dA cosθ/(4πr²).  This is the solid angle subtended by dA at any dV in the ring.
  The number of molecules from the ring reaching dA with speeds between v and v + dv is
  nf(v)dv2πr²sinθ dr dθ dA cosθ/(4πr²) = nf(v)dv sinθ dr dθ dA cosθ/2.
  Here n = N/V is the density of the gas.
  The total number of molecules with speeds between v and v + dv reaching dA in a time interval dt comes from rings with radii between r = 0 and dr = vdt. 
  It is therefore given by 
  ∫₀^π/2 dθ nf(v)dv dA vdt sinθ cosθ/2 = ¼ n f(v) dv dA vdt.
  Integrating over all speeds we find R_esc = ¼ n dA <v>,
  where R_esc denotes rate at which gas molecules reach dA and <v> = ∫₀^∞ vf(v) dv.
  For the Maxwell Boltzmann speed distribution we find
  <v> = (8kT/(mπ))^½, where m is the mass of a gas molecule.
  R_esc = (P/kT) dA (kT/(2mπ))^½.

  R_esc  = -dN/dt is the rate at which molecules are escaping from the chamber.
  dN/dt = -(N/V) dA (kT/(2mπ))^½.
  N(t) = N₀exp(-Ct), where C = (dA/V) (kT/(2mπ))^½ = (dA/V) (RT/(2Mπ))^½
  If N/N₀ = ½, then  t = ln(2)/C.
  C = (10^-6 m²/10 m³)*[(8.314 J/K mole * 300 K)/(2* 29*10^-3 kg/mole * π)]^½ = 1.71*10^-3/s.
  t = 592 s ~ 10 minutes.

Quantized energies