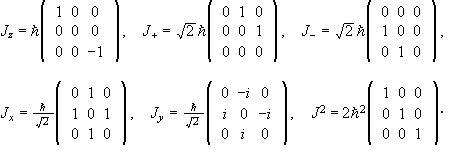
The angular momentum operators {Jx, Jy, Jz} are central to quantum theory.
States are classified according to the eigenvalues of these operators when
J is conserved by the respective Hamiltonian H.
(a) What condition(s) is (are) necessary for all eigenstates of H to be
eigenstates of J?
An eigenstate of J is usually specified by |j,mz>,
where J2|j,mz> = j(j + 1)ħ2|j,mz>
and Jz|j,mz> = mzħ|j,mz>.
(b) We can substitute Jx or Jy for Jz
in (a). However a state cannot be simultaneously an eigenstate of Jz
and Jx. Derive the commutation relation for the angular
momentum operators Jx and Jz,
(i.e. [Jx,Jz] = -iħJy)
from the definition of the linear momentum operator.
(c) Prove that it is indeed possible for a state to be simultaneously an eigenstate of
J2 = Jx2 + Jy2 +Jz2
and Jz.
Show that if any operator commutes with two of the components of an angular momentum operator, it commutes with the third.
Consider the three spin matrices
(a) Calculate the commutator of Sx and Sy.
(b) What are the possible values we can get if we measure the spin along the
x-axis?
(c) Suppose we obtain the largest value when we measure the spin along the
x-axis. If we now measure the spin along the z-axis, what are the probabilities
for the various outcomes?
Solution:

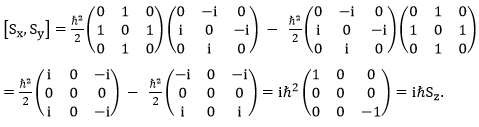
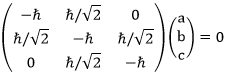 .
.Consider the vector space E(k,j) spanned by vectors with the same k and j but
different indices m.
(a) What is the dimension of this space?
(b) The space is globally invariant under the action of all components of
J.
Any component of J acting on a vector in E(k,j) yields another vector in
E(k,j). What are the matrices of Jz,
J+, and J- in E(k,j)?
(c) Write down the matrices of J2, Jz, Jx, and
Jy for j = 0, ½, and 1.
Solution:
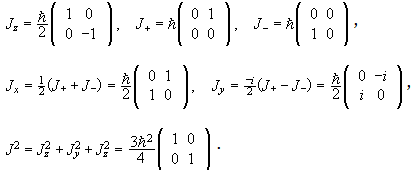
j = 1:
In the { |1>, |0>, |-1> } basis we have