Time-dependent perturbation theory

Formal

Problem:

A system makes transitions between eigenstates of H₀ under the action of the time dependent Hamiltonian H₀ + εU₀sinωt, εU₀ << H₀.  Assume that at t = 0 the system is in the state |Φ_i>.  Find an expression for the probability of transition from |Φ_i> to |Φ_f>, where |Φ_i> and |Φ_f> are eigenstates of H₀ with eigenvalues E_i and E_f.  Show that this probability is small unless E_f - E_i ~ ±ħω.
[This shows that a charged particle in an oscillating electric field with angular frequency ω will exchange energy with the field only in multiples of E = ħω.]

Solution:

• Concepts:
  Time-dependent perturbation theory
• Reasoning:
  For small perturbations time-dependent perturbation theory can be used to calculate transition probabilities.
• Details of the calculation:
  The probability of finding the system in the state |Φ_f> (f ≠ i) at time t is
  P_if(t) = (1/ħ²)|∫₀^texp(iω_fit')W_fi(t')dt'|²,
  with  ω_fi = (E_f - E_i)/ħ and W_fi(t) = <Φ_f|W(t)|Φ_i>, with W(t) = εU₀sinωt = Wsinωt and W = εU₀.
  We have to consider a sinusoidal perturbation starting at t = 0.
  ∫₀^t exp(iω_fit')W_fi(t')dt' = (W_fi/2i)∫₀^t [exp(i(ω_fi+ω)t') - exp(i(ω_fi-ω)t')]dt'
  = (W_fi/2)[(1 - exp(i(ω_fi+ω)t)/(ω_fi+ω)) - (1 - exp(i(ω_fi-ω)t)/(ω_fi-ω))].
  P_if(t) = [|W_fi|²/(4ħ²)] |(1 - exp(i(ω_fi+ω)t)/(ω_fi+ω)) - (1 - exp(i(ω_fi-ω)t)/(ω_fi-ω))|²,
  with W_fi = <Φ_f|εU₀|Φ_i>.
  The expression
  (1 - exp(i(ω_fi+ω)t)/(ω_fi+ω)) - (1 - exp(i(ω_fi-ω)t)/(ω_fi-ω))
  has an appreciable amplitude only if the denominator of one of the two terms is approximately zero, i.e.  if ω_fi = ±ω, or E_f = E_i ± ħω.  The first order effect of a perturbation that varies sinusoidally with time is to receive from or transfer to the system a quantum of energy ħω.
  If the system is initially in the ground state, then E_f > E_i, and only the second term needs to be considered.  Then
  
  P_if(t) = [|W_fi|²/(4ħ²)] sin²((ω_fi - ω)t/2)/((ω_fi - ω)/2)².
  
  Let β = ω_fi - ω, and plot sin²(βt/2)/(β/2)² = t² * sinc(βt/2) versus β.

  
  
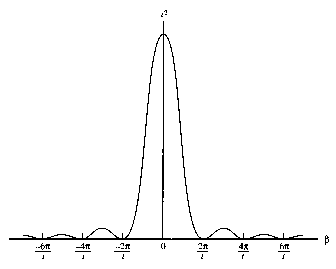
  If β = 0, i.e.  ω_fi = ω, then sin²(βt/2)/(β/2)² = t².  Therefore, if ω_fi = ω, then the probability of finding the system in the state |Φ_f>,  P_if = |W_fi|²t²/(4ħ²), increases with time proportional to t².
  For a first order approximation to be valid, we need t << ħ/|W_fi|. 
  On the other hand, to justify neglecting the first term in the above formula, we need 2ω_fi >> Δω.  2ω_fi is the difference in the positions of the peaks due to the first term and the second term in the above formula, Δω is the width of the peaks, Δω ~ 4π/t.  We therefore need t >> 1/ω_fi = 1/ω.
  Combining these two conditions we obtain 1/ω_fi << ħ/|W_fi|, or ħω_fi = (E_f - E_i) >> |W_fi|.

Problem:

A system makes transitions between eigenstates of H₀ under the action of the time dependent Hamiltonian H₀ + Wcosωt, W << H₀.  Assume that at t = 0 the system is in the state |ψ_i>.
(a)  Find an expression for the probability of transition from |ψ_i> to |ψ_f>, where |ψ_i> and |ψ_f> are eigenstates of H₀ with eigenvalues E_i and E_f.
(b)  Find an expression for the probability of transition from |ψ_i> to |ψ_f>, for a constant perturbation W.

Solution:

• Concepts:
  Time-dependent perturbation theory
• Reasoning:
  For small perturbations time-dependent perturbation theory can be used to calculate transition probabilities.
• Details of the calculation:
  (a)  The probability of finding the system in the state |ψ_f> (f ≠ i)  at time t is
  P_if(t) = (1/ħ²)|∫₀^texp(iω_fit')W_fi(t')dt'|²,
  with  ω_fi = (E_f - E_i)/ħ and W_fi(t) = <ψ_f|W(t)|ψ_i>, with W(t) = Wcosωt.
  We have to consider a sinusoidal perturbation starting at t = 0.
  ∫₀^t exp(iω_fit')W_fi(t')dt' = (W_fi/2)∫₀^t [exp(i(ω_fi+ω)t') + exp(i(ω_fi-ω)t')]dt'
  = (W_fi/2)[(1 - exp(i(ω_fi+ω)t)/(ω_fi+ω) + (1 - exp(i(ω_fi-ω)t)/(ω_fi-ω)].
  P_if(t) = [|W_fi|²/(4ħ²)] |(1 - exp(i(ω_fi+ω)t)/(ω_fi+ω)) + (1 - exp(i(ω_fi-ω)t)/(ω_fi-ω))|²,
  with W_fi = <ψ_f|W|ψ_i>.
  The expression
  (1 - exp(i(ω_fi+ω)t)/(ω_fi+ω)) + (1 - exp(i(ω_fi-ω)t)/(ω_fi-ω))
  has an appreciable amplitude only if the denominator of one of the two terms is approximately zero, i.e. if ω_fi = ±ω, or E_f = E_i ± ħω.  The first order effect of a perturbation that varies sinusoidally with time is to receive from or transfer to the system a quantum of energy ħω.
  If the system is initially in the ground state, then E_f > E_i, and only the second term needs to be considered.  Then
  P_if(t) = [|W_fi|²/(4ħ²)] sin²((ω_fi - ω)t/2)/((ω_fi - ω)/2)².
  (b) For a constant perturbation W we have
  P_if(t) = (1/ħ²)|∫₀^texp(iω_fit')W_fidt'|² = (1/ħ²)|W_fi∫₀^texp(iω_fit')dt'|²
  = (1/ħ²)|W_fi(1 - exp(iω_fit)/ω_fi)|² = [|W_fi|²/ħ²]sin²(ω_fit/2)/(ω_fi/2)².

Infinite well

Problem:

Consider a one-dimensional, infinitely deep well.  Let U(x) = 0, for 0 < x < a, and U(x) = ∞ everywhere else.  The eigenstates of H₀ = p²/(2m) + U(x) are Φ_n(x) = (2/a)^½sin(nπx/a) with eigenvalues E_n = n²π²ħ²/(2ma²).
Assume that at t = 0 you put a coin on the bottom of the well.
W(x) = W₀, a/4 < x < 3a/4 for t > 0, W(x) = 0 everywhere else, H = H₀ + W.
If at t = 0 the system is in the state Φ₃(x), what is the probability of finding it in Φ₁(x) at time t?

Solution:

• Concepts:
  The eigenfunctions of the infinite square well, time-dependent perturbation theory
• Reasoning:
  W is a small correction to H₀.  The problem governed by H₀ is already solved.
  W = 0  for  t < 0.  The probability P(E_k,t) of finding the system in the eigenstate |k> of H₀ at time t, i.e .  the probability of measuring the eigenvalue E_k, is
  P(E_k,t) = (1/ħ²)|∫₀^texp((i/ħ)(E_k-E₃)t')<Φ_k|W|Φ₃>dt'|².
  This is the result of first order time dependent perturbation theory.  P(E_k,t) is the transition probability.
  [Note: We are calculating the probability of finding the system in the ground state of the unperturbed Hamiltonian H₀, not of the perturbed Hamiltonian H.  We are calculating the probability that we find the system in the ground state after we take the coin out at time t.]
• Details of the calculation:
  P(E₁,t) = (1/ħ²)|∫₀^texp((i/ħ)(E₁-E₃)t')<Φ₁|W|Φ₃>dt'|²
  = |(<Φ₁|W|Φ₃>/ħ)∫₀^texp(iω₁₃t')dt'|²
  [∫₀^texp(iω₁₃t')dt' = (-i/ω₁₃)(exp(iω₁₃t) - 1)
  = (-i/ω₁₃)exp(iω₁₃t/2)(exp(iω₁₃t/2) - exp(-iω₁₃t/2))
  = (2/ω₁₃)exp(iω₁₃t/2)sin(ω₁₃t/2)]
  P(E₁,t) = (|<Φ₁|W|Φ₃>|²/(ħω₁₃)²)4 sin²(ω₁₃t/2).
  ω₁₃ = 8π²ħ/(2ma²).
  <Φ₁|W|Φ₃> = ∫_a/4^3a/4 dx Φ₁(x)W₀Φ₃(x)
  = (2W₀/a)∫_a/4^3a/4 dx sin(πx/a) sin(3πx/a)
  = (2W₀/π)∫_π/4^3π/4 dx sin(x) sin(3x)
  = -W₀/π.
  P(E₁,t) = (2W₀/(ħπω₁₃))²sin²(ω₁₃t/2) = (m²a⁴W₀²/(4ħ⁴π⁶))sin²(2π²ħt/(ma²)).
  P(E₁,t) oscillates with time t.
  For t > 0 the Hamiltonian is H.  At t = 0 the system is not in an eigenstate of H but in a eigenstate of H₀, an operator that does not commute with H.  The probability of finding the system in an eigenstate of an operator that does not commute with the Hamiltonian changes with time.

Problem:

Consider a particle in the ground state of a two-dimensional infinite square well.  The width of the well is L.  The ground state is not degenerate, but the excited energy levels are degenerate. 
A perturbation H' = A x sinωt with A = h²/(100 m L³) is turned on at t = 0.  Find the probability that at time t the particle will in the first excited state, for each of the degenerate states.

Solution:

• Concepts:
  The eigenfunctions of the two-dimensional infinite square well, time-dependent perturbation theory
• Reasoning:
  We have a sinusoidal perturbation starting at t = 0.  For small perturbations time-dependent perturbation theory can be used to calculate transition probabilities.
• Details of the calculation:
  The energy eigenfunctions of a particle in a two-dimensional, infinite square well are
  Φ_nx,ny(x,y) = (2/L)sin(n_xπx/L)sin(n_yπy/L)
  with eigenvalues E_nx,ny = (n_x² + n_y²)π²ħ²/(2mL²),  n_x, n_y = 1, 2, 3, ...  .
  The ground state wave function is Φ_1,1(x,y) = (2/L)sin(πx/L)sin(πy/L). 
  The first excited state wave functions are
  Φ_1,2(x,y) = (2/L)sin(πx/L)sin(2πy/L),  Φ_2,1(x,y) = (2/L)sin(2πx/L)sin(πy/L).
  We have to consider a sinusoidal perturbation H' = A x sinωt starting at t = 0.
  (A*L < E₁₁, E₁₂ = E₂₁, first order time-dependent perturbation theory is valid.)
  From first order time dependent perturbation theory we have
  P_if(t) = [|W_fi|²/(4ħ²)] sin²((ω_fi - ω)t/2)/((ω_fi - ω)/2)².
  (See problem 1.)
  Here ω_fi = (E_f - E_i)/ħ, and W(t) = Wsinωt,  W = A*x.
  For transition from the ground state to Φ_1,2 and Φ_2,1 ω_fi = 3π²ħ²/(2mL²).
  For transitions to the Φ_2,1 state we have
  W_fi = (4A/L²)∫₀^Lsin(πx/L) sin(2πx/L) x dx ∫₀^Lsin²(πy/L) dy
  = (2A/L)∫₀^L½(cos(πx/L) - cos(3πx/L)) x dx
  = (A/L)(-2L²/π² + 2L²/(9π²)) = -16AL/(9π²).
  P_if = 12.64 ħ²/(10⁴m²L⁴)sin²((ω_fi - ω)t/2)/((ω_fi - ω)/2)².
  For transitions to the Φ_1,2 state we have
  W_fi = (4A/L²)∫₀^Lsin(πy/L) sin(2πy/L) dy ∫₀^Lsin²(πx/L) x dx = 0
  P_if = 0.

Problem:

A particle of mass m and electric charge e, moving in one dimension, is confined to an interval of length a and is subject to a uniform electric field E. 
Initially it is in the eigenstate of kinetic energy with eigenvalue E_k = k²π²ħ²/(2ma²), where k is an integer. 
Find, to first order in E², the probability that after a time t its kinetic energy will be found to be E_l where k ≠ l.

Solution:

• Concepts:
  Time-dependent perturbation theory
• Reasoning:
  For small perturbations time-dependent perturbation theory can be used to calculate transition probabilities.  Here the perturbation is due to the uniform electric field.
• Details of the calculation:
  H = H₀ + W.  H₀ = T + U,  U = 0,  0 < x < a,  U = infinite elsewhere.
  Eigenfunctions of H₀:   Φ_k(x) = (2/a)^½sin(kπx/a)
  with eigenvalues E_k = k²π²ħ²/(2ma²).
  Assume the electric field points into the x-direction.
  The potential energy of a particle in this field is -eEx, with the zero of the potential energy at x = 0.
  W = -eEx.
  First order time-dependent perturbation theory yields
  P_kl(t) = (1/ħ²)|∫₀^texp(iω_lkt')W_lk(t')dt'|²,
  with with  ω_lk = (E_l - E_k)/ħ = (l² -k²)π²ħ/(2ma²)  and W_lk(t) = -eE<Φ_l|x|Φ_k>.
  W_lk(t) = -(2eE/a)∫₀^a x sin(lπx/a) sin(kπx/a) dx
  = (2eE/a)∫₀^a x ½[cos((k+l)πx/a)  - cos((k-l)πx/a)] dx
  = (eE/a)∫₀^a x [cos((k+l)πx/a) dx - (eE/a)∫₀^a x [cos((k-l)πx/a) dx
  = (eE/a)(a²/((k+l)²π²)∫₀^(k+l)π x cos(x) dx - (eE/a)(a²/((k-l)²π²)∫₀^(k-l)π x cos(x) dx.
  ∫ x cos(x) dx = cos(x) + xsin(x).
  W_lk(t) = (eE/(aπ²))[(cos((k+l)π) -1)/(k+l)² - (cos((k-l)π) -1)/(k-l)²].
  If k+l = even then (cos((k+l)π) = (cos((k-l)π) = 1, W_lk(t)  = 0.
  If k+l = odd then (cos((k+l)π) = (cos((k-l)π) = -1,
  W_lk(t)  = -2(eE/(aπ²))[((k-l)² - (k+l)²)/((k-l)²(k+l)²)] = W_lk.
  P_kl(t) = (1/ħ²)W_lk²|∫₀^texp(iω_lkt')dt'|² = (1/ħ²)W_lk²(4ħ²/(E_l - E_k)²)sin²[(E_l - E_k)t/2ħ)
  = (4W_lk²/(E_l - E_k)²)sin²[(E_l - E_k)t/2ħ).

Harmonic oscillator

Problem:

A one-dimensional harmonic oscillator is in its ground state for t < 0.
For  t > 0 it is subjected to a time-dependent but spatially uniform force in the x-direction, 
F = F₀exp(-t/τ).
(a)  Using time-dependent perturbation theory to first order, obtain the probability of finding the oscillator in its first excited state for t > 0.  Show that as t approaches infinity (with τ finite), the limit of your expression is independent of time.  Is this result reasonable, or surprising?
(b)  Can the oscillator be found in higher excited states (for t > 0 )?

Solution:

• Concepts:
  The harmonic oscillator, time dependent perturbation theory
• Reasoning:
  We are asked to find the transition probability from the ground state to an excited state for a perturbed harmonic oscillator.
• Details of the calculation:
  (a) Time dependent perturbation theory:
  P_n0(t) = (1/ħ²)|∫₀^texp(iω_n0t')W_n0(t')dt'|²
  W_n0 = <n|W(t)|0>, where W(t) = -F₀xe^-t/τ, and {|n>} are the normalized eigenstates of the harmonic oscillator Hamiltonian.
  <n|W(t)|0> = -F₀e^-t/τ<n|x|0> = CF₀e^-t/τ<n|(a + a^T)|0> = CF₀e^-t/τδ_1n.
  Here C = -(ħ/(2mω))^½.
  For the harmonic oscillator with the potential energy function ½mω²x² we have
  E_n = (n + ½)ħω.  Therefore ω_n0 = nω.
  P₁₀(t) = (1/ħ²)|∫₀^texp(iω₁₀t')W_n0(t')dt'|² = (CF₀/ħ)²|∫₀^texp(iωt')e^-t'/τdt'|²_.
  ∫₀^texp((iω-1/τ)t')dt' = [τ/(iωτ-1)][exp((iω-1/τ)t) - 1]
  |∫₀^texp(iωt') e^-t'/τdt'|² = [τ²/(ω²τ² + 1)][1 + exp(-2t/τ) + 2exp(-t/τ)cos(ωt)]
  P₁₀(t) = (CF₀/ħ)²[τ²/(ω²τ² + 1)][1 + exp(-2t/τ) - 2exp(-t/τ)cos(ωt)]
  As t -->infinity, |∫₀^texp(iωt') e^-t'/τdt'|² = [τ²/(ω²τ² + 1)].
  Since the perturbation decreases exponentially with time, we expect the probability that a transition has occurred to no longer change as t --> infinity.
  (b)  In first order time-dependent perturbation the probability of finding the oscillator in a higher excited state is zero since <n|x|0> = 0 for n > 1.

Problem:

Consider a one-dimensional oscillator in its ground state.
The unperturbed Hamiltonian is H₀ = p²/(2m) + ½mω₀²x².
At t = 0 the Hamiltonian becomes H = H₀ + H₁, where H₁ = ½mω₁²x²cosft, ω₁ << ω₀.
Calculate the transition probability to the second excited state.
Can there be a transition to any other excited state?

Note:
The stationary states of H₀ = p²/(2m) + mω₀²x²/2 are u_n(x) = N_nH_n(αx)exp(-α²x²/2)
with N_n = [α/(π^½2ⁿn!)]^½, α = (mω₀/ħ)^½  and H_n(αx) a Hermite polynomial.
Recursion relation: H_n+1(αx) = 2αxH_n(αx) - 2nH_n-1(αx).
H₀(αx) = 1,   H₁(αx) = 2αx,   H₂(αx) = 4(αx)² - 2.

Solution:

• Concepts:
  Time-dependent perturbation theory, the 1D harmonic oscillator
• Reasoning:
  H = H₀ + H₁, H₁ = W is a small, periodic perturbation.  We use time-dependent perturbation theory to calculate the probability of transitions between stationary states of H₀.
• Details of the calculation:
  P_if(t) = (1/ħ²)|∫₀^texp(iω_fit')W_fi(t')dt'|²,
  with  ω_fi = (E_f - E_i)/ħ and W_fi(t) = <ψ_f|W(t)|ψ_i>, with W(t) = Wcosft.
  We have a periodic perturbation W(t) = Wcosft starting at t = 0.
  ∫₀^t exp(iω_fit')W_fi(t')dt' = (W_fi/2)∫₀^t [exp(i(ω_fi + f)t') + exp(i(ω_fi-  f)t')]dt'
  = (iW_fi/2)[(1 - exp(i(ω_fi + f)t)/(ω_fi + f)) + (1 - exp(i(ω_fi - f)t))/(ω_fi - f))].
  P_if(t) = [|W_fi|²/(4ħ²)]|(1 - exp(i(ω_fi + f)t))/(ω_fi + f) + (1 - exp(i(ω_fi - f)t))/(ω_fi-  f))|²,
  with W_fi = <ψ_f|W|ψ_i>.
  The expression
  (1 - exp(i(ω_fi + f)t))/(ω_fi + f)) + (1 - exp(i(ω_fi - f)t))/(ω_fi - f))
  has an appreciable amplitude only if the denominator of one of the two terms is approximately zero, i.e. if ω_fi = ±f, or E_f = E_i ± ħf.  If the system is initially in the ground state, then E_f > E_i, and only the second term needs to be considered.  Then
  P_if(t) = [|W_fi|²/(4ħ²)] sin²((ω_fi - f)t/2)/((ω_fi - f)/2)².
  P₀₂(t) = [(½mω₁²)²/(4ħ²)]|<0|x²|2>|² sin²((2ω₀ - f)t/2)/((2ω₀ - f)/2)²,  since ω_fi = 2ω₀.
  P₀₂(t)  is the probability that at time t we will find the oscillator in its second excited state.
  <0|x²|2> = N₀N₂∫_-∞^∞dx H₀(αx) x² H₂(αx) exp(-α²x²)
  = N₀N₂∫_-∞^∞dx xH₀(αx) xH₂(αx) exp(-α²x²)
  = N₀N₂(½α)∫_-∞^∞dx H₁(αx) xH₂(αx) exp(-α²x²)
  = N₀N₂(1/α²)∫_-∞^∞dx H₁²(αx) exp(-α²x²)
  = [N₀N₂/(N₁²α²)] = ħ/(2^½mω₀).
  P₀₂(t) = [(½mω₁²)²/(4ħ²)](ħ²/(2m²ω₀²)) sin²((2ω₀ - f)t/2)/((2ω₀ - f)/2)²
  =  [ω₁⁴/(32ω₀²)]sin²((2ω₀ - f)t/2)/((2ω₀ - f)/2)².
  In first-order, time-dependent perturbation theory no other transitions are allowed.

Rotator

Problem:

Consider a symmetrical top, spinning about is symmetry axis with non-zero angular momentum J.  The moment of inertia of the top is I and its Hamiltonian is given by H = J²/2I.  Assume the top is perturbed by an external magnetic field B, with interaction H' = -μ∙B, where μ = GJμ_B/ħ is the magnetic moment of the top, G > 0, and μ_B is the Bohr magneton.  Assume that the top has an integer total angular momentum quantum number.
(a)  What is the energy of the top when B = 0?
(b)  What are the ground state energy and the energy of the first excited state of the spinning top when B = B₀k, B₀ > 0?
(c)  Assume that B becomes time dependent,
B(t) = B₀k, t < 0,  B(t) = B₀k + i ΔBexp(-λt), t > 0.
where ΔB << B₀ and λ > 0. 
If the top is in its first excited state for t < 0, find the probability that the top is in the ground state of part (b) for t > 0.

Solution:

• Concepts:
  The eigenstates of the angular momentum operator, time-dependent perturbation theory
• Reasoning:
  The eigenstates of the unperturbed Hamiltonian are the common eigenstates of J² and J_z.  A small perturbation is introduced and we are asked to calculate the probability or a transition between two eigenstates of the unperturbed Hamiltonian.
  
• Details of the calculation:
  (a)  H = J²/2I,  E^j = ħ²j(j+1)/2I, where j is the total angular momentum quantum number.
  (b)  H = J²/2I - (Gμ_B/ħ)J∙B  = J²/2I - ( Gμ_B/ħ)B₀J_z.
  The eigenstates of H are denoted by |j,m> (m = -j, -j+1, ..., j-1, j).
  H|jm> = (ħ²j(j+1)/2I - (Gμ_B/ħ)B₀mħ)|j,m>.
  E^jm = (ħ²j(j+1)/2I -(Gμ_B/ħ)B₀mħ).
  The ground state for a given j has m = j, the first excited state has m = j - 1.
  E₀ = ħ²j(j+1)/2I - Gμ_BB₀j,  E₁ = ħ²j(j+1)/2I - Gμ_BB₀(j-1).
  (c)  Time dependent perturbation theory yields
  P_if(t) = (1/ħ²)|∫₀^texp(iω_fit')W_fi(t')dt'|², when H = H₀ + W(t),
  with  ω_fi = (E_f - E_i)/ħ and W_fi(t) = <Φ_f|W(t)|Φ_i>.
  W(t) = -(Gμ_B/ħ)ΔBJ_xe^-λt, |Φ_i> = |j,j-1>, |Φ_f> = |j,j>
  W_fi(t') = -(Gμ_B/ħ)ΔB<j,j|J_x|j,j-1>e^-λt'.
  2J_x = J₊ + J_-,  J_±|k,j,m> = [j(j+1)-m(m±1)]^½ħ|k,j,m±1>. 
  <j,j|J_x|j,j-1> = [j(j+1)-(j-1)j]^½ħ/2 = (ħ/2)[2j]^½.
  W_fi(t') = -(Gμ_B/2)ΔB[2j]^½e^-λt'.
  ω_fi = -Gμ_BB₀/ħ.
  P_if(t) = (Gμ_BΔB/2)²2j|∫₀^texp(-iGμ_BB₀t'/ħ)e^-λt'dt'|².
  Let λ' = (iGμ_BB₀/ħ + λ).
  ∫₀^texp(-λ't')^'dt' = (1 - e^-λ't)/λ',  P_if(t) = (Gμ_BΔB/2)²2j|(1 - e^-λ't)/λ'|².

Atoms

Problem:

Assume an atom is interacting with a monochromatic (visible light) EM plane wave
E(r,t) = E₀k cos(ky - ωt).
Assume the wave functions Φ_nlm(r) of the atomic electrons are characterized by the quantum numbers n, l, and m.  Derive the selection rules for electric dipole transitions.

Solution:

• Concepts:
  Time dependent perturbation theory
• Reasoning:
  We consider the interactions of the atomic electrons with the EM wave a perturbation to the atomic Hamiltonian.
• Details of the calculation:
  The energy of an electron in the field of the plane wave to first order is W_DE = q_er∙E.
  Here W_DE = q_eE₀zcos(ωt), since we can neglect the spatial variations of visible light the plane wave over the dimensions of an atom.
  W_DE = q_eE₀zcos(ωt) is a perturbation to the atomic Hamiltonian H₀ whose eigenstates are the Φ_nlm(r).
  Time dependent perturbation theory yields
  P_if(t) = (1/ħ²)|∫₀^texp(iω_fit')W_fi(t')dt'|²,
  with  ω_fi = (E_f - E_i)/ħ and W_fi(t) = <Φ_f|W_DE(t)|Φ_i>, with W_DE(t) = q_eE₀zcos(ωt).
  P_if(t) = 0 if <Φ_f|W_DE(t)|Φ_i> = 0.  This yields the selection rules.
  
  <Φ_f|W_DE(t)|Φ_i> = q_eE₀cos(ωt)<Φ_f|z|Φ_i>. 
  Let Φ_i(r) = R_{ni li}(r)Y_{li mi}(θ,φ),  Φ_f(r) = R_{nf lf}(r)Y_{lf mf}(θ,φ).
  
  With z = r cosθ ∝ r Y₁₀(θ,φ) we have
  <Φ_f|W_DE(t)|Φ_i> ∝ ∫₀^πsinθ dθ∫₀^2πdφ Y^*_{lf mf}(θ,φ) Y₁₀(θ,φ) Y_{li mi}(θ,φ).
  The integrant is a product of three spherical harmonics.
  The integral ∫₀^πsinθ dθ∫₀^2πdφ Y_{l1 m1}(θ,φ) Y_{l2 m2}(θ,φ) Y_{l3 m3}(θ,φ) is zero unless
  (i) m₁ + m₂ + m₃ = 0,
  (ii) |l₁ - l₂| ≤ l₃ ≤ (l₁ + l₂),
  (iii) l₁ + l₂ - l₃ = even.
  Y_lm*(θ,φ) = (-1)^mY_l-m(θ,φ).
  We therefore have that <Φ_f|W_DE(t)|Φ_i> = 0 unless  m_f = m_i, l_f = l_i ± 1.  If we choose another direction for the polarization of E, i.e.  E = E₀i or E₀i, then we find  m_f = m_i ± 1, l_f = l_i ± 1.
  The dipole transition selection rules therefore are
  Δl = ±1, Δm = 0, ±1.
  These selection rules result as a consequence of the properties of the spherical harmonics.

Problem:

The electron in a hydrogen atom is in a 3d state.  Neglect the fine structure.
(a)  To what state or states (i.e. 1s etc.) can it go by radiating a photon in an allowed transition?
(b)  What is the degeneracy of the electron (include spin, but ignore spin-orbit interaction) in a 3d state?

Solution:

• Concepts:
  Selection rules Δl = 1, degeneracy of the energy level of the hydrogen atom
• Reasoning:
  Optical transitions are only "allowed" if Δl = 1.
• Details of the calculation:
  (a)  Selection rules: Δl = 1.
  An electron can only go to a 2p state in an allowed transition involving photon emission.
  (b)  l = 2 m = -2, -1, 0, 1, 2, s = + ½, - ½
  Degeneracy = 10.