Other problems with identical particles

Problem:

A particle of mass m is in a cubical well if side L, corresponding to the potential energy function
U(r) = 0 if |x|, |y| and |z| < L/2,  U(r) = ∞ otherwise.
(a)  What is its ground-state energy?
(b)  What is the energy of the first excited state?  Is this energy level degenerate or non-degenerate?  Explain!
(c)  Suppose 20 identical, non-interacting particles of mass m and spin ½ are in this well.  What is the ground state energy of this system?  Is this ground state degenerate or non-degenerate?  Explain!

Problem:

Consider a "box" that is a two dimensional square well with sides of length L x L.  Inside the well the potential is U = 0, outside the well the potential is infinite. 
(a)  Let the box contain one particle of mass M.  Determine (or write down) the general set of wave functions Φ(x,y), find the allowed energies for these states and identify the eigenvalues k_x and k_y for the particle.
(b)  Write down the three lowest energy eigenvalues and note the degeneracies, if any.
(c)  Make a plot, as a function of the eigenvalues k_x and k_y, showing the allowed states.  On this plot, consider a circle of radius k = (k_x² + k_y²)^½, with k large.  What is the area of this circle?  Approximately how many states are contained in this circle?
(d)  Now suppose that the same box contains N identical, non-interacting Fermi particles, each with mass M and spin ½.  We have N >> 1.  Find the energy of the highest occupied state, if the system is in its ground state.
(e)  For the N particle system in part d, calculate its total energy

Solution:

• Concepts:
  The two-dimensional, infinite square well, the Pauli exclusion principle.
• Reasoning:
  We are asked to find the eigenfunctions and eigenvalues of the two-dimensional, infinite square well.  When we consider a system of N non-interacting fermions in that well, we must take into account that each state can only be occupied by one spin up and one spin down particle.

• Details of the calculation:
  (a)  The eigenfunctions and eigenvalues of the 2D infinite square well are
  Φ_nm(x,y) = (2/L)sin(k_xx)sin(k_yy),  with k_x = πn/L,  k_y = πm/L,  n, m = 1, 2, ...  .
  The associated eigenvalues are
  E_nm = (n² + m²)π²ħ²/(2ML²) = (k_x² + k_y²)ħ²/(2M).

  (b)  The three lowest energy eigenvalues are
  E₁₁ = π²ħ²/(ML²),  E₁₂ = E₂₁ = 5π²ħ²/(2ML²), 
  E₂₂ = 4π²ħ²/(ML²), E₁₃ = E₃₁ = 5π²ħ²/(ML²).
  The eigenvalue 5π²ħ²/(2ML²) is degenerate. 

  (c)   k_x = πn/L,  k_y = πm/L,  ∆k_x = ∆k_y = π/L.

  

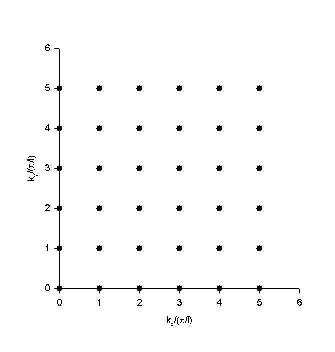
  The area of a circle in 2D k-space is  A = πk².
  The number of states in the circle is  N_states = (A/4)/(π/L)² = k²L²/(4π).
  Only positive values of k_x and k_y are allowed.
  The density of states in k-space is  n(k) = dN/dk = kL²/(2π).
  (d)  Each state can be occupied by two particles, one with spin up and one with spin down.
  If the system is in its ground state all the lowest energy levels are filled.
  The energy of the highest occupied state is E_max = ħ²k_max²/(2M),
  where N_particles = (k_max²L²/(2π) or k_max² = 2πN_particles/L².
  (e)  The number of states between k and k + dk that can be occupied is  2n(k)dk = (kL²/π)dk.
  The total energy of the system is 
  E_t = ∫₀^kmax(ħ²k'²/(2M))2n(k')dk' = ∫₀^kmax(ħ²k'²/(2M))(k'L²/π))dk'
  = (ħ²L²/(2Mπ)) ∫₀^kmax k'³dk' = (ħ²k_max⁴L²/(8Mπ)) .
  E_t = ħ²πN²_particles/(2ML²)).

Problem:

Consider an ideal 3D Fermi gas comprising N non-interacting fermions, each of mass M, in a container of volume V at T = 0
(a)  Find the Fermi energy.
(b)  Find ρ(E)dE  the number of quantum states whose energy lies in the range
E to E + dE.
(c)  Find the average energy per fermion at absolute zero by making a direct calculation of U(0)/N, where U(0) is energy at T = 0 for N fermions. Express this in terms of the Fermi energy, E_F.

Solution:

• Concepts:
  The Pauli exclusion principle, the Fermi energy
• Reasoning:
  The Fermi energy is the energy difference between the highest and lowest occupied single-particle states in a quantum system of non-interacting fermions at T = 0.
• Details of the calculation:
  (a)  The eigenfunctions and eigenvalues of the 3D infinite cubic well are
  Φ_nmp(x,y,z) = (2/L)^3/2sin(k_xx)sin(k_yy)sin(k_zz),
  with k_x = πn/L,  k_y = πm/L,  k_z = πp/L,   n, m, p = 1, 2, ...  .
  The associated eigenvalues are
  E_nmp = (n² + m² + p²)π²ħ²/(2ML²) = (k_x² + k_y² + k_z²)ħ²/(2M)
  The spacing between successive allowed values of k_i is  ∆k_x = ∆k_y = ∆k_z = π/L.  Only positive values of k_x, k_y, and k_z are allowed.
  If k is large, then the number of states with wave vectors whose magnitudes is less or equal to k is N = (1/8)(4π/3)k³/(π/L)³.
  Each state can be occupied by two particles, one with spin up and one with spin down.
  The energy of the highest occupied state is E_F = ħ²k_F²/(2M), with k_F² = (3Nπ²/V)^(2/3).
  E_F = ħ²(3Nπ²/V)^(2/3)/(2M) = ħ²(3nπ²)^(2/3)/(2M), where n is the number of particles per unit volume.
  (b)  The number of states with wave vectors whose magnitudes lie between k and k + dk is dN = (1/8)*2*4πk²dk/(π/L)³ = L³k²dk/π².  dN/dk = L³k²/π². 
  The density of states is ρ(E) = dN/dE = (dN/dk)(dk/dE).
  With E = ħ²k²/(2M) we have ρ(E) = dN/dE = L³Mk/(πħ²) = 2^½M^3/2VE^½/(π²ħ³).
  (c)  <E> = (1/N)∫₀^EFρ(E) E dE = 2^½M^3/2/(nπ²ħ³) ∫₀^EF E^3/2 dE = (2M)^3/2/(nπ²ħ³)E_F^5/2/5.
  <E> = [(2M)^3/2/(nπ²ħ³)/5]E_F*E_F^3/2.
  E_F^3/2 = ħ³(3nπ²)/(2M)^3/2.  <E> = (3/5) E_F.