The classically forbidden region

The stationary-state wave functions for a particle in an infinite square well are some of the simplest solutions of the one-dimensional Schroedinger equation.  In general, if U(x) does not go to infinity at x = 0 and x = L.  Then the wave function extends to infinity, across discontinuities in the potential energy function U(x).  The Schroedinger equation requires that the wave functions are smooth functions over the region from x = -∞ to x = +∞.  Each wave function and its derivative with respect to x (its slope) must be continuous at all positions x.  The derivative is only allowed to be discontinuous at x if U(x) = -∞ or +∞.

The time-independent Schroedinger equation

 (-ħ²/(2m))∂²ψ(x)/∂x² + U(x)ψ(x)  = Eψ(x),
or
∂²ψ(x)/∂x² + (k₁² - k₀(x)²)ψ(x) = 0,

with k₁² = 2mE/ħ² and k₀(x)² = 2mU(x)/ħ² also has solutions in regions where the total energy E = KE + U(x) is less than the potential energy U(x).  Classically a particle cannot penetrate such a region, because its kinetic energy KE in that region would be negative, which is not possible.
Let us define α(x)² = (k₀(x)² - k₁²) = (2m/ħ² )(U(x) - E).
For a classically forbidden region α² is a real, positive number.  In this region the time-independent Schroedinger equation may be written as

∂²ψ(x)/∂x² - α(x)²ψ(x) = 0.

Possible wave functions for the particle must satisfy this equation.  If in some region a is constant, independent of x, then real solutions to this equation are

ψ(x) = A exp(αx) and ψ(x) = B exp(-αx),

with A and B arbitrary constants.  The most general solution is a linear combination of these two solutions.

The finite square well

Consider a square well with walls that are not infinitely high.  Put the origin the coordinate system at the center of the well and assume

U(x) = U₀ for x < -L/2
U(x) = 0 for -L/2 < x < L/2
U(x) = U₀ for L/2 < x.

We choose a potential that is symmetric about the origin because for a symmetric 1D potential the the energy eigenfunctions are always symmetric or anti-symmetric about the origin.  We say that the eigenfunctions have even or odd parity.

How does the finite height of the walls affect the lowest lying eigenfunctions?   In the region from x = -L/2 to x = L/2 the potential energy U(x) = 0, and therefore k₀(x) = 0 and k² = k₁².  Possible wave functions for the particle still satisfy the equation ∂²ψ(x)/∂x² + k²ψ(x) = 0, and solutions are of the form ψ(x) = Acos(kx) (even) or ψ(x) = Bsin(kx) (odd).
However, since the potential does not go to infinity at the walls, the derivative ∂ψ(x)/∂x must be continuous at |x| = L/2.  ψ(x) cannot abruptly drop to zero at the walls, it must go over smoothly into a function which is a solution to Schrödinger's equation inside the wall. These solutions are ψ(x) = A exp(αx) and ψ(x) = B exp(-αx).  The wave function also cannot blow up at infinity, because we must be able to normalize it.  Therefore in the region x < -L/2 only the solution ψ(x) = A exp(αx) is acceptable and in the region L/2 < x only the solution ψ(x) = B exp(-αx) is acceptable.

To find the allowed values of E we require that the wave function and its derivative are continuous at x = L/2 and x = -L/2.

 ψ_inside(L/2) = ψ_outside((L/2),  ψ_inside(-L/2) = ψ_outside(-L/2),
 ∂ψ_inside/∂x|_L/2 = ∂ψ_outside/∂x|_L/2,  ∂ψ_inside/∂x|_-L/2 = ∂ψ_outside/∂x|_-L/2.

In the figures below we we compare the shape of the ground-state and excited-state wave functions of the infinite and the finite square well.

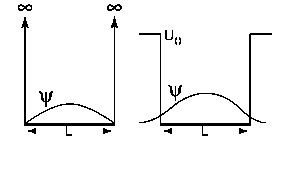
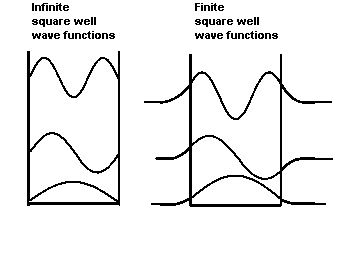
How do the energies eigenvalues compare?

Example:

• For an electron in an infinite 0.1 nm wide square well the ground state energy is 37.6 eV.

• For an electron in an finite 0.1 nm wide square well and height 1 MeV the ground state energy is 37.31 eV.

• For an electron in an finite 0.1 nm wide square well and height 1000 eV the ground state energy is 29.67 eV.

There are infinitely many bound states in an infinite square well.  There are a finite number of bound states in an finite square well.

In-class activity:  Exploring bound states in potential wells

In laboratory 4 we will solve the one-dimensional, time-independent Schroedinger equation numerically and find the energy eigenvalues of an electron trapped in wells of various shapes.

Traveling wave packets

A particle in an well does not have to be in an eigenstate of the energy operator, it can be in a superposition of eigenstates.  The probability density then is not stationary, but time-dependent.  If the well is finite, i.e. the potential does not go to infinity at the edges, then the particle can have enough energy to escape the well and not be confined.  Traveling wave packets, i.e. wave packets not confined to a well, are also not stationary states but superpositions of energy eigenstates.  They are solutions of the time-dependent Schroedinger equation

 (-ħ²/(2m))∂²ψ(x,t)/∂x² + U(x)ψ(x,t)  = iħ∂ψ(x,t)/∂t.

The applets linked below show some possible solutions of this equation for different potential energy functions U(x).  You can explore the behavior of wave packets in one-dimension for various forms of the potential energy function U(x).

Link:  Solutions to the one-dimensional Schroedinger equation for various potential energy functions