

In quantum mechanics the solutions in the classically forbidden regions are exponentially decaying solutions, and they fall to zero rapidly. But if the region in which the kinetic energy is negative is narrow, then it is possible for the exponential solution to smoothly connect two oscillating solutions on both sides of the region, and for the particle to have a finite probability of presence in that region. This leads to the phenomena of barrier penetration and tunneling.
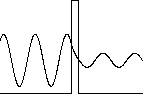
The tunneling probability strongly depends on the barrier's width and height. Most particles approaching the barrier are reflected, but a few tunnel through the barrier.
The wave function in the classically forbidden region decays as exp(-αx) as x increases from the boundary into the barrier, so for a barrier of width d the amplitude of the wave function decreases by a factor of exp(-αd). (Recall: α(x) = [(2m/ħ2 )(U(x) - E)]1/2. The probability of finding the particle on the other side of the barrier is proportional to the square of the ratio of the amplitudes and decreases as exp(-2αd).
Tunneling in two dimensions
We can consider the surface of a metal as a two-dimensional system. Electrons cannot escape, but due to “barrier penetration”, the electron density of a metal actually extends outside the surface of the metal. The distance x outside the surface of the metal at which the electron probability density drops to 1/1000 of that just inside the metal is on the order of 0.1 to 1 nanometer.
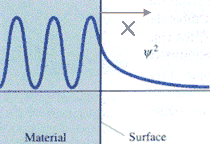
Application:
Tunneling
Microscopy
The electron probability density associated with metal atoms at a surface extends a very small distance above the surface. When a very sharp tip is brought sufficiently close to such a surface, there is a strong interaction between the electrons on the surface and that of the tip, and an electric tunneling current flows when a small voltage is applied. At a separation of a few atomic diameters, the tunneling current rapidly increases as the distance between the tip and the surface decreases. This rapid change of tunneling current with distance results in atomic resolution, if the tip is scanned over the surface to produce an image.
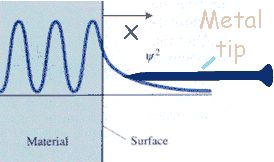 |
 Image of an actual tip. |
The tip is mounted on a piezoelectric tube, which allows tiny movements by applying a voltage at its electrodes. Thereby, the electronics of the STM system control the tip position in such a way that the tunneling current and, hence, the tip-surface distance is kept constant, while at the same time scanning a small area of the sample surface. This movement is recorded and can be displayed as an image of the surface topography. Under ideal circumstances, the individual atoms of a surface can be resolved and displayed.
This explanation is illustrated by an animated sequence.
The transmittance T is the probability that an electron will tunnel through a barrier. The transmittance T is approximately given by the simple exponential form T = exp(-2bL) with b = (2m(U0-E)/ħ2)1/2. T depends on the difference of the electron energy E and the height of the barrier U0, and on the barrier width L. For a metal (U0-E) is approximately equal to the work function of the metal.
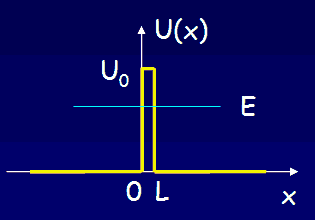
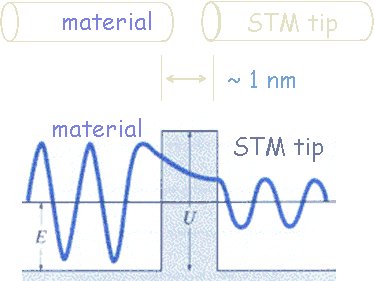
Some STM images are shown below.
Tunneling in three dimensions
Many nuclei decay to lower energy states, emitting photons or other light particles. Often the decay rate is very low. Let us consider alpha decay. The nucleus decays by emitting an alpha particle. An alpha particle is a Helium nucleus consisting of two protons and two neutrons.
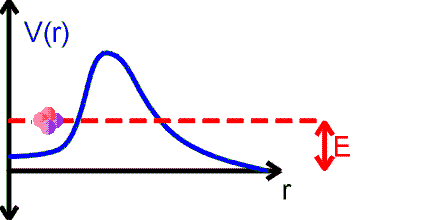
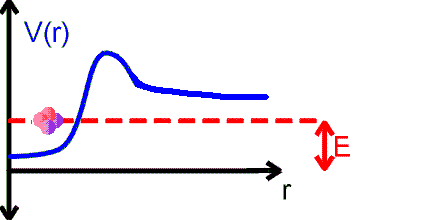
The alpha particle is trapped inside the nucleus in a potential well. But the well walls do not extend to infinity. If the shape of the well is of the form shown in the figure above, then there is a finite chance that he alpha particle can tunnel through the potential barrier. The decay of an nucleus via alpha decay takes a long time if the barrier is high and thick. Some nuclei, like lead, are considered stable but may have lifetimes greater than the age of the universe. If the barrier is not very high and narrow, alpha decay can happen very rapidly. If the shape of the barrier, however, is of the form shown in the figure below, then the alpha particle cannot tunnel through the barrier and the nucleus is stable against alpha decay.
Link: Barrier Penetration
What if quantum Mechanics determined the behavior of macroscopic objects?
 |
 |