

Pseudo-telepathy
Quantum information processing is a research area at the intersection of physics, mathematics and computer science. Pseudo-telepathy is an application of quantum information processing. Using entangled particles, two or more quantum players that are not allowed to communicate can accomplish a distributed task, which is cannot be accomplished by classical players without communicating.
Example:
A magic square is a 3 × 3 array of boxes. Each box contains either a 0 or a 1. The sum of the entries in each row is an even number (0 or 2), and the sum of the entries in each column is an odd number (1 or 3).
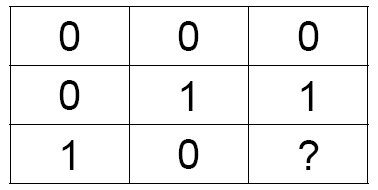
Alice and Bob are physically separated and unable to
communicate. Alice is instructed to fill in a row while Bob is instructed
to fill in a column of the magic square. They win if they put the same
number into the box at the intersection?
A classical strategy for winning every time does not exist. (Success probability: 8/9)
If Alice and Bob share two pairs of entangled particles, and each fills in the
boxes according measurements made on the two particles in their possession, then
quantum correlations can guaranty that they always will win. (Success
probability: 1)
Link: A Pseudo-Telepathy Game
Teleportation
Classical teleportation involves obtaining complete and detailed information about an object and sending that object's precise atomic configuration to another location, where the object can be reconstructed.
|
|
The problem: Quantum mechanics involves incompatible observables whose exact values cannot be known to the observer at the same time. Incompatible observables prevent the observer to obtain complete information about a system. So does quantum mechanics tell us that teleportation is impossible? |
|
Example:
The problem:
Alice has a particle in an unknown polarization state, which she cannot
measure without destroying it. She wants to teleport the particle to
Bob. Link: Teleportation |
|
Quantum Cryptography
|
|
Can Alice and Bob talk privately? The problem: Securely distributing a secret key To ensure confidentiality, data is often encrypted. The most reliable encryption techniques only use the encryption key for one session and then discard it. There exists the need for reliable and effective methods for the distribution of encryption keys. It is difficult to detect the presence of an intruder when communicating through a classical communication channel
|
|
The method:
Alice creates pairs of polarization-entangled particle, keeping one particle for herself and sending the other particle of each pair to Bob.
Alice measures the polarization of each particle she kept. She randomly chooses a vertical/horizontal (VH) or diagonal (DG) orientation for her polarizer. She records each measurement type and outcome of the measurement.
Bob measures the polarization of each particle he receives. He randomly chooses a vertical/horizontal (VH) or diagonal (DG) orientation for his polarizer. He records each measurement type and outcome of the measurement, 1 or 0.
Alice and Bob communicate over a classical channel which
type of measurement they made. They keep the data from all particle
pairs where they both chose the same measurement type. They convert
these data into a string of bits (ones and zeros) according to the outcome of the
measurement. This string of bits forms the secret key.
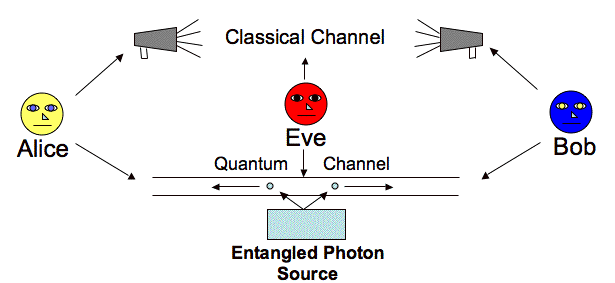
An intruder, Eve, can intercept information transmitted on a classical channel without being detected. But the only information Bob and Alice exchange on a classical channel is the type of measurements they made, which tells Eve nothing about the results of the measurement, and therefore nothing about the resulting key. If Eve can listens on the quantum channel, she will introduce errors into Bob’s final string of bits. Alice and Bob can detect these errors when they run a “key validity check”. and they will know that the security of their key has been compromised.
Link:
Quantum Cryptography