

Consider a game, in which two players play as a team against a referee. The players are physically separated and unable to communicate. We say that the players have a winning strategy if they can always win. A winning strategy can be classical (the players share only classical resources), or quantum mechanical (the players share entangled pairs of particles). A game exhibits pseudo-telepathy if a quantum winning strategy exists and a classical winning strategy does not exist.
A magic square is a 3 × 3 array of boxes. Each box contains either a 0 or a 1. The sum of the entries in each row is an even number (0 or 2), and the sum of the entries in each column is an odd number (1 or 3).
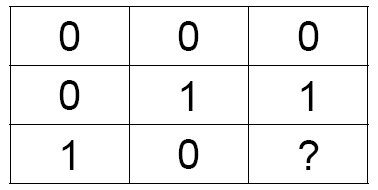
Can such a magic square exist?
This contradiction shows that a magic square does not exist.
Alice and Bob are physically separated and unable to communicate. The referee has a 3 × 3 array of boxes. The boxes are labeled by indices (i, j), i, j = 1, 2, 3.

The referee randomly picks a row (i = 1, 2, or 3) and a column (j = 1, 2, or 3). Alice only knows which row is picked and she must instruct the referee to put 0's and 1's into boxes (i, 1), (i, 2), and (i, 3) and must make sure that the entries add up to an even number. Bob only knows which column is picked and he must instruct the referee to put 0's and 1's into boxes (1, j), (2, j), and (3, j) and must make sure that the entries add up to an odd number. If Alice and Bob put the same number into box (i, j), which is the box at the intersection of Alice's row and Bob's column, then they win that round of the game.
Example of a winning round with i = j = 3
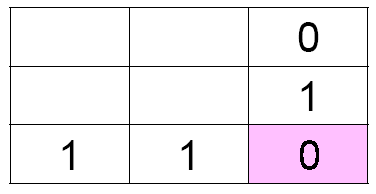
Alice and Bob need a winning strategy, so that they can win every round. Before they separate to play the game they are allowed to work on a scheme, and they are allowed to take any gadget they choose with them into their isolation cells, as long as it cannot be used to open any classical channel of communication during the game.
But a classical winning strategy does not exist. Such a strategy would correspond to the existence of a magic square. The best Alice and Bob can do is win 8 out of 9 rounds of the game on the average. A quantum strategy using just one pair of entangled particles also does not exist. But a winning quantum strategy using four entangled particles does exist.
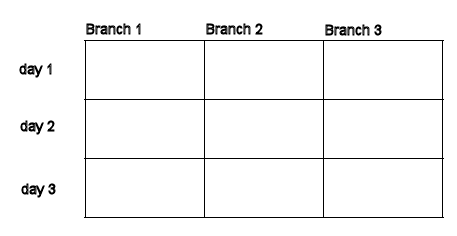
Alice and Bob are accountants. They were sent to Amsterdam to audit three bank branches. They were in Amsterdam for 3 days. Their orders were to visit at least one branch each day. If they visited more than one branch on a given day, they had to visit all three branches on that day. They could choose to visit a branch or not visit a branch. But if a branch was visited it had to be visited twice.
Management suspects that something funny was going on during their visit to Amsterdam. The managers will debrief Alice and Bob separately. Bob will be asked to provide details about one of the 3 branches. He will have to tell on which days (day 1, day 2, day 3) they visited this branch. Alice will be asked about traffic between the branches on a particular day. She will have to tell which branches (branch 1, branch 2, branch 3) they visited on that day. To avoid awkward follow-up questions they would like to develop a strategy so that, no matter which branch Bob is asked about and which day Alice is asked about, their answers agree on whether they visited this branch on that day. A classical strategy does not exist. If they used a 0 for "visited" and a 1 for "not visited" their strategy would have to amount to constructing a magic square. But a magic square does not exist.
Look at the array below. Each day Alice and Bob visited either one or three branches. So we have either one 0 and two 1's or three 0's in each row. The sum of each row is even. Each branch was visited either zero or two times. So we have either three 1's or two 0's and one 1 in each column. The sum of each column is odd. We have a magic square. The best classical strategy has only a success probability of 8/9.
Reference:
Am. J. Phys. 75 (8), August 2007
(Download using a computer connected to the UT network.)
Review: one spin 1/2 particle
Consider a physical property of a particle that, when measured, always yields one of two distinct results. An example is the z-component of the spin of an electron, Sz. We always measure ħ/2 or -ħ/2. After the measurement the electron is in an eigenstate of the Sz operator. We previously denoted the eigenstates of the Sz operator by |+> and |->.
In quantum mechanics, we encounter incompatible observables which cannot be measured simultaneously. We can measure the z-component of an electron's spin, obtain ħ/2, and know that the electron is in the |+> state. But if we then measure the x-component of the spin of the electron we lose the information we had about the z-component. The eigenstates of the Sx operator are a linear combination of the eigenstates of the Sz operator and vice versa. We can write
|+>x = 2-1/2(|+> + |->), |->x
= 2-1/2(|+> - |->),
or
|+> = 2-1/2(|+>x + |->x), |->
= 2-1/2(|+>x - |->x),
i.e. we can express the eigenstates of one of the incompatible operators in terms of the eigenstates of the other incompatible operator, but we cannot find common eigenstates. If two observables are compatible and can be measured simultaneously, then we can find common eigenstates.
Two spin 1/2 particles
If we have two spin 1/2 particles, we can measure the observable Sz = S1z + S2z. The eigenstates of this observable are denoted by |++>, |+->, |-+>, and |--> and the eigenvalues are ħ, 0, 0, and -ħ respectively. Sz measures the sum of the z-components of the spins of the two electrons. Sz is a two-particle observable.
We will now consider sets of two-particle observables which are incompatible with Sz of the two-particle system, but which have common eigenstates and can be measured simultaneously. The operators corresponding to these observables are product operators, the first one-particle operator measures a property of particle 1 and the second one-particle operator measures a property of particle 2. The identity operator I just measures if the particle exists.
The two-particle observables we are considering are listed in the table below.

The three observables in each row are compatible and have common eigenstates. They can be measured simultaneously, and the result of each measurement is either a positive number (with units) or it is a negative number (with units). If the result is positive, we flag it with the number 1, and if it is negative, we flag it with the number 0. The eigenstates of these operators can all be expressed as linear combinations of the eigenstates of Sz,
a|++> + b|+-> + c|-+> + d|-->,
with the expansion coefficients a, b, c, d being either 1, 0, or
-1. We invent a shortcut notation, and list a state a|++>
+ b|+-> + c|-+> +
d|--> as
![]() .
.
The three observables in each column are compatible and have common eigenstates. They can be measured simultaneously, and the result of each measurement is either a positive number (with units) or it is a negative number (with units). If the result is positive, we flag it with the number 1, and if it is negative, we flag it with the number 0.
Compatible observables can be measured simultaneously or in succession, and measuring one of them will not alter the information we already have about the others. So if we know the value of the observable in cell (i, j) from a measurement, then measuring all the observables in row i will not change this information, and measuring all the observables in column j will not change this information. Measuring row i or column j, we will get the same value for cell (i, j).
Assume that before Alice and Bob separate, they create a collection of spin entangled particles. A source emits four spin 1/2 particles with particles 1 and 2 and particles 3 and 4 being in Bell (entangled) states (|+>1|+>2 + |->1|->2) * (|+>3|+>4 + |->3|->4). Particles 1 and 3 go to Alice and particles 2 and 4 go to Bob. Multiplying, and labeling the particles that go to Alice with the subscript A and the particles that go to Bob with the subscript B the entangled state can be written as
|++>A|++>B + |+->A|+->B + |-+>A|-+>B + |-->A|-->B.
This state is maximally entangled. If Alice, for example measures the z-component of the spin of her two particles, she will find the particles in the states |++>, |+->, |-+>, or |--> with equal probability. But if she finds her two particles in the state |++>, she knows that Bob's particles are in the same state. No matter what she is measuring and what the result of her measurement is, the measurement always leaves her particles and Bob's particles in the same state.
Alice and Bob each use a device, called an entangulator, which can store particles and perform measurements on them. Alice stores her two particles in her entangulator, and Bob stores his two particles in his entangulators. The two entangulators are not connected in any way, and cannot communicate with each other. Each entangulator has three buttons. If Alice pushes button i (i = 1, 2, 3), then the entangulator will measure the 3 two-particle observables in row i and output a string of 0's and 1's for Alice to put into the cells (i, 1), (i, 2), and (i, 3) of row i. If Bob pushes button j (j = 1, 2, 3), then the entangulator will measure the 3 two-particle observables in column j and output a string of 0's and 1's for Bob to put into the cells (1, j), (2, j), and (3, j) of column j.
Alice's entangulator measures the observables in a selected row and Bob's entangulator measures the observables in a selected column of the table below. The buttons on the entangulators determine which row and which column will be selected.

We have already shown that if a row and a column or a column and a row are measured in succession by the same observer, the observer always obtains the same result for the cell at the intersection of the row and column. But the particles in Alice's and Bob's entangulators are entangled. So it does not matter that the second measurement is made by the other observer. After the first measurement, the particles of the two observers are in exactly the same state, and since this state is an eigenstate of the observable in the cell at the intersection, a measurement of this observable will produce exactly the same result, no matter which set of particles is used.
If the entangulators are filled with enough entangled particles for many rounds of play, then they provide the winning strategy for the magic square game. The referee randomly picks two numbers, i and j, between 1 and 3. He asks Alice to fill in row i and Bob to fill in column j. Alice pushes button i on her entangulator and receives a string of three numbers, which she tells the referee to enter into cells (i, 1), (i, 2), and (i, 3). Bob pushes button j on his entangulator and receives a string of three numbers, which he tells the referee to enters into cells (1, j), (2, j), and (3, j). Bob and Alice will always enter the same number into cell (i, j), and therefore will win every round of the game.