

Review:
Quantum Mechanics divides the world into two parts, commonly called the system and the observer. The system is the part of the world that is being modeled. The rest of the world is the observer. An interaction between the observer and the system is called a measurement. Properties of the system that can be measured are called observables. The initial information the observer has about the system comes from a set of measurements. The state of the system represents this information. Quantum mechanics predicts how the state of the system evolves and therefore how the information the observer has about the system evolves with time. Some information is retained, and some is lost. The evolution of the state is deterministic. Measurements at a later time provide new information, and therefore the state of the system, in general, changes after the measurements.
A measurement of an observable yields a value, called an eigenvalue of the observable. Many observables have quantized eigenvalues, i.e. the measurement can only yield one of a discrete set of values. Right after the measurement, the state of the system is an eigenstate of the observable, which means that the value of the observable is exactly known.
A state can be a simultaneous eigenstate of several observable, which means that the observer can exactly know the value of several properties of the system at the same time and make exact predictions about the outcome of measurements of those properties. But there are also incompatible observables whose exact values cannot be known to the observer at the same time. A state cannot be a simultaneous eigenstate of incompatible observables. If it is in an eigenstate of one of the incompatible observables and the value of this observable is known, then quantum mechanics gives only the probabilities for measuring each of the different eigenvalues of the other incompatible observables. The eigenstate of the first observable is a superposition of eigenstates of any of the other incompatible observables. The outcome of a measurement of any of the other incompatible observables is uncertain. A measurement of one of the other incompatible observables changes the state of the system to one of its eigenstates and destroys the information about the value of the first observable.
Example: A quantum eraser
Eigenstates of the total energy operator
or the Hamiltonian are stationary states.
Probabilities for measuring the different eigenvalues of observables that are
compatible with the Hamiltonian and whose eigenstates are therefore stationary
states do not change with time.
Probabilities for measuring the different eigenvalues of observables that are
incompatible with the Hamiltonian and whose eigenstates are therefore not
stationary states do change with time.
A simple quantum-mechanical system is a two-state system. Every observable of this system has only two eigenvalues and two associated eigenstates. Two-state systems are often used to demonstrate some of the essential, but counterintuitive features of quantum mechanics, because there mathematical description is the least complicated. An example of a two-state system is photon polarization. Another example of a two-state quantum system is spin polarization of a spin 1/2 particle.
Electrons have an intrinsic property called spin. Spin is intrinsic angular momentum. It is quantized. The spin angular momentum of an electron, measured along any particular direction, can only take on the values ħ/2 or -ħ/2. There are only two possible outcomes for the measurement. The spin operator Su associated with a measurement of the component of the spin along any axis u defined by two angles (θ, φ)u has only two eigenstates. We have an example of a two-state system.
Let us assume that the eigenstates of all spin operators are stationary states, i.e. that the operators are compatible with the Hamiltonian. But measurements of the spin angular momentum of an electron along different axes are incompatible measurements. If we measure an electron's spin component Sz and obtain the values ħ/2, we know that the electron is in the |+> state. If we subsequently measure the electron's spin component along another axis, we lose the information obtained from the first measurement, independent of the outcome of the second measurement. After having made this second measurement, we can only give the probabilities for obtaining the values ħ/2 or -ħ/2 if we would measure Sz again.
Assume a beam of electrons is emerging from a spin filter with its "up" axis pointing into the z-direction, as shown below.

The emerging electrons all are in the |+> state, and they are traveling along the y-axis. Assume that the electrons then enter another spin filter whose "up" axis can point along one of three different directions. What fraction of the electrons will pass through the second filter?

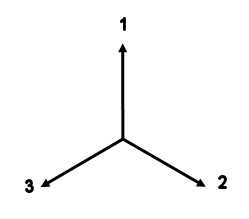
Quantum mechanics tells us that if the angle between the "up" axes of two consecutive spin filters is θ, then the probability that an electron that passed through the first filter will also pass through the second filter is cos2(θ/2).
If the "up" axis of the second analyzer points along direction
1, 100% of the electrons will pass through the analyzer.
If the "up" axis of the second analyzer points along direction 2, cos2(θ/2)
= cos2(60o) = 1/4 (25%) of the electrons will pass through
the analyzer.
If the "up" axis of the second analyzer points along direction 3, cos2(θ/2)
= cos2(60o) = 1/4 (25%) of the electrons will pass through
the analyzer.
Correlations
Assume that a radioactive substance emits a pair of electrons in each decay and that the two electrons are emitted in opposite directions. Assume that angular momentum conservation dictates that the total spin of the two electrons is zero. The magnitude of the total spin is zero and the component of the total spin measured along any axis is zero. The two electrons are entangled. Entanglement means as far as spin is concerned neither particle has properties of its own, they only have common properties. The state of of this total spin = 0, the two electron system may be written as
|ψ(1,2)> = 2-1/2(|+>1|->2 - |->1|+>2)
A combination of two single- particle, two-state systems yields a four-state system. Every observable of this combined system has only four eigenvalues and four associated eigenstates. The combined system has compatible and incompatible observables. Having information about some of the properties of the combined system (obtained from measurements) is incompatible with having information about the properties of the individual particles. Knowing that the magnitude of the total spin is zero prevents us from knowing anything about the spin directions of the individual electrons. The entangled two-particle state is a superposition of states with known spin directions for the individual particles.
With a combination of spin filters as shown below, we will try to measure the projections of the spins of both particles along various axes and look for correlations.
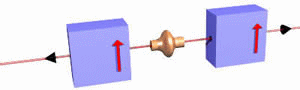
We do not know if the electrons moving to the right or left will pass either filter. But we know that if we look at correlations, we will find that if an electron does pass through the right filter, then its companion electron does not pass through the left filters. Similarly, if the electron does not pass through the right filter, then its companion electron does pass through the left filters. Each radioactive decay has a total spin of zero. If one electron is spin up its companion electron is spin down. If we change the orientation of one of the filters by 180o with respect to the other filter, we will observe that if a particular electron passes through its filter, then its companion electron will also pass through its filter. Similarly, if a particular electron does not pass through its filter, neither does its companion electron. These outcomes are independent of the absolute orientation or separation of the filters.
How do these results for entangled electrons differ from results for electrons that are not entangled?
Assume we have a source that independently emits two electrons. We know that one of them has Sz = ħ/2, and the other has Sz = -ħ/2. But we have incomplete information and do not know which electron is the spin-up electron.
These electrons are not entangled. We have no knowledge tat, in principle, prevents us from knowing their individual spin states. What correlations will we measure when we use the apparatus described above and send one electron to the right and the other one to the left?

In the orientation shown in the figure above, the result
will be the same as for the entangled electrons. The correlation will be
zero. But if we change the orientation of the filter apparatus as a whole
while keeping the source fixed, the correlation will change. If we, for
example, rotate the apparatus by 90o, the correlation will be
50%.
For an entangled state the correlation will always be zero, no matter how
the apparatus as a whole is oriented in space and no matter how
far away from each other the two filters are located. If one observer
measures the spin to be "up" along an arbitrary direction, then the other
observer will measure it down along the same direction. Some properties of
the two entangled electrons are inextricably linked to each other, even if
the electrons are located on opposite sides of the galaxy. In this sense,
quantum mechanics is said to be "nonlocal".
Now let us consider the following experimental setup.
A source of entangled electrons is placed between two spin filters, for which the "up" axis can be switched to point along directions 1, 2, or 3 as shown in the figure below. The filters are mounted in boxes. The box which contains the right filter is rotated by 180o with respect to the box which contains the left filter. The source and the two filters are not connected in any way and can be separated by very large distances.
| A | B | |
 |
 |
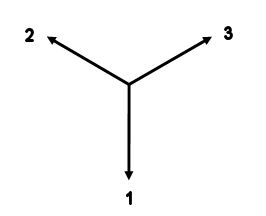 |
Each filter is rigged in such a way, that, if an electron passes the filter, a light on the box flashes green, and if an electron hits the beam stop and does not pass, a light on the box flashes red. There are two observers, Alice (A) and Bob (B). Alice can choose the orientation of filter A and can observe the flashing light on box A. Bob can choose the orientation of filter B and can observe the flashing light on box B. During an experiment, there is no way for Alice and Bob to communicate.
The Experiment:
The source is adjusted so it emits pairs of entangled electrons in approximately 5 second intervals. Alice randomly chooses one of the possible orientations (1, 2, or 3) of the left filter (A) before each electron arrives, and Bob randomly chooses one of the possible orientations of the right filter (B) before the companion electron arrives. The arrival of an electron triggers a light to flash. In a table Alice and Bob record the sequence of colors (green or red) of the flashes on their respective boxes. After a large number of flashes have been observed, the experiment is stopped and Alice and Bob are now allowed to communicate and compare their results.
How often did Alice and Bob obtain the same result, i.e. how often did they record the same color?
The orientation of each filter is chosen randomly. For each
filter, each orientation is chosen ~ 1/3 of the time. The larger the number
of trials, the less we expect the fraction Ni/Ntotal
to deviate from 1/3. (Ni = number of trial with orientation i =
1, or 2, or 3, Ntotal = total number of trials.)
(Link:
Rolling Dice:
The more often we roll, the more the distribution approaches the expected
distribution.)
For the two filters there are 9 possible combinations of orientations, each combination is equally likely and is chosen ~ 1/9 of the time.
Possible Combinations
|
|
|
Filter A |
||
|
|
Position |
1 |
2 |
3 |
|
Filter B |
1 |
1,1 |
1,2 |
1,3 |
|
2 |
2,1 |
2,2 |
2,3 |
|
|
3 |
3,1 |
3,2 |
3,3 |
|
If both filters have the same orientation, 1,1, or 2,2, or 3,3, then either both electrons will pass their through their respective filters, or both will hit a beam stop. The lights on the filters A and B will flash the same color.
For the other 6 combinations, 1,2, or 1,3, or 2,1, or
2,3, or 3,1 or 3,2, the probability that both lights flash the same
color is 1/4.
Let us take, for example, the combination 1,2. The right-filter axis
points down. If the light flashes green, then the right electron's spin
points down. Entanglement guaranties that the left electron's spin
points up. But axis 2 of the left filter is oriented 120o
away from the z-axis, so cos2(θ/2)
= cos2(60o) = 1/4 is the probability that this
electron will pass through its filter. 1/4 of the green flashes of
analyzer B will be accompanied by green flashes of analyzer A.
If, however, the light on the right filter box flashes red, then the right electron's spin points up and it hits the beam stop. Entanglement guaranties that the left electron's spin points down. But axis 2 of the left filter is oriented 60o away from the negative z-direction, so cos2(θ/2) = cos2(30o) = 3/4 is the probability that this electron will pass through its filter. Therefore 1/4 of the electrons will hit the beam stop, and 1/4 of the red flashes of filter B will be accompanied by red flashes of filter A.
We can analyze the combinations 1,3, or 2,1, or 2,3, or 3,1 or 3,2 in the same way. The probability that the lights on the filters A and B will flash the same color is always 1/4 for these combinations.
The total probability that both filters flash the same color therefore is
P(same color) = (1/9)*[1 + 1 + 1 + 1/4 + 1/4 + 1/4 + 1/4 +1/4 +1/4] = (1/9)*4.5 = 1/2.
For a large number of trials, ~50% of the time the lights on both filters will flash the same color. Experiments similar to the one described here have now been carried out many times and have always yielded this predicted result.
What is so special about that?
Quantum mechanics predicts incompatible observables for a
system. An observer cannot know the values of two incompatible observables of a
system at the same time. Does this mean that the system really does not have
well defined values for these observables before a measurement, or is it
possible that the system has well defined values, but these values are hidden
from the observer, and the observer just cannot obtain the complete information?
In 1964 J.S. Bell showed that the assumption of hidden variables is inconsistent
with the outcome of the above described experiment. If there were hidden
variables, we would have to observe the light flashing the same color more than
50% of the time. We will examine at a simple version of Bell's thought
experiment in an in-class activity.
Links:
J. S. Bell, On the Einstein Podolsky Rosen Paradox, Physics 1, 195 (1964)
J. S. Bell, On the problem of hidden variables in quantum mechanics, Rev. Mod. Phys. 38, 447 (1966)