

| In 1897 J. J. Thomson discovered the electron, a negatively charged particle more than two thousand times lighter than a hydrogen atom. In 1906 Thomson suggested that each atom contained a number of electrons roughly equal to its atomic number. Since atoms are neutral, the charge of these electrons must be balanced by some kind of positive charge. Thomson proposed a 'plum pudding' model, with positive and negative charge filling a sphere only one ten billionth of a meter across. This plum pudding model was generally accepted. Even Thomson's student Rutherford, who would later prove the model incorrect, believed in it at the time. |
|
| In 1911 Ernest Rutherford
proposed that each atom has a massive nucleus containing all of its
positive charge, and that the much lighter electrons are outside this
nucleus. The nucleus has a radius about ten to one hundred
thousand times smaller than the radius of the atom. Rutherford
arrived at this model by doing experiments. He scattered alpha
particles off fixed targets and observed some of them scattering through
very large angles. Scattering at large angles occurs when the
alpha particles come close to a nucleus. The reason that most
alpha particles are not scattered at all is that they are passing
through the relatively large 'gaps' between nuclei.
Links: The Rutherford Experiment |
 |
| Rutherford revised
Thomson's 'plum pudding' model, proposing that electrons orbit a
positively charged nucleus, like planets orbit a star. But
orbiting particles continuously accelerate, and accelerating charges
produce electromagnetic radiation. According to classical physics
the planetary atom cannot exist. Electrons quickly radiate away
their energy and spiral into the nucleus.
In 1915 Niels Bohr adapted Rutherford's model by saying that the orbits of the electrons were quantized, meaning that they could exist only at certain distances from the nucleus. Bohr proposed that electrons did not emit EM radiation when moving in those quantized orbits. |
|
Quantum mechanics now predicts what measurements can reveal about atoms. The hydrogen atom represents the simplest possible atom, since it consists of only one proton and one electron. The electron is bound, or confined. Its potential energy function U(r) expresses its electrostatic potential energy as a function of its distance r from the proton.
|
U(r) = -q2/(4πε0r) = -e2/r. Here e2 is defined as q2/(4πε0).
In SI unit 1/(4πε0) = 9*109
Nm2/C2, and q = 1.6*10-19
C.
|
 |
The energy levels in a hydrogen atom can be obtained by solving Schrödinger’s equation in three dimensions. We have to solve the radial equation
(-ħ2/(2m))∂2(rR))/∂r2 + (l(l + 1)ħ2/(2mr2))(rR) - (E - e2/r)(rR) = 0
or
∂2(rR))/∂r2
+ [(2m/ħ2)(E + e2/r) -
l(l + 1)/r2](rR)
= 0,
or
∂2(rR))/∂r2
+ k2(r)(rR) = 0,
with k2(r) = (2m/ħ2)(E + e2/r) - l(l + 1)/r2.
This equation can be integrated using the Numerov method. Click on the linked spreadsheet to find the allowed electron energies in the hydrogen atom numerically for states with zero angular momentum. All distance are measured in Å (10-10 m) and all energies in eV. (Note: We are solving the differential equation for the function rR(r), not for the function R(r).) Because we cannot integrate from infinity, the program assumes that rR(r) = 0 at r = 30Å. It integrates inward towards the origin. The radial functions R(r) have to be finite at the origin, and therefore the functions rR(r) have to be zero at the origin for a solution that fulfills the boundary conditions.
A spreadsheet macro increments the trial energies in small steps. When rR(0) changes sign the program records an eigenvalue. Only eigenvalues associated with radial functions, which rapidly decrease as r increases beyond a few Å, are physically reasonable solutions. Confinement leads to energy quantization.
The electron energies in the hydrogen atom do nor depend on the quantum numbers m and l which characterize the dependence of the wave function on the angles θ and φ. The allowed energies are
En = -me4/(2ħ2n2) = -13.6 eV/n2.
Here n is called the principle quantum number. The values En are the possible value for the total electron energy (kinetic and potential energy) in the hydrogen atom. The average potential energy is -me4/(ħ2n2) and the average kinetic energy is me4/(2ħ2n2).
The wave functions ψnlm(r,θ,φ) = Rnl(r)Ylm(θ,φ) are products of functions Rnl(r), which depend only on the coordinate r, and the spherical harmonics Ylm(θ,φ), which depend only on the angular coordinates. They are characterized by three quantum numbers, n, l, and m.
| The electron has three spatial
degrees of freedom. To completely determine its initial wave
function, we, in general, have to make three compatible measurements.
Some observables that are compatible with energy measurements and compatible with each other are
We can know the values of these observables labeled by n, l, and m, simultaneously. For the hydrogen atom, the energy levels only depend on the principal quantum number n. The energy levels are degenerate, meaning that the electron in the hydrogen atom can be in different states, with different wave functions, labeled by different quantum numbers, and still have the same energy. The electron wave functions however are different for every different set of quantum numbers.
Below is a link to plots of the square of the wave functions or the probability densities for the electron in the hydrogen atom for different sets of quantum numbers n, l, and m. Links: Note: Energy eigenfuctions characterize stationary state. We cannot track the electron and know its energy at the same time. If we know its energy, we can only predict probabilities for where we might find it if we tried to measure its position. If we determine the position of the electron, we lose the energy information.
|

Examples of hydrogen atom |
The probability of finding the electron in a small volume ∆V about the point (r,θ,φ) is |ψnlm(r,θ,φ)|2∆V. |ψnlm(r,θ,φ)|2 is the probability density, the probability per unit volume in three dimensions. |ψnlm(r,θ,φ)|2 is zero at the origin unless l = 0. But if l = 0, then the electron has zero orbital angular momentum, and there is a finite probability of finding it at the same position as the nucleus. |ψn00(r = 0)|2 is not equal to zero. This can lead to a special type of nuclear decay. Certain nuclei can de-excite by internal conversion, which is a process whereby the excitation energy is transferred directly to one of the atomic electrons, causing it to be ejected from the atom. This process competes with de-excitation by photon emission, which is called gamma decay. The probability of de-excitation by internal conversion is directly proportional to the probability of an electron being at the nucleus, and therefore only electrons with zero orbital angular momentum are involved.
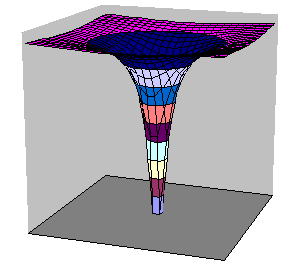
The hydrogen-atom wave function for n = 1, 2, and 3 are given below. The constant a0 appearing in these functions has the value a0 = 52.92 pm.

The probability of finding the electron in a small volume ∆V about the point (r,θ,φ) is |ψnlm(r,θ,φ)|2∆V. The probability of finding the electron whose wave function depends only on the coordinate r a distance r from the nucleus is |ψ(r)|2 4πr2∆r. [The volume ∆V a distance r from the nucleus is a spherical shell with radius r and thickness ∆r.] Only electrons in state with l = 0 have spherically symmetric wave functions.
Problem:
Find the probability per unit length of finding an electron in the ground state of hydrogen a distance r from the nucleus. At what value of r does this probability have its maximum value?
Solution:
Given the ground state wave function ψ100(r,θ,φ)
= ψ100(r)
= [1/(π1/2a03/2)]exp(-r/a0),
we find the probability per unit length,
P100(r) = |ψ100(r)|2
4πr2 = (4/a03)
r2 exp(-2r/a0). We can plot P100(r)
versus r. Let us measure r in units of a0. Open the
linked spreadsheet to view the plot.
The plot shows that P100(r) has its maximum value at r = 1 (in
units of a0), i.e at r = a0.
Suggestion: Change the spreadsheet to plot P200(r) = |ψ200(r)|2 4πr2 = (1(/4a03)) r2 (2 - r/a0)2exp(-r/a0). At what value of r does this probability have its maximum value? Note: Because we measuring distances in units of a0, a0 in units of a0 is equal to 1, and you need to plot P200(r) = (1/4) r2 (2 - r)2exp(-r).
Letters of the alphabet are associated with various values of l.
|
|
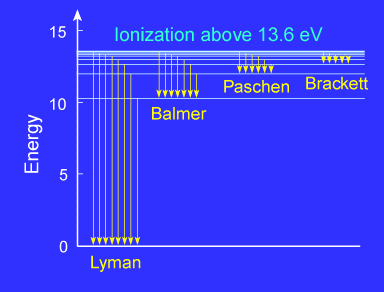
The hydrogen line spectrum:
| When an electron changes from one
energy level to another, the energy of the atom must change as well. It
requires energy to promote an electron from one energy level to a higher
one. This energy can be supplied by a photon whose energy E is
given in terms of its frequency E = hf or wavelength E = hc/λ.
Since the energy levels are quantized, only certain photon wavelengths can be absorbed. If a photon is absorbed, the electrons will be promoted to a higher energy level and will then fall back down into the lowest energy state (ground state) in a cascade of transitions. Each time the energy level of the electron changes, a photon will be emitted and the energy (wavelength) of the photon will be characteristic of the energy difference between the initial and final energy levels of the atom in the transition. The energy of the emitted photon is just the difference between the energy levels of the initial (ni) and final (nf ) states. The set of spectral lines for a given final state nf are generally close together. In the hydrogen atom they are given special names. The lines for which nf = 1 are called the Lyman series. These transitions frequencies correspond to spectral lines in the ultraviolet region of the electromagnetic spectrum. The lines for which nf = 2 are called the Balmer series and many of these spectral lines are visible. The spectrum of hydrogen is particularly important in astronomy because most of the Universe is made mostly of hydrogen. |
 |
|
| The Balmer series, which is the
only hydrogen series with lines in the visible region of the
electromagnetic spectrum, is shown in the right in more detail.
The Balmer lines are designated by H with a Greek subscript in order of decreasing wavelength. Thus the longest wavelength Balmer transition is designated H with a subscript alpha, the second longest H with a subscript beta, and so on.
|
 |
Problem:
What is the wavelength of the least energetic line in the Balmer series?
Solution:
The transition from ni = 3 to nf = 2
is the lowest energy, longest wavelength transition in the Balmer series.
∆E = -13.6 eV(1/9 - 1/4) = 1.89 eV =
3*10-19 J. λ = hc/∆E = 658
nm.
Problem:
What is the shortest wavelength in the Balmer series?
Solution
The transition from ni = ∞ to nf = 2
is the highest energy, shortest wavelength transition in the Balmer series.
∆E = -13.6 eV(1/∞ - 1/4) = 13.6/ 4 eV =
3.4 eV = 5,44*10-19 J. λ = hc/∆E
= 365 nm.
Hydrogenic atoms
Atoms with all but one electron removed are called hydrogenic atoms.
If the charge of the nucleus is Z times the proton charge, then U(r) = -Ze2/r.
The solutions to the Schroedinger equation of such atoms are obtained by simply scaling the the solutions for the hydrogen atom.
The energy levels scale with Z2, i.e. En = -Z2*13.6 eV/n2. It takes more energy to remove an electron from the nucleus, because the attractive force that must be overcome is stronger.
The average size of the wave functions scales as 1/Z, i.e. the electron, on average, stays closer to the nucleus, because the attraction is stronger. In the wave functions we replace a0 by a0/Z.
The Bohr Atom
In 1913 Bohr's model of the atom revolutionized atomic physics. The Bohr model consists of four principles:
| With these conditions Bohr was
able to explain the stability of atoms, as well as the emission spectrum
of hydrogen. According to Bohr's model only certain orbits were
allowed which means only certain energies are possible. These
energies naturally lead to the explanation of the hydrogen atom
spectrum. Bohr's model was so successful that he immediately received world-wide fame. Unfortunately, Bohr's model worked only for hydrogen and hydrogenic atoms, such as any atom with all but one electron removed. The Bohr model is easy to picture, but we now know that it is wrong. Any planetary model of the atom, so often seen in pictures and so easy to picture, is wrong. Links:
|
 |