

In-class group activity 11:
If two spin-1/2 particles are spin entangled, a single measurement of the component of one of the particle's the spin along any axis immediately determines the spin polarization of both particles. Quantum entanglement is the basis for emerging technologies such as quantum computing and quantum cryptography and has been used for experiments in quantum teleportation. At the same time, it produces some of the more theoretically and philosophically disturbing aspects of the quantum theory, as one can show that the correlations predicted by quantum mechanics are inconsistent with the seemingly obvious principle of local realism, which is that all objects have a well defined state, and information about that state should not be transferred instantaneously.
Reality: If without disturbing a system we can predict with certainty the value of a physical quantity, then there exists an element of physical reality corresponding to that quantity.
Locality: If two systems cannot interact with each other, then a measurement of one system cannot change the state of the other system.
The origin of this topic is a famous paper by Einstein, Rosen and Podolsky (EPR) in 1935. Its title is "Can Quantum-Mechanical Description of Physical Reality be Considered Complete?" The authors considered what Einstein called the "spooky action-at-a-distance" that seems to be part of Quantum Mechanics, and concluded that the theory must be incomplete if not outright wrong. Einstein never did accept Quantum Mechanics. One of his objections was that "God does not play at dice with the universe." Bohr responded: "Quit telling God what to do!"
In the early 1950's David Bohm was a young Physics professor at Princeton University. He was assigned to teach Quantum Mechanics and, as is common, decided to write a textbook on the topic. The book is still a classic. Einstein was at Princeton at this time, and as Bohm finished each chapter of the book, Einstein would critique it. By the time Bohm had finished the book Einstein had convinced him that Quantum Mechanics was at least incomplete. Bohm then spent many years in search of hidden variables, unobserved factors inside, say, a radioactive atom that determines when it is going to decay. In a hidden variable theory, the time for the decay to occur is not random, although the variable controlling the process is hidden from us.
In 1964 J.S. Bell showed that the assumption of hidden variables can have observable consequences. If there were hidden variables the outcome of certain experiments, such as those using entangles spins and spin analyzers, would have to be different than the outcome predicted by quantum mechanics. But the predictions of quantum mechanics have been checked and found to be correct. They do not satisfy Bell's inequality or Bell's theorem for a theory that includes hidden variables. Quantum mechanics is non-local.
Does this non-locality allow for instantaneous communication? No!
A measurement of the spin-polarization state of one of the particles of a spin-entangled pair instantaneously determines the spin-polarization state of the other particle, independent of their separation. “The observer” instantaneously has information about the polarization state of both particles. But “the observer” (Alice, Bob, and the rest of the world) has to process the information consistent with the “laws of physic”. Quantum mechanics is non-local in a way that does not allow superluminal communication.
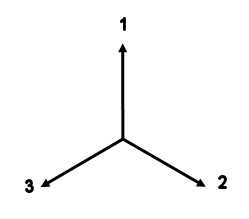
Let us look at a simple version of Bell's thought experiment. The experimental apparatus is the same as described in the previous section. We have a source that emits a pair of electrons. The source is placed between two detectors, A and B. The detectors are mounted in boxes, and there are 3 different orientations for each detector inside each box, labeled 1, 2, and 3. The box which contains the right detector is rotated by 180o with respect to the box which contains the left detector. The source and the two detectors are not connected in any way and can be separated by very large distances. When an electron enters a detector, a light on the box flashes either green or red. Alice and Bob can choose the orientations of the detectors and observe and record the colors of the flashing lights and the orientations of the detectors.
| A | B | |
 |
 |
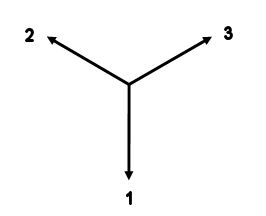 |
Alice and Bob believe in local realisms, i.e. they believe that the electrons have well defined properties when they leave the source. They believe that for a given orientation of the detector the color of a flash is determined by a real physical property of the electron. Investigating further, for example by placing a second detector in the same orientation at variable distances behind the first one and always observing it to flash the same color as the first one, they conclude that this physical property does not change with time. Placing a second detector in a different orientation behind the first one, they find that this second detector sometimes flashes the same and sometimes flashes a different color. The second detector must therefore measure a different property of the electron. Alice and Bob conclude that the three different orientations of the detectors measure three different properties of the electrons.
The condition of an electron as far as these properties are concerned can therefore be described by the following the eight labels (R = red, G = green)
RRR, RRG, RGR, GRR, RGG, GRG, GGR, GGG.
The electron makes the light flash the color indicated by the first of the three letters if the detector has orientation 1, the color indicated by the second letter if the detector has orientation 2, and the color indicated by the third letter if the detector has orientation 3. An electron in the state RRG, for example, will always cause the light on the detectors in orientation 1 and 2 to flash red, and the light on the detector in orientation 3 to flash green.
During an experiment Alice randomly chooses one of the possible orientations of the left detector (A) before each electron arrives and Bob randomly chooses on of the possible orientations of the right detector (B) before the companion electron arrives. The arrival of an electron triggers a light to flash. In a table Alice and Bob record the sequence of colors (green or red) of the flashes on their respective detector boxes. After a large number of flashes has been observed, the experiment is stopped and Alice and Bob are now allowed to communicate and compare their results.
There are 9 possible combinations of orientations.
Possible Combinations
|
|
|
Detector A |
||
|
|
Position |
1 |
2 |
3 |
|
Detector B |
1 |
1,1 |
1,2 |
1,3 |
|
2 |
2,1 |
2,2 |
2,3 |
|
|
3 |
3,1 |
3,2 |
3,3 |
|
Alice and Bob observe that if they choose the combinations 1,1, or 2,2, or 3,3, then the lights on the detectors A and B always flash the same color. They conclude that the electrons are always created with identical properties in the source. (Actually they are created with 100% correlated properties, which do not have to be identical, since the boxes are rotated 180o with respect to each other.)
Alice and Bob now make a table, into which they enter their predictions of same or different color flashes for the various emission conditions and switch combinations.
|
|
Switch Combination |
||||||||
|
emission |
1,1 |
2,2 |
3,3 |
1,2 |
1,3 |
2,1 |
2,3 |
3,1 |
3,2 |
|
RRR |
same |
same |
same |
same |
same |
same |
same |
same |
same |
|
RRG |
same |
same |
same |
same |
different |
same |
different |
different |
different |
|
RGR |
same |
same |
same |
|
|
|
|
|
|
|
GRR |
same |
same |
same |
|
|
|
|
|
|
|
RGG |
same |
same |
same |
|
|
|
|
|
|
|
GRG |
same |
same |
same |
|
|
|
|
|
|
|
GGR |
same |
same |
same |
|
|
|
|
|
|
|
GGG |
same |
same |
same |
|
|
|
|
|
|
Activity: Please complete this table. Then, using your results, construct a table which lists the probability of obtaining flashes of the same color for each emission condition.
|
emission |
Probability of obtaining flashes |
|
RRR |
1 |
|
RRG |
5/9 |
|
RGR |
|
|
GRR |
|
|
RGG |
|
|
GRG |
|
|
GGR |
|
|
GGG |
|
Alice and Bob may not know the distributions of the eight emission conditions produced by the source. (For example, it is possible that the source produces only one of the emission conditions, or that it produces all eight emission conditions with equal probabilities of 1/8.) They can therefore not predict the exact probability of obtaining flashes of the same color. But they can put a lower limit on this probability.
What is this lower limit? Is it add odds with the measurement described in the previous section?
References:.