Macro- and microstatess

In-class group activity 14:

Discuss and answer all questions (blue font color).

Open a Microsoft Word document to keep a log of your  results and discussions.

(a) Assume 50 students registered for a course.  You need to report the total number of students who actually attend.  You have every student in attendance sign a list.

(b) Consider the following macrostates of the class.

  1. All 50 students are present.
  2. 25 students are present.
  3. 1 student is present.
  4. No students are present.
(c) Assume you have two boxes and you have to place a coin into each box.  You toss a coin and place it into box 1 without changing its orientation.  The side of the coin facing up can be either head (blue) or tail (red).  Then you toss a second coin and place it into box 2 without changing its orientation.  There are 4 different microstates.  You are interested in the different configurations, ie e. you are interested in how many coins end up "head up" or blue.
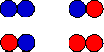(d) Now assume that you have a 6 by 6 array of squares.  You number the squares from 1 to 36.  You toss a coin and place it onto square 1 without changing its orientation.  The side of the coin facing up can be either head (blue) or tail (red).  You keep tossing coins and placing them in succession onto squares 2 through 36 without changing their orientation.  Each square holds exactly one coin.  (The macrostate is 36 coins on 38 squares.)
To specify the microstate of the array after you finished this process you have to list the color of each square.  Many different patterns (microstates) are possible, such as the ones shown on the right.  Every particular pattern is equally likely to occur.  There are 236 = 6.87*1010 possible patterns and the probability of observing any particular pattern is 1/236 = 1.46*10-11.
Suppose you are only interested in the configuration, i.e. you are only interested in how many squares are blue.  Most configurations correspond to many microstates.  A few of the allowed microstate for the “15 blue squares” configuration are shown on the right.

How many microstates are there for a given configuration?   This is the common problem of splitting a group of N into two smaller groups, of n and N - n, without caring about the ordering in each group.  The number of ways of doing it is N!/[n!(N-n)!].

Assume you have N colored objects, but n of them are “special”.  They could, for example be blue, while the other N - n objects are not blue (red).  There are N*(N - 1)*(N - 2)*…*2*1 = N! ways of distributing the n blue and N - n red objects over N places.  [For the first object you have N choices.  But now one place is occupied.  For the next object you only have N - 1 choices, etc.]  But for each of these distributions there are n! ways of arranging the blue objects among themselves without changing the pattern, and there are (N - n)! ways of arranging the other (red) objects among themselves without changing the pattern.  Therefore the number of distinct patterns you can produce is N!/[n!(N-n)!].

In our example N = 36.  If n = 15 there are 5.56*109 distinct patterns that have 15 blue squares.  There are 5.56*109 distinct microstates for the n = 15 configuration.  If n = 10, there are only 2.54*108 distinct patterns.  The n = 18 configuration has the maximum number of microstates, namely 9.08*108.  Since every microstate is equally likely and the total number of microstates is 2N,  the probability of observing a given configuration (n out of N)  is N!/[2Nn!(N-n)!].

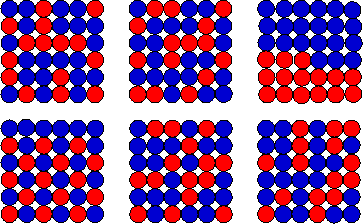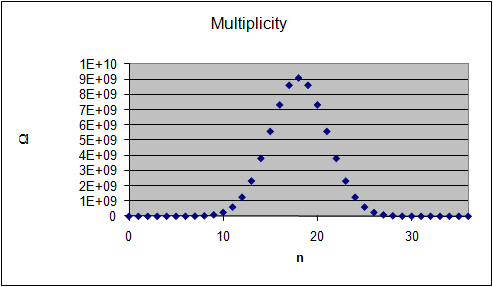
The graphs on the right show the multiplicity Ω for each "n out of 36" configurations and the probability of observing this configuration.  (See the attached spreadsheet.)  The probability of observing a configuration n <7 or n > 30 is practically zero.

Answer the multiple choice question below:

If we examine the probabilities for all of the configurations in the system we find that the probability is

  1. spread evenly among all of the configurations.
  2. spread out among a large fraction of the configurations, but with some configurations having slightly higher probabilities than others.
  3. concentrated within a small fraction of the configurations centered on the most probable configuration.
  4. entirely concentrated into the single most probable configuration.

How does this behavior scale with the number of coins N?

  • If you have N squares and N coins, the most probable number "head up" coins is N/2.  The spread of the distribution increases a N1/2, so the percentage spread decreases as N-1/2.
  • For 36 square, the spread approximately plus or minus 6, the percentage spreads is (1/6)*100% or 16.6%.  That means that if n differs by more than 16.6% from 18, then it is not very likely to occur.
  • If there were N = 1024 squares and coins (just as there might be 1024 molecules in a gas), then the percentage spread is (10-12)*100% = 10-10%.  This means that if n differs from N/2 or 0.5*1024 by more than 10-10%, it is not very likely to occur.

As the number of particles grows, the probability of observing the most likely configuration becomes nearly indistinguishable from 1.

 

(